Комплексный подход к оценке экономического неравенства населения



В данной статье рассмотрены подходы к оценке экономического неравенства населения отечественными и зарубежными учеными и экономистами.

Ключевые слова: экономическое неравенство населения, кривая Лоренца, индекс Джини, коэффициент фондов.

Начальным этапом количественной оценки степени дифференциации населения (индивидов, домашних хозяйств) по уровню доходов является их распределение по величине среднедушевых денежных доходов. При проведении оценки неравенства благосостояния населения исходными данными выступают результаты выборочных статистических наблюдений.

В ходе анализа микроданных таких обследований строится эмпирический ряд распределения, который ставит в соответствие каждому значению доходов, встречающемуся в выборке, долю населения с душевым доходом, не превышающим этот уровень, в общей численности выборки. Затем происходит обобщение результатов выборочного наблюдения на генеральную совокупность (население региона) и строятся интервальные ряды распределения доходов.

Выделяют три типа рядов — децильные (разбивающие всю совокупность на 10 равных интервалов по 10 % единиц наблюдения в каждом интервале), квантильные (дробящие совокупность на 5 интервалов по 20 % единиц) и интервалы с заданными (фиксированными) границами уровней дохода и численности населения и домохозяйств в них. Интервальные ряды распределения доходов являются основой для таких базовых инструментов в анализе неравенства доходов как кривая Лоренца и коэффициент Джини.

Графически функция распределения доходов населения может быть представлена путем построения кривой Лоренца, предложенной американским экономистом и социологом М. Лоренцем в 1905 году в работе «Метод измерения концентрации доходов». Для построения кривой по оси абсцисс отражается кумулятивное распределение населения по мере возрастания среднедушевого дохода в общей численности населения региона, а по оси ординат откладываются соответствующие накопленные доли доходов. Графически кривая Лоренца представлена на рисунке 1.

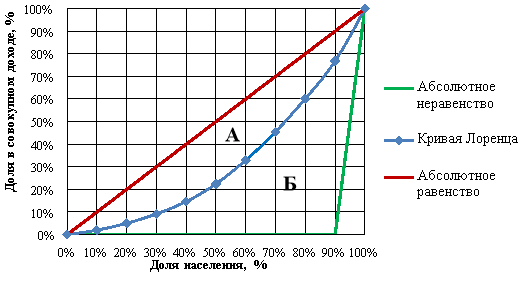
Рис. 1. Кривая Лоренца [1, с. 176]

Каждая точка на кривой Лоренца показывает, какую долю совокупного дохода получает определенная доля населения. В том случае, когда каждой доле населения соответствует равная ей доля в общем объеме совокупного дохода, возникает абсолютное равенство населения по уровню доходов. На графике абсолютное равенство представлено биссектрисой, проведенной из начала координат. При неравномерном распределении кривая Лоренца отклоняется от линии абсолютного равенства и представляет собой выпуклую вниз кривую. Таким образом, чем ближе эмпирическая кривая Лоренца расположена к биссектрисе, тем равномернее в обществе распределены доходы, следовательно, тем меньше неравенство, и наоборот — чем дальше кривая Лоренца расположена от прямой линии равномерного распределения, тем больше уровень дифференциации населения по уровню доходов. В том случае, когда 10 процентам населения принадлежит весь совокупный доход, возникает абсолютное неравенство [1]. Такая ситуация в обществе графически может быть представлена кривой абсолютного неравенства, изображенной на рисунке 1.

Кривая Лоренца выступает наглядным инструментом, позволяющим сопоставить данные о распределении доходов населения в каждой точке накопленных долей, однако на практике такой инструмент оценки степени дифференциации населения по уровню доходов не позволяет количественно оценить неравенство. Этот недостаток кривой Лоренца может быть устранен путем расчета индекса Джини.

Индекс концентрации доходов или Индекс Джини (G) был впервые предложен в 1912 году итальянским статистиком, социологом, демографом и экономистом Коррадо Джини. Основное назначение индекса — количественная оценка распределения совокупной величины доходов между отдельными группами населения. Значение индекса Джини может варьироваться от 0 до 1: чем ближе коэффициент к единице, тем выше неравенство в распределении доходов, и наоборот — чем меньше данный коэффициент, тем равномернее распределены доходы [2]. В том случае, если коэффициент Джини равен нулю, то в обществе наблюдается абсолютное равенство, при коэффициенте равном единице — абсолютное неравенство.

Геометрический смысл коэффициента Джини заключается в том, что он представляет собой отношение площади фигуры, расположенной между линией абсолютного равенства и кривой Лоренца S_A (область «А» на рисунке 1), к площади всего треугольника, расположенного под линией абсолютного равенства S_А+Б (область «А+Б» на рисунке 1) [2]. В данном случае для расчета коэффициента Джини может быть применена формула 1.

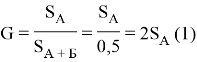
Согласно Методике расчета показателей распределения и дифференциации по уровню доходов населения, представленной Федеральной службой государственной статистики Российской Федерации, коэффициент Джини может быть рассчитан по формуле 2.

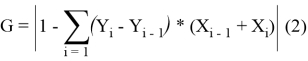
Где

Y_i -Y_i-1 — доля населения, относящаяся к i-му интервалу;

X_i+1, X_i — доля суммарного дохода, приходящаяся на начало и конец i-го интервала.

Помимо представленной выше методики, в настоящее время в экономической отечественной и зарубежной литературе исследователями представлены иные подходы к расчету индекса Джини.

В 1984 г. израильскими экономистами Р. Лерманом и Ш. Ицхаки была представлена методика расчета коэффициента Джини, которая позволила количественно оценить степень дифференциации доходов без оценки плотности распределения населения по уровню доходов. Для этого было предложено все исходные данные о доходах населения региона упорядочить по мере возрастания и каждому значению дохода присвоить ранг. Следует отметить, что по рассматриваемой методике индивиду (домохозяйству), имеющему наименьшую величину дохода, присваивается ранг, равный 1, а индивиду (домохозяйству) с наибольшим доходом ранг n, где n — общее число наблюдений (исследуемых индивидов, домохозяйств) [5]. Расчет коэффициента Джини по методике Р. Лермана и Ш. Ицхаки осуществляется по формуле 3.

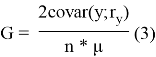
Где

y — величина дохода индивида (домохозяйства);

r_{y —} ранг дохода индивида (домохозяйства).

В 1997 году британско-американский экономист и академик Ангус Дитон в работе «Анализ обследований домашних хозяйств» представил методику расчета коэффициента Джини, в основе которой также был положен принцип ранжирования доходов. Однако по методике А. Дитона индивиду (домохозяйству), имеющему наибольшую величину дохода, присваивается ранг, равный 1, а индивиду (домохозяйству) с наименьшим среднедушевым доходом ранг n, где n — общее число наблюдений (исследуемых индивидов, домохозяйств). Данный подход позволил придать больший вес в выборке индивидам (домохозяйствам) с низким уровнем доходов [4]. Расчет коэффициента Джини по методике А. Дитона осуществляется по формуле 4.

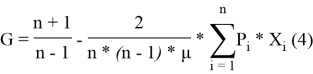
Где

x_{i —} упорядоченные по возрастанию значения доходов в выборке, где

x_i ≤ x_i+1, i ∈ [1;n];

р_i — ранг дохода индивида (домохозяйства) i.

Сербско-американский экономист, специалист по неравенству доходов и глобализации Бранко Миланович в 1997 году в работе «Простой способ расчета коэффициента Джини, а также некоторые последствия» обобщил существующие подходы и предложил производить расчёт коэффициента Джини с помощью коэффициентов вариации и корреляции. Ранг дохода в рамках данного подхода определяется аналогично методике расчета ранга

Р. Лермана и Ш. Ицхаки [5]. Расчет коэффициента Джини по методике

Б. Милановича осуществляется по формуле 5.

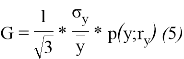
Где

σ_y — стандартное отклонение доходов индивидов (домохозяйств);

р (y; r_y) — коэффициент корреляции между доходами и рангом индивидов (домохозяйств);

r_{y —} ранг дохода индивида (домохозяйства).

Наряду с индексом Джини базовым инструментом оценки степени неравенства населения по уровню благосостояния вступает показатель превышения доходов 10 % населения, имеющего самые высокие доходы (S₁₀), над суммарными доходами 10 % населения с самыми низкими доходами (S₁) — коэффициент фондов (K_f). Основой для расчета коэффициента выступают децильные ряды, разбивающие всю исследуемую совокупность на 10 равных интервалов по 10 % единиц наблюдения в каждом интервале [1]. Коэффициент фондов может быть рассчитан по формуле 6.

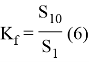
Таким образом, в настоящее время существует множество подходов к оценке уровня социально-экономического неравенства населения, что позволяет снизить погрешность при проведении расчетов и повысить надежность и точность результатов.

Литература:

1. Аникина, Е. А. Экономическая теория: учебник. — Томск: Изд-во Томского политехнического университета, 2014. — 413 с.
2. Костылева Л. В. Социально-экономическое неравенство населения региона: учеб. пособие / Л. В. Костылева, К. А. Гулин, Р. В. Дубиничев. — Вологда: ИСЭРТ РАН, 2009.
3. Жаромский, В. С. Социально-экономическое неравенство в России: динамика и методы оценки / В. С. Жаромский, Л. А. Мигранова, М. С. Токсанбаева // Народонаселение. — 2018. — № 4(21). — С. 79–95.
4. Deaton A. The Analysis of Household Surveys. — The John Hopkins University Press, Baltimore and London, 1997, 344 с.
5. Milanovic B. A simple way to calculate the Gini coefficient, and some implications. — Economics Letters 56, World Bank, Washington, D.C., USA, 1997, 115 с.