В статье рассматривается возможность моделирования ДНК и белков с помощью потенциала, сосредоточенного на кривых, для предсказания возможного переключения макромолекулы.
Ключевые слова: мат. моделирование, теория операторов
Белки и ДНК — это макромолекулы, которые являются очень длинными цепочками из аминокислот (в случае белков) или нуклеотидов (в случае ДНК), но чаще они встречаются в клетках, диаметр которых в сотни, а то и тысячи раз меньше длины цепочки, поэтому они свернуты в клубки и упакованы в относительно небольшом пространстве, как факт. Это значит, что зачастую большое количество частей молекул — этих самых цепочек — находятся очень близко друг к другу. Из-за этого есть ненулевая вероятность изменения цепочки макромолекулы, которое может привести к генетическим изменениям, или заболеванием живого существа, или другим нарушениям. Можно использовать потенциал, сосредоточенный на кривой в трехмерном пространстве в качестве модели такой макромолекулы. С такой точки зрения, соединение между различными частями кривой может привести к возникновению собственных состояний, появление которых, может стать причиной изменения молекулы. Это стимулирует наш интерес к собственным значениям в такой модели.
Положим кривую Γ в R3. Она определена функцией γ(s): R → R3. Пусть γ ∈ C1 везде и γ ∈ C2 кусочно-задана. Более того, сделаем кривизну не такой сильной, скажем, что существует константа C такая, что для всех s1,s2, имеет место неравенство |γ(s1) − γ(s2)| ≥ c|s1 − s2|. Давайте зададим смещенную кривую Γr. Для этих целей введем трехгранник Френе для Γ, т. е. тройку (t(s), b(s), n(s)) касательный, нормальный и бинормальный вектора, которые являются непрерывными функциями от s. Для заданных ξ,η ∈ R мы определим Γr следующим образом:
Γr = {γr(s) = γ(s) + ξb(s) + ηn(s), r = (ξ2 + η2)1/2.}
Существует некоторая r0, такая что Γ![]() выполняется для каждого r ≤ r0.
выполняется для каждого r ≤ r0.
Каждый функция f ∈ Hloc2 (R3 \ Γ) непрерывна на R3 \ Γ. Следовательно, ограничение на f на Γr, r < r0, однозначно определено. Обозначим его как fΓr(s). Это ограничение может быть рассмотрено как распределение из D0(R) с параметром
r. Определим самосопряженный оператор −∆Γ,β следующим образом
Функция f, f ∈ Hloc2 (R3\Γ)∩L2(R3) принадлежит D(−∆Γ,β), если
1)Следующие пределы [1]
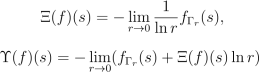 ,
,
существует почти везде в R, не зависят от направления ![]() , и определяют функцию из L2(R3);
, и определяют функцию из L2(R3);
2)Следующее равенство имеет место:
βΞ(f)(s) = Υ(f)(s).
Оператор действует как Лапласиан для x ∈ R3 \ Γ:
−∆Γ,β = −∆f.
Предлагается использовать частный случая кривых линий. А именно, пусть кривые Γ1,Γ2 в R3 имеют следующие выражения в картезианских координатах:
Γ1: γ1(s) = (s, 0, 0),Γ2:γ2(s) = (s cosθ, s sinθ, L),
s ∈ R, −π/2 < θ ≤ π/2.
Существенным спектром оператора −∆β = −∆Γ,β является следующее
![]()
Можно показать это, используя декомпозицию Нейманна [2]
Число−4e2(−β+ψ(1)) определяет собственное значение двухмерной системы одноточечного взаимодействия.
Нас интересует Гамильтониан, соответствующий потенциалу между двумя кривыми линиями.
Давайте получим спектральные уравнения. Собственная функция имеет вид
![]()
Чтобы выполнялись ограничения, описанные выше, нужно задать Ξ,Υ. Для этого удобно переписать u(x) в другой форме:
![]() (4)
(4)
Где ![]() — какое-то значение спектрального параметра, возьмем
— какое-то значение спектрального параметра, возьмем![]()
Теперь можем выразить Ξ1,Ξ2 остальное выразим через Υ1,Υ2:
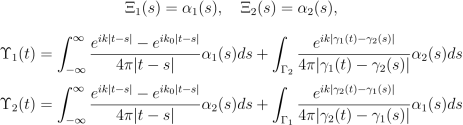
Преобразуя, получим интегральные уравнения для α1, α2:
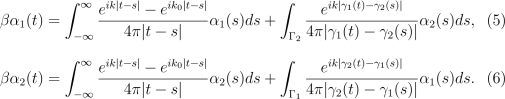
√![]()
Где |γ2(t) − γ1(s)| = s2 + t2–2 st cosθ + L2.
Таким образом, мы получили модель, которую хотели.
Литература:
- J.Brasche, P.Exner, Yu.A.Kuperin, P.Seba. Schr¨odinger operator with sigular interactions, J. Math. Anal. Appl., 184 (1994), 112–139.
- P. Exner, K. Nemcova: Bound states in point-interaction star graphs J. Phys. A34 (2001), 7783–7794

