В статье предложены формулы для определения влиянии инерционных сил на фильтрацию флюидов, при нелинейном законе фильтрации. Проявление этих сил связано с увеличением скорости фильтрации и направлены против движения и должны быть дополнительно преодолены. Получен аналитический вид для их определения, который позволяет количественно оценить влияние инерционных сил на дебит скважин.
Ключевые слова: давление, депрессия, фильтрация, нелинейный, инерция.
The article offers formulas for determining the effect of inertial forces on fluid filtration under the nonlinear filtration law. The manifestation of these forces is associated with an increase in the filtration rate and are directed against the movement and must be further overcome. An analytical view was obtained for their determination, which allows us to quantify the effect of inertial forces on the flow rate of wells.
Key words: pressure, depression, filtration, nonlinear, inertia.
При разработке залежей при больших градиентах давления на фильтрацию жидкости в пористой среде влияют инерционные силы, которые создают дополнительные сопротивления, направленные против движения. Таким образом, при больших скоростях течения природа нелинейности закона фильтрации иная, чем при малых скоростях фильтрации. А также с увеличением скорости движения время прохождения через сужение уменьшается, и жидкие частицы не успевают деформироваться. Это приводит к увеличению сопротивления движения [1, 2, 3.
В работе определяется давление, которое образуется в связи с влиянием инерционных сил. Как известно, закон Дарси представляется в виде 
, а двучленный закон фильтрации имеет вид [4]:
(1)
Здесь
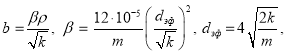(2)
в котором значение b определяется по данным Е. М. Минского [5].
В выражении (2)
– плотность жидкости, m — пористость породы, d — диаметр зерен, составляющий породу.
С увеличением скорости значение в формуле (1) члена 
не только становится соизмеримо с членом 
но и становится намного больше. В связи с чем полученное значение скорости фильтрации оказывается меньше, чем по закону Дарси, то есть для скорости фильтрации можно написать следующее выражение:
(3)
Здесь 
— градиент давления, который направлен против движения и связан с влиянием инерционных сил.
После некоторых преобразований из (1) действительно можно получить формулу (3), где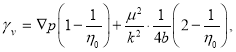 
(4)
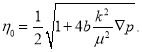(5)
Как видно, градиент инерционного давления 
прямо пропорционален 
и обратно пропорционален коэффициенту проницаемости k.
Можно показать, что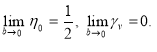 
Следует также отметить, что с уменьшением скорости фильтрации при двучленном законе фильтрации уменьшается и дебит скважины. Если при линейном законе фильтрации для дебита нефти существует обобщенная формула Дюпюи в виде [4]:
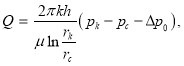(6)
то при двучленном законе можно эти формулы представить в виде:
для нефти —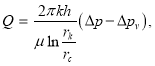
(7)
где 
Здесь 
– давление, которое направлено против движения и связано с влиянием инерционных сил.
Как известно [1] для дебита нефти с учетом начального градиента эта формула имеет следующий вид:
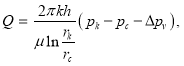
где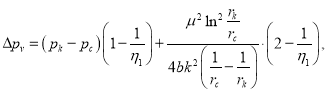 
(8)
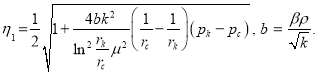
Как известно, в 1901 г. Форхгеймер, ссылаясь на исследования Мазони, рекомендовал выражать зависимость градиента давления от скорости (при больших градиентах) формулой:
где а и b — эмпирические коэффициенты. Однако ученый отметил, что еще лучше зависимость 
от 
будет выражаться трехчленным законом:
где с — эмпирический коэффициент.
Трехчленный закон фильтрации можно представить следующим образом [9]:
(9)
Здесь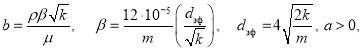 
Решая уравнение (1) по формуле Кардано после некоторых преобразование получаем следующее выражение для дебита:
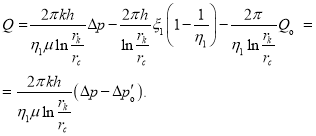(10)
Здесь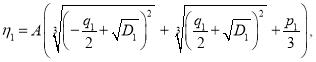 
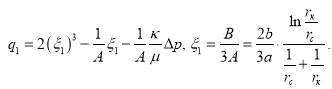
(11)
Формулу (10) можно представить в виде:
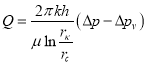, где 
(12)
Учитывая, что
то из формулы (10) получается формула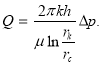 
А теперь выразим нелинейный закон фильтрации в экспоненциальном виде:
Предположим, что фильтрация в пласте происходит по линейному закону Дарси 
Однако под влиянием начального градиента и инерционных сил скорость уменьшается по экспоненциальному закону: 
— начальное пластовое давление. Учитывая, что при установившемся режиме фильтрации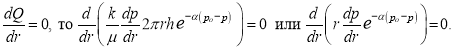 
Решая последнее уравнение, мы получаем:
При 
(13)
При 
(14)
Вычитая из уравнения (14) уравнение (13), получаем:
откуда
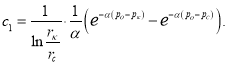(15)
Подставляя (15) в (13), получаем:
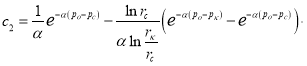(16)
Подставляя (15) и (16) в
, получаем:
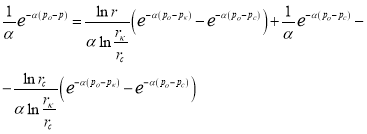
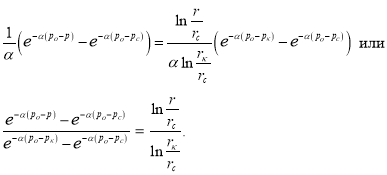
При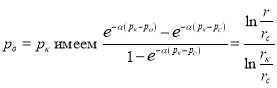 
или 
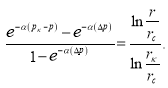(17)
Как видим, распределение давления имеет следующий вид:
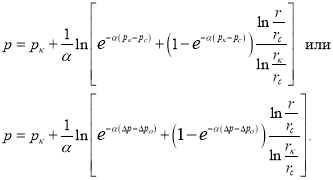(18)
Тогда для дебита после несложных преобразований, получаем:
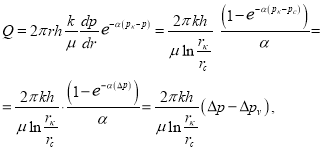
где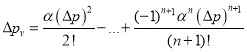 
(19)
Общее уравнение нелинейной фильтрации флюида для больших скоростей может быть представлено также в виде [8]:
(20)
Здесь основная трудность заключается в правильном нахождении коэффициентов
по данным гидрогазодинамических исследований.
В связи с этим предлагается следующая методика.
Для этого сначала получим некоторые необходимые формулы. Используя формулу (20) и обобщенный закон Дарси, можно записать:
(21)
Учитывая, что в этой формуле 
, (22)
то получаем:
(23)
Интегрируя правую часть выражения от 
а левую часть от 
получаем:
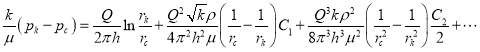(24)
Так как, 
1 где, i =1, n то этими выражениями можно пренебречь. Разделив обе части выражения на 
и применяя формулы (22), получаем:
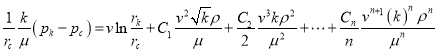
или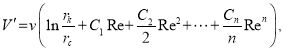
(25)
где 
Из формулы (25) можно получить:
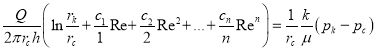(26)
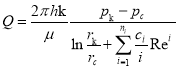(27)
Формулу (27) представим в виде обобщенной формулы Дюпюи:
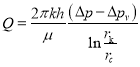(28)
где 
Предположим
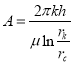(29)
Тогда используя формулы (27) и (28) получим:
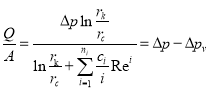(30)
или
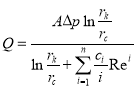(31)
Из формулы (30) также можно написать:
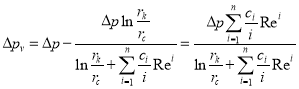(32)
С другой стороны из (28) и (29) получаем:
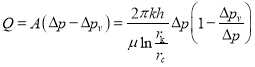(33)
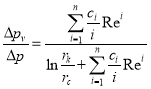(34)
Коэффициенты 
определяются по данным гидрогазодинамических исследований скважин при установившихся режимах фильтрации.
При 
из (33) получается формула Дюпюи:
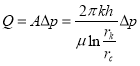(35)
С другой стороны из (19) получается также обобщенная формула Дарси:
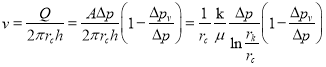(36)
Где 
находится из (34).
Таким образом, формулы (33), (34) и (36) являются новыми обобщенными формулами Дюпюи и Дарси.
Следовательно, в работе предложены различные формулы для определения влияния инерционных сил на фильтрацию флюидов, с учетом начального градиента при нелинейном законе фильтрации, связанные с увеличением скорости фильтрации и направленные против движения, которые должны быть дополнительно преодолены. Также получен аналитический вид для их определения, позволяющий количественно оценить влияние инерционных сил на дебит скважин.
Литература:
- Г. И. Баренблатт, В. М. Ентов, В. М. Рыжик. Теория нестационарной фильтрации жидкости и газа. — М.: Недра, 1972.
- А. Х. Мирзаджанзаде, О. Л. Кузнецов, Х. С. Басниев, З. С. Алиев. Основа технологии добычи газа. — М.: Недра, 2003. –880 с.
- А. Х. Мирзаджанзаде, И. М. Аметов, А. Г. Ковалев. Физика нефтяного и газового пласта. –Москва-Ижевск: Институт компьютерных исследований. –2005. –280 с.
- К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. Подземная гидравлика. –М.: Недра, 1986. — 303 с.
- Минский Е. М. О турбулентной фильтрации газа в пористых средах // Тр.ВНИИгаза. –М.: Гостоптехиздат, 1951. –С.64–71.
- И. Р. Гасанов., С. А. Таирова., Р. И. Гасанов. Методика интерпретации индикаторных линий скважин, добывающих углеводороды с аномальными свойствами. Научно-технический вестник. Каротажник — Выпуск 1 (271). Тверь — 2017.
- Спиридонов О. В. Расширенные возможности Microsoft Excel 2003 / О. В. Спиридонов. — Центр дистанционных образовательных технологий МИЭМП, 2010.
- И. Р. Гасанов, М. А. Джамалбеков. Обобщенная методика интерпретации данных гидрогазодинамических исследований при нелинейных законах фильтрации с учётом влияния начального градиента. Научно-методический журнал «Вестник науки и образования» 2020. No 3 (81). Часть 1. с.97–102.
- Т. Ш. Салаватов., И. Р. Гасанов. О трехчленном законе фильтрации, учитывающем влияние инерционных сил, начального градиента и неравновесность фильтрации. GEOPETROL Zakopane-Koscielisko 2018 Международная конференция 17–20 Сентября, с. 565–571.
