Статья посвящена описанию курса внеурочной деятельности по математике «Задачи с параметрами» для обучающихся основной школы.
Ключевые слова: внеурочная деятельность, задача, параметр, уравнение, решение, государственная итоговая аттестация.
Одним из требований Федерального государственного образовательного стандарта является реализация образовательной программы как в урочной, так и во внеурочной деятельности. Внеурочная деятельность по предмету может быть осуществлена в различной форме. На наш взгляд, элективный курс по определенному разделу математики — оптимальная форма реализации внеурочной деятельности. Целью курса является удовлетворение интеллектуальных потребностей обучающихся, поэтому его тематика курса определяется, как правило, запросами обучающихся.
Выбор темы курса внеурочной деятельности связан с включением задач с параметрами в содержание контрольно-измерительных материалов Государственной итоговой аттестации выпускников по математике (профильный уровень). Кроме того, специфика подобных задач заключается в их ярко выраженном нестандартном исследовательском характере. Тем самым определяется актуальность углубленного изучения именно данного раздела математики.
Определим основные понятия. В. В. Мирошин даёт следующие определение «параметра» и «задачи с параметрами»:
Параметром называется независимая переменная величина, входящая в условие задачи или появляющаяся в процессе её решения, «управляющая» решением задачи.
Задача, условие которой содержит или в ходе решения которой появляется хотя бы одна независимая переменная, удовлетворяющая определению понятия «параметр», называется задачей с параметрами [2, с. 19].
Классифицировать задачи с параметрами можно по различным основаниям, для этого имеется большое количество признаков. Так, например, Клейн предлагает основанием классификации число параметров.
Ю. М. Колягин рассматривает классификацию задач по сложности в зависимости от числа компонентов, являющихся неизвестными и придающими ситуации проблемный характер [1]. Он выделяет четыре типа задач: стандартные задачи, обучающие задачи, поисковые задачи и проблемные задачи. При этом сами задачи с параметрами классифицируются по следующим основаниям: по постановке задания; по теме; по методу; и по сложности.
Особенностью классификации задач по методу является то, что задача рассматривается в неразрывной связи с методом ее решения. Чаще всего рассматривают аналитические или графические (координатно-графический) методы. В основном многие задачи с параметрами могут быть решены как аналитически, так и графически, однако чаще всего используется синтез данных методов.
При подготовке к государственной итоговой аттестации данным методам и приемам нужно уделять пристальное внимание, что не всегда возможно сделать, ограничиваясь рамками обычного урока. Поэтому для качественной подготовки к решению подобных задач нужен специальный курс внеурочной деятельности, который необходимо начинать достаточно рано. Многие задачи с параметрами можно рассматривать с начала изучения систематического курса алгебры.
Спроектированный нами курс внеурочной деятельности по математике «Задачи с параметрами» предназначен учащимся 8–9 классов и направлен на развитие познавательного интереса и формирование исследовательских навыков, а также изучение приемов и методов решения задач повышенного уровня сложности. Целями курса внеурочной деятельности являются: формирование математического мышления учащихся через знакомство с приемами и методами решения задач с параметрами, развитие математической культуры школьников, а также повышение мотивации к самостоятельному изучению некоторых классов уравнений и неравенств с параметрами.
Остановимся подробнее на решении на решении некоторых задач с параметрами, доступными учащимся 8–9 классов:
Задача 1. Решить уравнение 
.
Преобразуем правую часть уравнения:
Контрольные значения параметра (термин А. Г. Мордковича) — те, которые обращают в 0 коэффициент при х в левой части. Таким значением является
При этом значении а и левая, и правая части обращаются в 0 и уравнение превращается в верное числовое равенство независимо от значения переменной х.
При
левую и правую части уравнения можно сократить на 
, тогда получаем единственное решение 
Таким образом, при 
уравнение имеет бесконечное число корней (любое действительное число является корнем данного уравнения); при 
уравнение имеет единственный корень
Задача 2. При каких значениях параметра а уравнение
имеет ровно три решения?
Корнями данного уравнения являются следующие значения переменной:
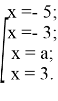
Уравнение имеет три различных корня в том и только том случае, когда значение параметра а совпадает с одним из чисел 
и 
. При всех других значениях параметра уравнение имеет четыре различных корня. Таким образом, уравнение имеет ровно четыре решения при
и ровно три решения при 
Таким образом, курс внеурочной деятельности по математике «Задачи с параметрами» представляет возможность не только для формирования умений и навыков учащихся, но и развития у них логического мышления, расширения математического кругозора, формирования математической культуры.
Литература:
- Колягин Ю. М. Задачи в обучении математике. Т. 1–2. — М.: Просвещение, 1977.
- Мирошин В. В. Существенные признаки понятия «параметр» // Математика в школе. — № 7. — 2010. — С. 19–22
- Мордкович А. Г. Беседы с учителями математики: Учеб.-метод. пособие. — М.: ООО «Оникс», 2008.
