В статье авторы предлагают аналитический аппарат расчета кинематической характеристики подвески на примере подвески с двумя неравными поперечными рычагами.
Ключевые слова: подвеска колесных транспортных средств, аналитический расчет, кинематическая характеристика.
Для создания математических моделей транспортных средств, как колебательных систем, необходимо в любой момент времени знать положение упругих элементов подвески в зависимости от перемещения колеса, то есть иметь кинематическую характеристику подвески.
В ряде случаев кинематическая схема подвески транспортного средства достаточна сложна, особенно у базовых машин высокой проходимости и грузоподъемности, поэтому кинематическую характеристику их подвесок получают, как правило, графическим путем [1, 2]. Строя в масштабе ряд положений подвески, определяют вертикальные перемещения оси колеса и соответствующие им деформации упругого элемента подвески. Однако графические построения громоздки, а также возникают трудности с использованием полученной кинематической характеристики в математических моделях. В этой связи возникает необходимость в разработке аналитического аппарата расчета кинематической характеристики подвески.
Предлагается следующая методика разработки этого аппарата.
Выбирают параметр, величина которого изменяется в процессе работы подвески, удобный для вывода уравнений связи. Это, например, может быть угол 
(см. Рис. 1). Затем получают уравнения связи перемещения упругого элемента 
и хода колеса h в функции от выбранного параметра:
, (1)
. (2)
По выражениям (1) и (2) появляется возможность построения кинематической характеристики подвески, то есть зависимости:
. (3)
При решении задач динамики транспортных средств необходимо иметь зависимость изменения перемещения упругого элемента при изменении хода колеса на некоторую величину.
Выражения для изменения перемещения упругого элемента 
и хода колеса 
при изменении угла 
на величину 
запишем в виде:
, (4)
, (5)
где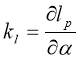 
, 
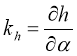— коэффициенты влияния.
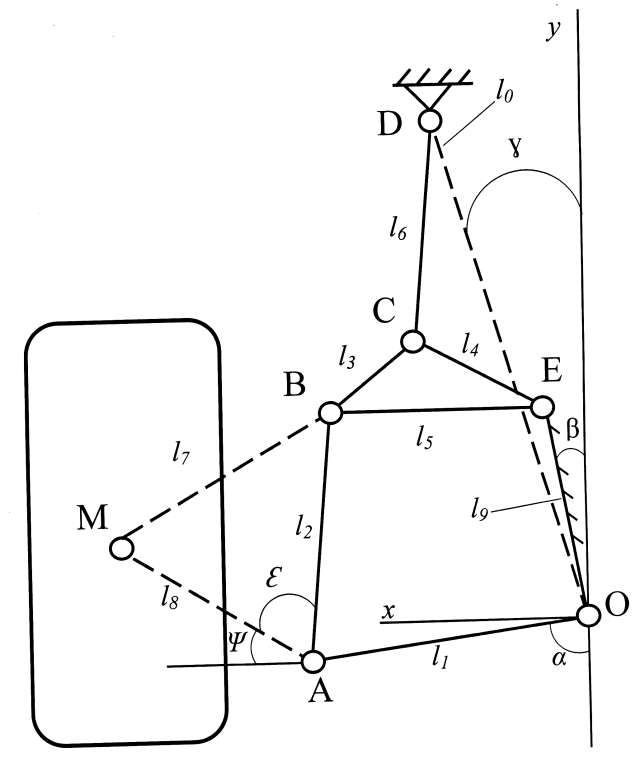
Рис. 1. Кинематическая схема подвески
Изменение хода упругого элемента при изменении хода колеса определяется выражением:
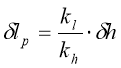. (6)
Следующим шагом методики является получение зависимостей для коэффициентов влияния 
и 
.
Выражение (6) используется для определения положения упругого элемента подвески в любой момент времени, а также может быть применено для построения кинематической характеристики подвески в целом с использованием метода припасовки, заключающимся в следующем. Зная значение выбранного параметра, соответствующего положению статического равновесия подвески 
, определяют коэффициенты влияния и . Затем, задаваясь малым перемещением колеса ±
, по выражению (5) определяют соответствующее изменение угла ±, а по выражению (6) — изменение хода упругого элемента. В последствии алгоритм повторяется для угла =±.
Методику аналитического расчета кинематической характеристики подвески поясним на конкретном примере независимой двухрычажной подвески с неравными рычагами, кинематическая схема которой изображена на Рис.1.
Вначале получим уравнения связи вида (1) и (2).
Общую длину упругого элемента 
в любой момент времени можно определить из соотношения:
, (7)
где 
,
,
,
- координаты точек С и D соответственно в системе координат XOY.
Координаты точки D постоянны и равны:
, (8)
. (9)
Координаты точки С найдем, как точку пересечения двух окружностей с центрами Е, В и радиусами 
, 
соответственно.
Запишем систему уравнений:
|
|
|
, (10) |
где 
,
,
,
- координаты точек B и E.
Решая систему (10), получим: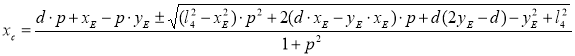
(11)
, (12)
где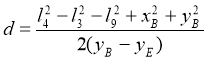 
, (13)
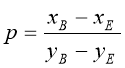. (14)
В выражении (11) знак перед корнем выбирают исходя из физического смысла. В данном случае знак выбирается тот, при котором ордината точки С имеет большее значение.
В выражения (11), (12), (13), (14) входят координаты точек Е и В. Координаты точки Е постоянны и равны:
, (15)
. (16)
Координаты точки В получим аналогично координатам точки С — в месте пересечения окружностей с центрами в точках А и Е и радиусами 
и 
соответственно.
|
|
|
, (17) |
Решение системы (17) дает:
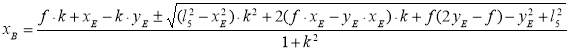(18)
, (19)
где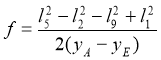 
, (20)
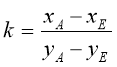. (21)
Знак перед корнем в выражении (18) определяют по аналогии с предыдущим случаем.
Координаты точки А в выражениях (20) и (21) находят по зависимостям:
, (22)
. (23)
Теперь все составляющие уравнения (7) определены, а, следовательно, получено первое уравнение связи, соответствующее выражению (1).
Получим второе уравнение связи, соответствующее выражению (2). Ординату точки М — центра колеса найдем из соотношения:
, (24)
где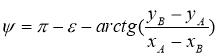 
. (25)
Выражение (24) является вторым уравнением связи.
Получим зависимости для коэффициентов влияния и .
Возьмем частную производную по углу 
от выражения (7):
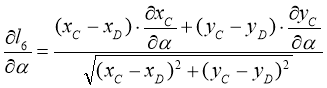. (26)
Частные производные 
и 
определяются по выражениям:
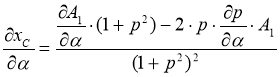, (27)
где
(28)
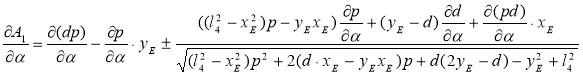(29)
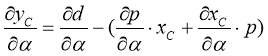. (30)
В выражения (27), (29), (30) входят частные производные 
, 
, 
, выражения для которых имеют вид:
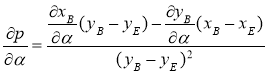, (31)
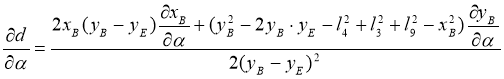, (32)
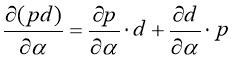. (33)
Возьмем частные производные 
и 
:
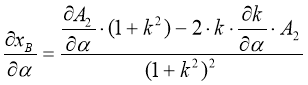, (34)
где
,(35)
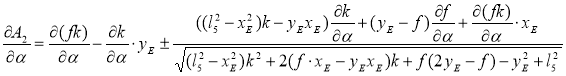, (36)
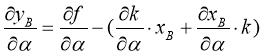. (37)
Выражения для частных производных, входящих в уравнения (34), (36), (37) имеют вид:
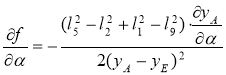, (38)
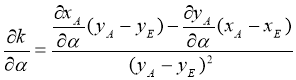, (39)
. (40)
В выражения (38), (39), (40) входят частные производные 
и 
, возьмем их:
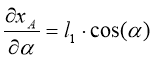, (41)
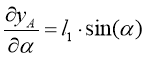. (42)
По выражениям (26)…(42) вычисляется коэффициент влияния 
.
Выражение для коэффициента влияния 
получим, взяв частную производную по 
от зависимости (24):
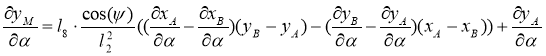. (43)
Окончательно, изменение длины упругого элемента подвески при изменении хода колеса на , найдем из соотношения вида (6):
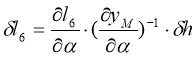. (44)
Несмотря на кажущуюся громоздкость полученных зависимостей, с использованием для расчета ЭВМ процесс получения кинематической характеристики подвески по приведенной методике значительно упрощается по сравнению с графическим и, кроме того, появляется возможность использования полученных выше выражений в более точных математических моделях транспортных средств, как колебательных систем.
В приложении 1 приведена программа расчета кинематической характеристики подвески на языке «Бейсик», а в таблице 1 результаты расчета для подвески МАЗ-547, изображенной на рис. 1.
Таблица 1
Результаты расчета кинематической характеристики подвески
|
h, м |
- 0,14 |
- 0,12 |
- 0,1 |
- 0,08 |
- 0,06 |
- 0,04 |
- 0,02 |
0 |
0,02 |
|
lp, м |
- 0,091 |
- 0,077 |
- 0,063 |
- 0,05 |
- 0,037 |
- 0,025 |
- 0,012 |
0 |
0,012 |
|
h, м |
0,04 |
0,06 |
0,08 |
0,1 |
0,12 |
0,14 |
0,16 |
0,18 |
0,2 |
|
lp, м |
0,024 |
0,036 |
0,048 |
0,059 |
0,07 |
0,08 |
0,091 |
0,1 |
0,11 |
Исходные данные для расчета:
м; 
м; 
м; 
м; 
м;
м; 
м; 
м; 
м; 
;
; 
; 
.
Приложение 1
Программа расчета кинематической характеристики
5 DIM Y(2) , X(2) , M(2) , O(2) , T(2) , C(2) , U(2) , V(2)
10 INPUT “l1,l2,l3,l4,l5,l6,l7,l8,l9,l0,b,g,e,ar (Длины в метрах, углы в град)”;
L1,L2,L3,L4,L5,L6,L7,L8,L9L0,B,G,E,AR
15 CLS
16 ? TAB(10) “Расчет кинематической характеристики подвески”
17 ? “ “
20 XD=L0*SIN (G*P1/180)
30 YD=L0*COS(G*P1/180)
40 XE=L9*SIN(B*P1/180)
50 YE=L9*COS(B*P1/180)
60 FOR I=1 TO 2
70 A=AR*P1/180
80 H=0
90 FF!=0 !
100 FOR J=1 TO 10
110 IF I=1 THEN N=1 ELSE N=(-1)
120 H=H+0.02*N
130 XA=L1*SIN (A)
140 YA=(-L1)*COS(A)
150 AX=L1*COS(A)
160 AY=L1*SIN (A)
170 DK= (AX*(YA-YE)-AY*(XA-XE)) / (ABS(YA-YE)^2)
180 DF= (( L9^2 +L2^2-L5^2-L1^2)*AY) / (2*ABS (YA-YE)^2)
190 K=(XA-XE)/(YA-YE)
200 F=(L5^2-L2^2+L1^2-L9^2) / (2*(YA-YE))
210 FK=DF*K+DK*F
220 FOR Q=1 TO 2
230 IF Q=1 THEN W=1 ELSE W= (-1)
240 O(Q)=SQR ((L5^2-XE^2)*ABS(K)^2+2*(XE*F-XE*YE)*K+F*
(2*YE-F)-YE^2+L5^2)*W
250 M(Q)= F*K+XE-K*YE+O(Q)
260 X(Q)=M(Q)/(1+ABS(K)^2)
270 Y(Q)=F-K*X(Q)
280 NEXT Q
290 IF Y(1)>Y(2) THEN GOTO 350
300 YB=Y(2)
310 XB=X(2)
320 M=M(2)
330 O=O(2)
340 GOTO 390
350 YB=Y(1)
360 XB=X(1)
370 M=M(1)
380 O=O(1)
390 DM=FK-DK*YE+(((L5^2-XE^2)*K-XE*YE)*DK+(YE-F)*DF+FK*XE)/O
400 BX= (DM*(1+ABS(K)^2)-2*K*DK*M)/((1+ABS(K)^2)^2)
410 BY=DF-(DK*XB+BX*K)
420 D= (L4^2-L3^2-L9^2+ABS(XB)^2+ABS(YB)^2)/(2*(YB-YE))
430 P= (XB-XE)/(YB-YE)
440 DP=(BX*(YB-YE)-BY*(XB-XE))/(ABS(YB-YE)^2)
450 DD=(2*XB*(YB-YE)*BX+(ABS(YB)^-2*YB*
YE-L4^2+L3^2+L9^2-ABS (XB)^2)*BY)/(2*ABC(YB-YE)^2)
460 PD=DP*D+DD*P
470 FOR R=1 TO 2
480 IF R=1 THEN Z=1 ELSE Z=(-1)
490 U(R)= SQR ((L4^2-XE^2)*ABS(P)^2+2*(D*XE-YE*XE)*P+D*
(2*YE-D)-YE^2+L4^2)*Z
500 V(R)= D*P+XE-P*YE+U(R)
510 C(R)=V(R)/(1+ABS(P)^2)
520 T(R)= D-P*C(R)
530 NEXT R
540 IF T(1)>T(2) THEN GOTO 600
550 YC=T(2)
560 XC=C(2)
570 U=U(2)
580 V=V(1)
590 GOTO 640
600 YC=T(1)
610 XC=C(1)
620 U=U(1)
630 V=V(1)
640 DV=PD-DP*YE+(((L4^2-XE^2)*DP+(YE-D)*DD+PD*XE)/ U
650 CX=(DV*(1+ABS(P)^2)-2*P*DP*V)/((1+ABS(P)^2)^2)
660 CY=DD-(DP*XC+CX*P)
670 DL=ABS(((XC-XD)*CX+(YC-YD)*CY)/(SQR(ABS(XC-XD)^2+ABS(YC-YD)^2)))
680 KS=P1-E*P1/180-ATN((YB-YA)/(XA-XB))
690 MY= ABS((L8*COS(KS)/(L2^2))*((AX-BX)*(YB-YA)-(BY-AY)*(XA-XB))+AY)
700 AD=0.02*N/MY
710 LF!=DL*AD
720 FF!=FF!+LF!
730 ? TAB(15) “h=”; H; “ “ ; “f=”; FF!
740 A=A+AD
750 NEXT J
760 NEXT I
770 END
Литература:
- Антонов А. С., Кононович Ю. А. и др. Армейские автомобили. Теория.- М.: Военное издательство МО СССР, 1970, 526 с.
- Степанченко Э. П., Фалалеев П. П. Технологическое оборудование.- М.: МО СССР, 1986, 364 с.
- Литвинов А. С., Фаробин Я. Е. Автомобиль: Теория эксплуатационных свойств: Учебник для вузов по специальности «Автомобили и автомобильное хозяйство». — М.: Машиностроение, 1989.—240 с.
- Вахламов В. К. Автомобили: Эксплуатационные свойства: учебник для студ. Высш. Учеб. Заведений — М.: Издательский центр «Академия», 2006.-240 с.
