В работе описано численное моделирование течения двухфазного потока в водовоздушном эжекторе для модели турбулентности k-ε. Результаты моделирования представлены в виде линий токов пассивного и активного потоков и распределения давления внутри эжектора.
Ключевые слова: эжектор, аэрация, ANSYS CFX.
Водовоздушный эжектор относится к классу струйных аппаратов и предназначен для получения водовоздушной смеси при взаимодействии рабочей жидкости с воздухом [1].
Аэрирование воды при помощи эжекторных устройств получило широкое распространение благодаря простоте их конструкции, высокой надежности, экономичности применения. В проточной части этого устройства происходит смешение струй, находящихся в разных фазовых состояниях, с образованием смеси. При этом активным рабочим телом является жидкость, а пассивным — газ. Таким образом, аэрирование эжекторами основано на использовании энергии рабочей жидкости, движущейся линейно со скоростью 15–17 м/с через сопло, имеющее определенные форму и размеры, для получения перепада давления, создающего эжекцию газовой или жидкой фазы.
Для проведения численного моделирования работы водовоздушного эжектора в структурной схеме модуля Fluid Flow (CFX) была создана геометрическая модель проточной части эжектора (рис. 1).
На основе геометрической модели, подготовленной в блоке Geometry, создается сеточная, или конечно-элементная модель [2].
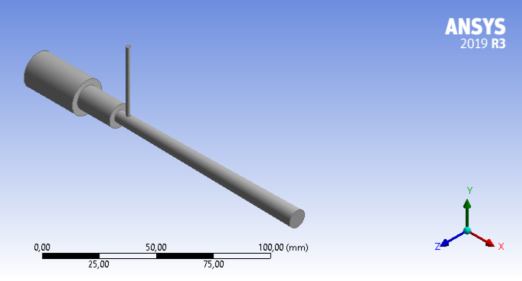
Рис. 1. Трехмерная модель водовоздушного эжектора
Для исследуемого водовоздушного эжектора была построена неструктурированная сетка (рис. 2 и 3) с количеством элементов (ячеек) равным 59853.
Результаты численного моделирования (сходимость расчета, точность моделирования физических процессов, погрешность расчета, время вычисления) во многом зависят от расчетной сетки. При этом необходимое качество конечно-элементной сетки является основополагающим критерием для успешного численного расчета.

Рис. 2. Неструктурированная сетка геометрической модели
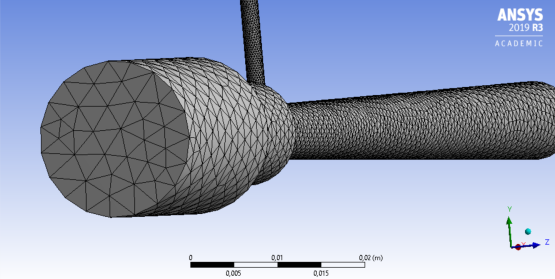
Рис. 3. Ячейки неструктурированной сетки геометрической модели
Для численного моделирования двухфазного течения в эжекторе необходимы граничные условия, которые задаются в блоке Setup.
В расчетной области в качестве физической природы домена был выбран тип Fluid Domain — текучий домен используется для моделирования жидких и газообразных тел [2]. В качестве модели течения была выбрана k-Epsilon модель.
Для определения поведения среды на внешней границе рассматриваемой области задавались следующие граничные условия (рис. 4):
- water (тип граничного условия Inlet) — вход активного потока (воды).
- air (тип граничного условия Inlet) — вход пассивного потока (воздуха).
- wall (тип граничного условия Wall) — непроницаемая граница для потока среды.
- out (тип граничного условия opening) — выход водовоздушной смеси из диффузора эжектора.

Рис. 4. Расчетная модель водовоздушного эжектора
Анализ литературы [3, 4, 5] показал, что наиболее подходящей для подобного типа задач является k-ε модель турбулентности. В вычислениях принята модель с параметрами k = 0,05 и ε = 10 — для граничных условий water и air и k = 0,01и ε = 1 — для выходного сечения out.
На рис. 5 и 6 представлены результаты численного моделирования двухфазного течения в водовоздушном эжекторе.

Рис. 5. Траектории линий токов активного (воды) и пассивного (воздух) потоков в водовоздушном эжекторе

Рис. 6. Распределение давлений в водовоздушном эжекторе
Выводы: проведено численное моделирование течения двухфазного потока в водовоздушном эжекторе. Однако без достоверных результатов физических экспериментов и их сопоставления с результатами моделирования невозможно говорить об адекватности разработанных моделей. Поэтому дальнейшим шагом в изучении процесса смешения активного и пассивного потоков в водовоздушном эжекторе является проведение экспериментального исследования и верификация полученных данных с результатами численного моделирования. В случае совпадения контуров скорости, полученных в численном и вычислительном эксперименте, можно утверждать, что выбранные настройки решателя и константы модели турбулентности максимально точно описывают физический процесс.
Литература:
- Лямаев Б. Ф. Гидроструйные насосы и установки. Л.: Машиностроение. Ленингр. отд-ние, 1988. 256 с.: ил.
- Шарай Е. Ю. Компьютерное моделирование многофазных течений при решении задач техносферной безопасности: учеб. пособие / Е. Ю. Шарай; под ред. В. А. Девисилова. — М.: ИНФРА-М, 2019. — 128 с.
- Long X., Han N. and Chen Q. Influence of nozzle exit tip thickness on the performance and flow field of jet pump // Journal of Mechanical Science and Technology. — 2008. — 22. — pp. 1959–1965.
- Xiao L. Z. [et al.] Numerical investigation on the cavitating flow in annular jet pump under different flow rate ratio // 27th IAHR Symposium on Hydraulic Machinery and Systems. — 2014.
- Xiao L. Z. and Long X. L. Cavitating flow in annular jet pumps // International Journal of Multiphase Flow. — 2015. — 71. — pp. 116–132.

