В данной работе описываются способы определения коэффициентов активности изотермической системы ацетон — пропанол с помощью полуэмпирических методов расчёта и с помощью модели UNIFAC.

Физико-химические свойства системы

Таблица 1

Основные физико-химические параметры компонентов системы

Ацетон — бесцветная подвижная летучая жидкость с характерным резким запахом. Во всех соотношениях смешивается с водой, диэтиловым эфиром, бензолом, метанолом, этанолом, многими сложными эфирами. Органическое вещество, имеющее формулу CH3–C(O)–CH3, простейший представитель насыщенных кетонов.

Пропанол — одноатомный спирт. Встречается в природе в небольших количествах как продукт ферментации. Бесцветная жидкость со спиртовым запахом, смешивается с водой и образует с ней азеотропную смесь. Растворим в этаноле, диэтиловом эфире, ацетоне, бензоле и других органических растворителях.

Исходные данные:

1) Бинарная система (ацетон — пропанол)

2) Паровая фаза считается идеальной (подчиняется закону Дальтона)

3) Давления насыщенных паров компонентов системы рассчитаны по уравнению Антуана

4) Коэффициенты активности компонентов системы рассчитаны по методу UNIFAC

5) Система изотермическая (25 ⁰С)

Подставив исходные данные в программу ChemSep, были получены данные о равновесии в системе:

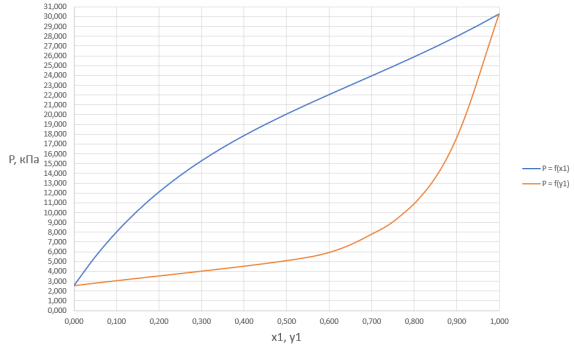
Рис. 1. График зависимости общего давления в системе от содержания ацетона в жидкой и газовой фазах

Таблица 2

Составы равновесных фаз для системы ацетон (1) –пропанол (2) при общем давлении Ри температуре 25º C

Таблица 3

В связи с низким общим давлением в системе при заданной температуре и отсутствием сильной ассоциации компонентов в паровой фазе считаем данную паровую систему идеальной. При этом допущении расчет коэффициентов активности компонентов возможен по уравнению:

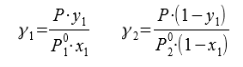
Где х₁, у₁ — доли ацетона в жидкой и паровой фазах соответственно

Р — общее давление в системе

,− давление чистых ацетона и пропанола соответственно

Построив график зависимости ln(γ₁/γ₂) = f(x₁) можем сделать вывод о термодинамической согласованности данных.

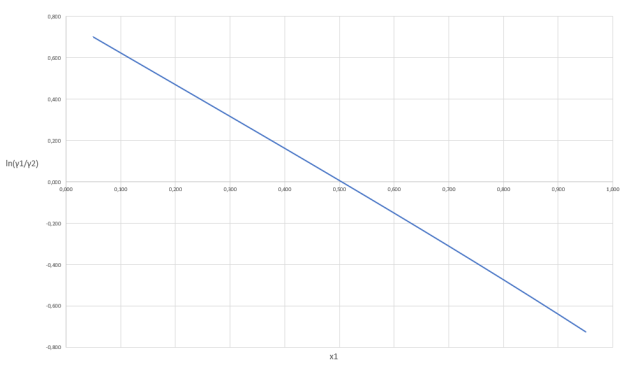
Рис. 2. График зависимости логарифма отношения коэффициентов активности от содержания ацетона в жидкой фазе

Так как площадь под графиком равна 0, то система является термодинамически согласованной.

Полуэмпирические модели

В случае полуэмпирических моделей структура модельных уравнений выводится из теории растворов, но обработка экспериментальных данных совершается с использованием регрессионных параметров.

Модель Вильсона

Наибольшее распространение обрела модель «локальных составов». Первое уравнение, образованное на этой модели, было выведено в 1964 г. Вильсоном. Модель «локальных составов» основана на том, что в результате межмолекулярных взаимодействий в смеси начинаются локальные микросоставы, неэквивалентные макросоставу раствора по приготовлению. Разница локальных и средних концентраций компонентов связанна с разностью энергией взаимодействия одноименных и разноименных пар молекул.

Для расчета коэффициентов активности компонентов бинарной системы применяются следующие уравнения:

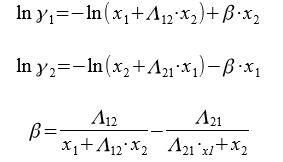
Где Λ₁₂, Λ₂₁ — приведенные параметры, оцениваемые по экспериментальным данным для данной системы.

Между параметрами уравнения Вильсона и коэффициентами активности компонентов при бесконечном разбавлении получаются следующие зависимости:

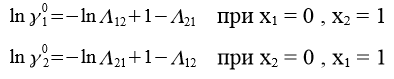
С помощью номограммы определяем начальные значения Λ₁₂ = 0,7, Λ₂₁ = 0,6 при = 2,16, = 2,28 и рассчитываем уточненные значения приведенных параметров.

В итоге получаем вытекающие значения приведенных параметров: Λ₁₂ = 0,693, Λ₂₁ = 0,596. Далее ищем значения β и затем ɣ₁, ɣ₂.

Главный минус модели Вильсона заключается в том, что уравнение, как правило хорошо описывающее равновесие жидкость — пар, непригодно для представления данных о равновесии жидкость — жидкость.

Значительное преимущество уравнения Вильсона в сравнении с эмпирическими уравнениями — способность описания поведения многокомпонентных смесей, если известны приведенные параметры для всех составляющих бинарных систем.

Предложены различные модификации уравнения Вильсона, разрешающие ликвидировать его главный недостаток — плохое описание поведения гетерогенных систем.

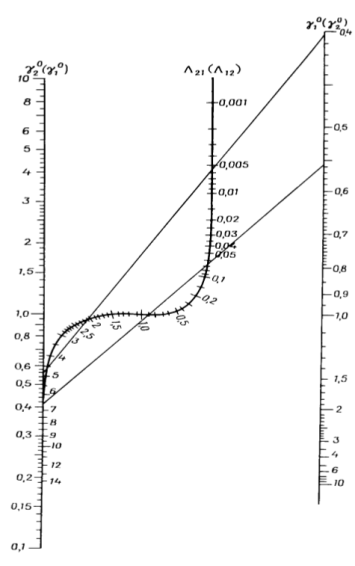
Рис. 3. Номограмма для определения приведенных параметров уравнения Вильсона

Модель NRTL

Одна из модификаций была выведена Реноном и Прауснитцем в 1968 г. уравнение NRTL (nonrandom two-liquid). Оно также основано на концепции локальных составов и на теории, согласно которой жидкость имеет ячеистую структуру.

Для бинарной системы:

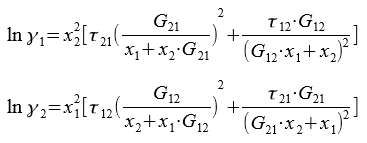
Приведённые энергетические параметры τ₁₂ и τ₂₁ находим, решив систему уравнений:

Далее находим переменные G₁₂ и G₂₁, характеризующие энергию взаимодействия:

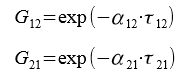
α₁₂ = 0,5 — параметр, характеризующий степень упорядоченности распределения молекул в растворе

Решая системы уравнений, находим значение переменных τ₁₂ = 0,515 и τ₂₁ = 0,372. Далее находим G₁₂ = 0,773 и G₂₁ = 0,83.

Математическая форма уравнений обеспечивает модели NRTL большую гибкость, способность описывать самые различные типы зависимости коэффициентов активности от состава. Сохраняя основные достоинства уравнений Вильсона, уравнения NRTL способны также описывать системы с расслаиванием, благодаря чему их часто используют для расчета равновесий жидкость — жидкость и жидкость — жидкость — пар.

Теоретические модели. Метод UNIFAC

Теоретические модели позволяют рассчитывать коэффициенты активности на основании свойств чистых компонентов.

Метод UNIFAC (universal functional activity coefficient — универсальный функциональный коэффициент активности) был разработан в 1975 году Фреденслундом, Джонсом и Праузницем. Данный метод рассчитывает величины коэффициентов активности на основе концепции группового вклада. Предполагается, что взаимодействия между двумя молекулами являются функцией взаимодействий между группами. Для расчета коэффициентов активности этим групповым методом применяется вариант модели локальных составов UNIQUAC. Уравнение UNIQUAC (UNIversal QUAsi-Chemical equation), совмещает в себе концепцию локального состава с квазихимической решеточной теорией Гуггенгейма — Ставермана. Величины коэффициентов активности γ_i рассматривают как сумму двух вкладов — комбинаторного, обусловленного различиями в размерах и форме молекул, и остаточного, определяемого в основном энергетикой межмолекулярных взаимодействий.

Для расчета коэффициентов активности компонентов бинарной системы при заданной температуре и составе системы молекулы компонентов разбиваются на подгруппы.

Таблица 4

Геометрические параметры модели UNIFAC

Таблица 5

Параметры взаимодействия групп

При помощи программного обеспечения Mathcad нами были рассчитаны комбинаторные и остаточные части коэффициентов активности компонентов. Далее суммированием этих составляющих мы нашли коэффициенты активности каждого компонента.

По информативности и точности метод UNIFAC, как правило, ненамного уступает строгим методам, но существенно превосходит их с точки зрения экономии вычислительных затрат, что позволяет не проводить массовые расчеты.

Литература:

1. Гайле А. А., Сомов В. Е., Процессы разделения и очистки продуктов переработки нейти и газа: Учеб.пособие. — Спб.: ХИМИЗДАТ, 2012. — 376 с.
2. Несмеянов А. Н., Несмеянов Н. А., Начала органической химии. т.1- М.: Химия, 1969. — 664 с.
3. Справочник химика. Том 1. Общие сведения, строение вещества, свойства важнейших веществ, лабораторная техника. / Под ред. Б. П. Никольского — М.-Л.: Химия, 1966–1071 с.