Приступая к учебе в высшем техническом учебном заведении, первокурсник сталкивается с множеством проблем, одна из которых − проблема адаптации к учебному процессу вуза.
Проблема адаптации тесно связана с формами учебных занятий: лекционными, практическими, лабораторными, семинарскими, дополнительными и т.д. В связи с чем, особенно важными являются систематическая работа студентов и проверка качества, полученных ими при этом знаний.
Высшая математика является базовой дисциплиной в высшем техническом учебном заведении и играет большую роль в учебном процессе. Контроль знаний и умений студентов является одним из элементов учебного процесса. В процессе обучения контролю знаний и умений студентов отводится проверочная, обучающая, развивающая, воспитательная и методическая функции. Для осуществления этих функций предлагается организовать обучение математике следующим образом. Материал курса математики, изучаемый в семестре, можно разделить на три-четыре блока. Оценка работы студентов, их знаний и умений проводится во всех блоках и для всех форм учебных занятий: лекционных, практических, дополнительных.
Каждый блок включает в себя выполнение типового расчета, самостоятельных работ, контрольных работ, домашних заданий и промежуточных зачетов по соответствующим темам.
На практических занятиях студентам предлагается раздаточный материал: основные формулы по изучаемой теме (или краткий конспект лекций), так называемые «таблицы»[1]. «Таблицы» позволяют быстрее проводить этап актуализации знаний, более того происходит экономия места на доске. Изучив «таблицы», студенты могут увидеть, что им предстоит изучить сегодня, на следующем занятии, вспомнить материал предыдущего занятия. Целесообразно использовать «таблицы» на дополнительных занятиях с отстающими студентами: по «таблицам» легко разобрать материал лекций и приступить к решению практических задач.
Для проверки качества, полученных студентами знаний, предлагается ввести уровневую дифференциацию учебного материала курса высшей математики.
В методике преподавания математики ранжирование задач по уровням проводится различными методами. Традиционно выделяют четыре уровня усвоения знаний, с каждым из которых связано решение определенных задач: первый ─ уровень знакомства (решение задач на уровне памяти), второй ─ уровень репродуктивности (решение задач, требующих воспроизведение теории на уровне понимания), третий ─ уровень умений и навыков (решение задач, позволяющих проверить умение применять теорию), четвертый ─ уровень трансформации (решение нестандартных задач на уровне проблемного применения теории).
Основываясь на вышеперечисленных уровнях можно разработать самостоятельные и контрольные работы, состоящие из четырех уровней. При этом I уровень оценивается альтернативной оценкой «зачтено» ─ «не зачтено», I + II уровни ─ оценкой «3», I + II + III ─ оценкой «4», I + II + III + IV ─ оценкой «5». Каждый студент имеет право добровольно и сознательно решать для себя, на каком уровне ему усваивать материал (I и II уровни минимально обязательные для каждого студента). Задания первого и второго уровня – это базовые знания, которыми должен обладать каждый студент. На их основе происходит овладение материалом на более высоком уровне.
Приведем пример самостоятельной работы по теме «Плоскость».
|
Вариант-1 | |
|
I |
Вычислить угол между плоскостями |
|
II |
Написать уравнение плоскости, проходящей через точку |
|
III |
Написать уравнение плоскости, проходящей через начало координат и перпендикулярной к плоскостям: |
|
IV |
Плоскость, в которой лежит ось |
Аналогичные требования предъявляются к промежуточному зачету и к экзамену по
высшей математике.
Например, экзаменационный билет № 1 (1 семестр).
|
МПС ОмГУПС Кафедра «Высшая математика» |
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №__1__
По дисциплине «Высшая математика» |
УТВЕРЖДАЮ: Зав. кафедрой | |
|
2008 /2009 уч.год | |||
|
1. |
Скалярное произведение. Свойства скалярного произведения. | ||
|
2. |
Задание плоскости в пространстве точкой и двумя векторами. | ||
|
3. |
I. Запишите правило треугольника вычисления определителя третьего порядка. | ||
|
|
II. Когда три вектора а, в, с компланарны? | ||
|
|
III. Решить систему линейных алгебраических уравнений, используя формулы Крамера: | ||
|
|
IV. Зеркальная поверхность прожектора образована вращением параболы вокруг ее оси симметрии. Диаметр зеркала 80 см, а глубина его 10 см. На каком расстоянии от вершины параболы нужно поместить источник света, если для отражения лучей параллельным пучком он должен быть в фокусе параболы? | ||
При этом студентам известно, чтобы получить оценку «удовлетворительно» необходимо сформулировать определения, оценку «хорошо» ─ дать полный ответ ( сформулировать определения, перечислить все свойства,…), оценку «отлично» ─ помимо полного ответа, необходимо доказать свойство.
Таким образом, студенту предлагается четыре задачи разного уровня сложности. Тех же целей можно достичь, предложив студенту одну задачу: общее условие и несколько заданий разного уровня сложности. Такую самостоятельную работу характеризует единство тематики. Приведем в качестве примера вариант самостоятельной работы по теме «Скалярное, векторное и смешанное произведение».
|
Вариант-1 | |
|
Даны четыре точки: | |
|
1) |
координаты векторов |
|
2) |
углы |
|
3) |
площади всех граней; |
|
4) |
объем пирамиды; |
|
5) |
все четыре высоты пирамиды. |
При этом, чтобы получить оценку «удовлетворительно», необходимо выполнить первое и второе задания, оценку «хорошо» ─ первое, второе и третье задания, оценку «отлично» ─ первое, второе, третье и четвертое задания. Пятое задание является дополнительным для студента претендующего на оценку «отлично».
Введение подобной дифференциации избавляет от вопросов студентов: «Сколько нужно решить, чтобы получить 4?» и т.д. Студент может самостоятельно оценить свои возможности и выбрать для себя тот уровень целей, который соответствует его возможностям и потребностям в данный момент времени. Это позволит студенту при возможности и возникшем интересе перейти на более высокие уровни на любом этапе обучения.
В течение семестра осуществляется контроль посещаемости студентами лекционных, практических и дополнительных занятий. Подведение итогов работы студентов в каждом блоке проводится на контрольной неделе. Такой контроль дисциплинирует студента, воспитывает у него чувство ответственности за свою работу, стимулирует серьезное и добросовестное отношение к активной учебной деятельности.
В конце первого семестра студентами самостоятельно проводится обзорная лекция. Несколько студентов выступают с рефератами об ученых математиках, чьи теоремы и правила изучались в прошедшем семестре. Доклад состоит из двух частей: в первой части студент рассказывает о жизни математика и о его открытиях, во второй части студент говорит непосредственно о том, что изучалось в семестре.
Таким образом, за одну лекцию повторяется практически весь материал семестра. Более того, студенты учатся планировать свое выступление, выступать с докладами, удерживать внимание аудитории. Все это вместе способствует развивающей, обучающей и воспитательной функциям.
В следующих семестрах лучшие студенты выступают с докладами о проведенных исследованиях. Обычно это решение какой-либо задачи с применением теорем и формул, изученных в текущем семестре. Как правило, решение такой задачи носит пропедевтический характер: с ней студенты будут иметь дело в следующих семестрах. Например, доклад на тему «Исследовать функцию 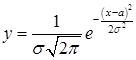 и построить ее график». С этой функцией студенты столкнутся при изучении нормального распределения.
и построить ее график». С этой функцией студенты столкнутся при изучении нормального распределения.
В конце семестра подводятся общие итоги успеваемости студентов. Каждому студенту выставляется оценка за работу в семестре. Если в конце семестра предусмотрен зачет, то он выставляется автоматически при выполнении всех самостоятельных и контрольных работ на положительные оценки. Если в конце семестра предусмотрен экзамен, то он выставляется автоматически (среднее арифметическое всех оценок за контрольные работы и промежуточные зачеты). Студенты, претендующие на более высокую оценку, могут пересдать промежуточный зачет и переписать контрольную работу по соответствующей теме. Студентам, выступавшим на обзорной лекции, оценка на экзамене повышается на один балл. Студенты, получившие оценку «неудовлетворительно» за работу в семестре, сдают экзамен на общих основаниях.
Такой подход видится оптимальным в современных условиях снижения уровня базовой подготовки первокурсников[2]. Такой подход дисциплинирует студентов, приучает их к планомерному и продуктивному труду, что в свою очередь приводит к повышению качества полученных ими при этом знаний.
Литература
- Болотюк В.А., Болотюк Л.А. Высшая математика. – Омск: Изд-во ОмГПУ, 2008. 84с.
- Байдак В. А. Теория и методика обучения математике: наука, учебная дисциплина: монография. – Омск: Изд-во ОмГПУ, 2008. 264с.
- Каплан Б.С., Рузин Н.К., Столяр А.А. Методы обучения математике. – М.: Просвещение, 1981. 192с.
- Кирсанов А.А. Индивидуализация учебной деятельности как педагогическая проблема. – Казань: Изд-во Казанского университета, 1998. 224с.
- Конаржевский Ю.А. Система. Урок. Анализ. – Псков: ПОИПКРО, 1996. 440с.
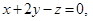
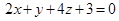 .
.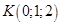 и содержащей ось
и содержащей ось 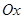 .
. 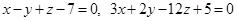 .
.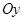 , составляет с плоскостью
, составляет с плоскостью 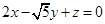 угол
угол 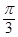 . Найти ее уравнение.
. Найти ее уравнение.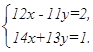
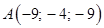 ,
, 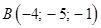 ,
, 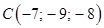 ,
,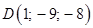 . Найти:
. Найти: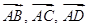 и длины всех ребер пирамиды
и длины всех ребер пирамиды 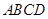 ;
;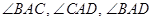 ;
;
