В статье рассматривается использование кодов БЧХ для генерации набора кодовых слов заданной длины N, отстоящих друг от друга на расстояние Хэмминга d.
Код БЧХ (n; k, t) задается набором параметров: n — длина кодового слова, k — число информационных бит, причем n=2m– 1, где m– челое число, t — число исправляемых ошибок кода. Параметр t определяет значение и порядок порождающего полинома кода
g(x) = xn-k-1 + cn-k-2xn-k-2 + … + c1x +c0,
сi — коэффициенты, принимают значения 0 или 1.
Параметр t определяет также дистанционные свойства кода, минимальное расстояние Хемминга между кодовыми словами d= 2t+1.
Алгоритм расчета порождающего полинома кода по заданным n, m и t рассмотрен в [1].
Для практических расчетов порождающего полинома можно использовать средства пакета Matlab:
dim=4; % %размерность поля кода
t=1; % %число исправляемых ошибок
m = gfprimdf(dim); cs = gfcosets(dim); pl = gfminpol(cs(2: t+ 1, 1), m);
FACTORS = pl;
GENPOLY = gftrunc(pl(1,:)); % %генераторный (порождающий) полином,
fori = 2: t
GENPOLY = gfconv(GENPOLY, gftrunc(pl(i,:)));
end;
r=size(GENPOLY,2); % %число степеней полинома, включая нулевую.
В таблице 1 приведены генераторные полиномы для кодов БЧХ с длиной кодового слова 15 и 31. Для четных d надо полином с меньшим d умножить на (х+1). В таблице 1 для примера приведен один такой полином (n=15, d=4).
Таблица 1
Параметры кодов БЧХ
|
Размерность поля (dim) |
Число исправляемых ошибок(t)/ расстояние Хемминга d |
Степень полинома (r) |
Код БЧХ |
GENPOLY 1+х + … + хr-1 |
|
4(15) |
1/ 3 |
5 |
(15,10) |
1100 1 |
|
-/ 4 |
6 |
1101 01 |
||
|
2/ 5 |
9 |
(15,6) |
1000 1011 1 |
|
|
3/ 7 |
11 |
(15,4) |
1110 1100 101 |
|
|
5(31) |
1/ 3 |
6 |
(31,25) |
1010 01 |
|
2/ 5 |
11 |
(31,20) |
1001 0110 111 |
|
|
3/ 7 |
16 |
(31,15) |
1111 0101 1111 0001 |
|
|
4/ 9 |
21 |
(31,10) |
1010 1011 0110 0100 0110 1 |
|
|
5/ 11 |
26 |
(31,5) |
1110 0100 0101 0111 1011 0100 11 |
Используя свойство кода БЧХ — расстояние Хемминга между двумя кодовыми словами не менее d= 2t+1, можно генерировать слова кодовые слова длиной Nс расстоянием Хемминга d. Для кода (n, k) значение N будет лежать в диапазоне от (k+1) до n. При этом число кодовых слов с расстоянием Хэмминга d равно 2N-k.
Для генерации кодовых слов необходимо построить порождающую матрицу, первая строка которой формируется по порождающему полиному. Например, для кода БЧХ(15, 10) порождающий полином равен g= х4 + х +1 (таблица 1), биты с 0 по 4 соответствуют коэффициентам полинома — 10011, а остальные биты (14–5) заполняются 0.
Каждая следующая строка матрицы получается сдвигом влево предыдущей строки, пока в старшем разряде не будет 1. Число строк порождающей матрицы равно (k+1).
В таблице 2 приведена порождающая матрица кода БЧХ(15, 10), число строк матрицы — 11.
Каждая строка i матрицы соответствует слагаемому xi (S0 — x0 (1), S1 — x1 (x), …, S10 — x10) полинома данных порядка k. Кодовые слова получаются побитовым XOR строк порождающей матрицы, соответствующих полиному исходных данных.
Таблица 2
Порождающая матрица кода БЧХ(15, 10)
|
Номер кодового слова |
Код слова (CC10) |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
S0 -1 |
19 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
S1- х |
38 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
S2– х2 |
76 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
S3– х3 |
152 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
S4– х4 |
304 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
S5– х4 |
608 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
S6– х6 |
1216 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
S7– х7 |
2432 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
S8– х8 |
4864 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
S9– х9 |
9728 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
S10–х10 |
19456 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Например, длина кодового слова N=8, для расчета слов используем строки S0 — S7. Слову с номером 11010010 соответствует полином х7 +х6 + х4 +х, оно равно S7 XOR S6 XOR S4 XORS1: 000110001010110.
В таблице 3 приведены 16 кодовых слов для N=8. Для генерации слов с N=7 из таблицы 2 нужно взять только 8 первых строк (без 7 бита).
Число кодовых слов кода БЧХ зависит от параметров кода n, k и t, которые определяют степень порождающего полинома r для заданного расстояния Хемминга d, длины кодового слова L.
На рисунке 1 приведена зависимость числа кодовых слов от расстояния Хемминга для кодов с разной длиной, по оси ординат приведен lgN (для L=511 данные приведены только для d в диапазоне от 3 до 48).
Из графиков рисунка 1 видно, что максимальное расстояние Хемминга кодовых слов, которое может быть получено с использованием кодов БЧХ равно примерно ¼ длины кодового слова, при этом с увеличением d число кодовых слов сильно уменьшается.
Один и тот же код БЧХ можно использовать для генерации кодовых слов разной длины, в таблице 4 показано число кодовых слов для кода БЧХ (31, k).
Таблица 3
Кодовые слова длиной 8, расстояние Хемминга 3
|
Полином |
Номер слова |
Биты кодового слова |
|||||||
|
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
||
|
0 |
0000 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0001 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
х |
0010 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
х+1 |
0011 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
х2 |
0100 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
х2+ 1 |
0101 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
х2+х |
0110 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
х2+х+1 |
0111 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
x3 |
1000 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
x3+1 |
1001 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
x3+х |
1010 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
x3+х+1 |
1011 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
x3+х2 |
1100 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
x3+х2+ 1 |
1101 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
x3+х2+х |
1110 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
|
x3+х2+х+1 |
1111 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
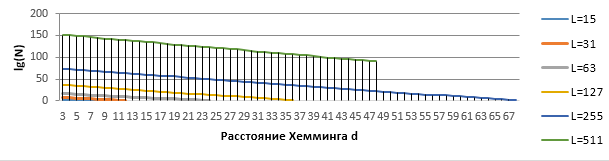
Рис. 1. Зависимость числа кодовых слов от расстояния Хемминга
Выводы: алгоритм с использованием кодов БЧХ позволяет эффективно рассчитывать кодовые слова с заданными значениями длины кодового слова и расстояния Хэмминга, при этом удовлетворение требований по расстоянию Хэмминга обеспечивается свойствами кода и не требует дополнительной проверки, что значительно снижает временные затраты. Число возможных кодовых слов при использовании кода БЧХ заранее известно, это число зависит: от парамертов кода БЧХ и от длины кодового слова. Наибольшее количество слов будет для кодовых слов с длиной (2m — 1), совпадающих с параметром n кода БЧХ, т. е. для 31, 63, 127, …, для других значений длин число слов с заданным растоянием Хемминга быстро убывает с уменьшением длины кодового слова.
Таблица 4
Число кодовых слов для кода БЧХ (31, k)
|
d |
Длина кодового слова N |
||||||||||||||
|
30 |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
16 |
|
|
3 |
16777216 |
8388608 |
4194304 |
2097152 |
1048576 |
524288 |
262144 |
131072 |
65536 |
32768 |
16384 |
8192 |
4096 |
2048 |
1024 |
|
4 |
8388608 |
4194304 |
2097152 |
1048576 |
524288 |
262144 |
131072 |
65536 |
32768 |
16384 |
8192 |
4096 |
2048 |
1024 |
512 |
|
5 |
524288 |
262144 |
131072 |
65536 |
32768 |
16384 |
8192 |
4096 |
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
|
6 |
262144 |
131072 |
65536 |
32768 |
16384 |
8192 |
4096 |
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
|
7 |
16384 |
8192 |
4096 |
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
8 |
8192 |
4096 |
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
|
9 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|||||
|
10 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
||||||
|
11 |
16 |
8 |
4 |
2 |
1 |
||||||||||
|
12 |
8 |
4 |
2 |
1 |
|||||||||||
Литература:
- Блейхут Р. Теория и практика кодов, контролирующих ошибки/ Блейхут Р. — М.: Книга по требованию, 2013. — 566 с.







