В данной статье рассмотрена система дифференциальных уравнений Лотки — Вольтерры, а также приведены формулировки доказательства первого и второго законов Вольтерры.

Ключевые слова: математика, дифференциальные уравнения, система Лотки — Вольтерры.

Существует множество практических приложений теории дифференциальных уравнений, одним из таковых является исследование конкуренции двух некоторых групп, называемых условно «хищниками» и «жертвами». Модель, описывающая данные взаимоотношения, была предложена в начале XX века Альфредом Лоткой и Вито Вольтеррой, работавшими независимо друг от друга.

Модель Лотки — Вольтерры представляет собой систему дифференциальных уравнений вида:

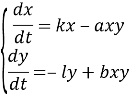
Где и — количество жертв и хищников соответственно,

— коэффициент рождаемости жертв, — коэффициент убыли хищников. При встречах хищников и жертв происходит убийство жертв с коэффициентом β, сытые хищники способны к воспроизводству с коэффициентом .

Для данной модели Вито Вольтерра вывел три закона [1], в данной статье мы рассмотрим и приведем доказательства для первого и второго закона Вольтерры. Все законы приведены в формулировке, представленной в учебном пособии «Модели динамики популяций» С. В. Соколова [2]δ

Первый закон Вольтерры сформулирован следующим образом: «Процесс уничтожения жертвы хищником нередко приводит к периодическим колебаниям численности популяций обоих видов, зависящим только от скорости роста популяций хищника и жертвы и от исходного соотношения их численности. Колебания численности двух видов периодическое, с периодом, зависящим как от начальной численности, так и от коэффициентов системы».

Докажем его, основываясь на методе В. И. Арнольда [3].

Теорема: Фазовые кривые системы замкнуты

Доказательство: Приведем данную систему к уравнению с разделяющимися переменными вида

Его интегральные кривые совпадают с фазовыми кривыми исходной системы в области, где x, y, bx-l и k-ay отличны от 0.

Следовательно,

Аналогично можем записать , где , и . Графики функций p и q имеют вид ям (рисунок 1 и 2), тогда и график функции p+q имеет такой же вид.

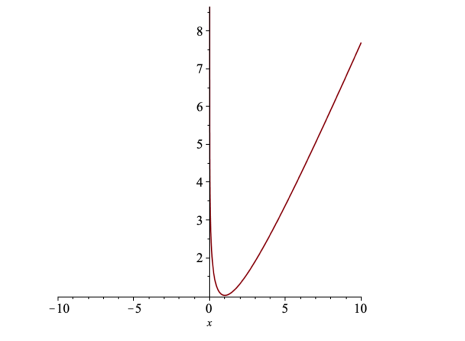
Рис. 1. Эскиз графика функции p(x)

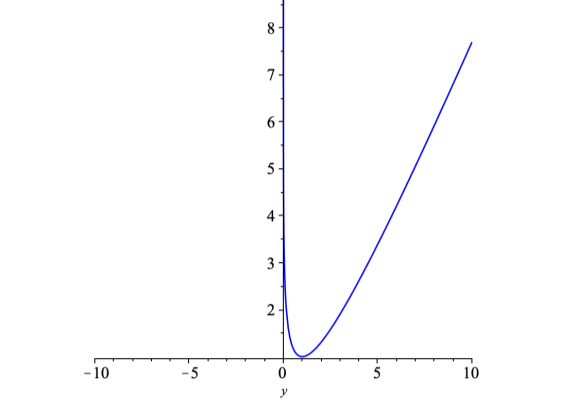
Рис. 2. Эскиз графика функции q(y)

Следовательно, линии уровня функции p+q являются замкнутыми кривыми (Рисунок 3), совпадающими с фазовыми кривыми исходной системы (Рисунок 4). Теорема доказана.

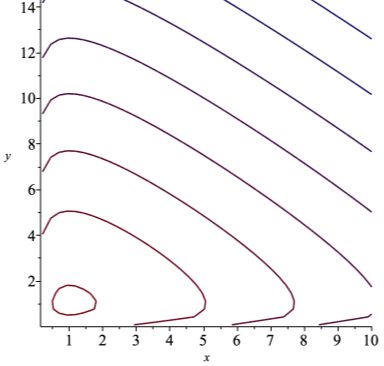
Рис. 3. Линии уровня функции p+q

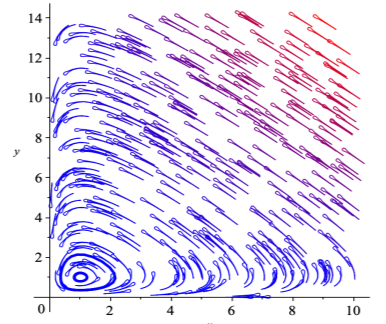
Рис. 4. Фазовые кривые системы Лотки-Вольтерра

Из замкнутости фазовых кривых следует, что x и y меняются со временем периодически. Первый закон Вольтерры доказан.

Второй закон Вольтерры: «Средняя численность популяции для каждого вида постоянна, независимо от начального уровня, при условии, что специфические скорости увеличения численности популяций, а также эффективность хищничества постоянны. Средняя численность популяции не зависит от начальной численности, но зависит от коэффициентов системы» [2].

Докажем второй закон, основываясь на методе из [2], для этого вычислим среднее значение количества хищников и жертв для произвольной фазовой кривой в положительном квадранте.

Произведем для удобства замену . Перепишем исходную систему в виде:

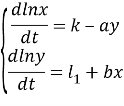
Проинтегрируем первое уравнение на промежутке [0;T], где T –период колебаний.

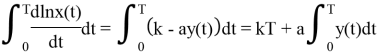
Учитывая формулу Ньютона — Лейбница, свойства интеграла [4] и свойства периодических функций:

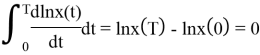
Получаем:

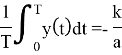
Аналогично, интегрируя второе уравнение:

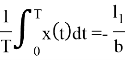
Второй закон Вольтерры доказан.

Выводы:

1. Фазовые кривые системы уравнений Лотки-Вольтерра замкнуты
2. Численность популяций хищников и жертв меняется периодически
3. Период колебаний зависит от начальной численности популяций и коэффициентов системы
4. Средняя численность популяции не зависит от начального значения, но зависит от коэффициентов системы

Литература:

1. Вольтерра В. Математическая теория борьбы за существование. М.: Наука, 1976. 228 с.
2. Соколов С. В. Модели динамики популяций: учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2018. 61 с.
3. Арнольд В. И. Обыкновенные дифференциальные уравнения. –– Новое издание, исправл. –– М.: МЦНМО, 2012. 344 с.: ил.
4. Зорич В. А. Математический анализ. Часть I. — 6-е изд, дополн.— М.: МЦНМО, 2012. — XVIII + 702 с. Библ.: 55 назв. Илл.: 65.