As is known, if the rate of change of the state of the system is much less than the rate of change of external conditions, then the process is nonequilibrium.
The causes that cause the nonequilibrium filtration currents can have different physico-chemical nature, for example, the phenomena of sorption and desorption in a porous medium, phase transformations of hydrocarbon systems, the state of gas-condensate mixtures in a porous medium, deformation of reservoir rocks. When a viscoelastic fluid is filtered in a porous medium, its internal stress tends to an equilibrium value. The characteristic time of transition to the equilibrium state is the relaxation time. The tightening of the transient processes leads to a nonequilibrium flow when moving in separate pores. This type of disequilibrium can be observed in the stationary flow of heavy oil in a capillary with a variable cross section. In this case, the dependence «debit-pressure drop» deviates from rectilinear, which is associated with the appearance of additional resistances due to the relaxation properties of the oil. When viscoelastic oil moves through a porous medium, which is a complex system of channels of irregular shape, elastic stresses arise that increase the effective viscosity. In this case, at the same speed of movement, the effective viscosity of the oil increases with decreasing permeability of the porous medium.
The presence of relaxation properties in the liquid determines the character of the resistance when moving in a porous medium [1–8]. Since the relaxing liquid reacts to a change in conditions with a certain delay, depending on the speed of motion, the character of the resistance will change. When the flow is sufficiently slow, the liquid particles deform slowly, and the liquid has time to «react» to these changes. As the speed of motion increases, the transit time through the constrictions decreases, and the liquid particles do not have time to deform, i.e. the relaxation time decreases [1]. This leads to an increase in drag. In connection with the foregoing, the determination of the relaxation time, the rate of filtration of the nonequilibrium fluid and the production rate is of great practical importance, which is considered in this article.
Keywords: liquid, relaxation time, porous medium, noequilibrium fluid.
When studying the filtration of nonequilibrium liquids It mustbe taken into account that the viscous forces causing resistance are the decisive factor only in the region of low filtration rates and noticeably decrease with its increase. In this case, the predominant role is played by elastic forces, since the liquid does not have time to relax during the transition from one pore to another. This leads to an increase in the effective viscosity, since the drag factor increases faster with increasing speed than the filtration rate. It is proved that the increase in the relative resistance with increasing filtration rate is proportional to the value of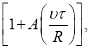 
where
is the relaxation time; R- is the characteristic scale of the change in the cross section; A- is a constant of the order of ten [1]; 
- rate of filtration. Considering that, the 
increase in resistance, expressed through the effective viscosity of the liquid, can be represented as:
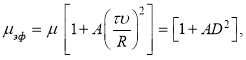(1)
Where 
-is the viscosity of the liquid; D- is the Deborah number, 
[2],- equal to the ratio of the relaxation time of the liquid to the characteristic time of the process.
Thus, in addition to the Re number, the flow is characterized additionally by a new parameter, the Deborah number. For small Deborah numbers, 
the influence of the relaxation properties can be neglected. When 
the head loss is determined not only by the viscosity of the liquid, but also by the parameter
. To quantify this, the filtering law is written in the Darcy form, but with a variable viscosity (effective):
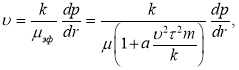(2)
Where a is a constant of the same order as A.
The last relation can be written in the form:
(3)
It follows that the introduction of the cubic term in the approximation 
is connected with the need to take into account the nonequilibrium properties of the filtration flow. Here,
dividing both sides of the equation by a3, we get:
(4)
Let 
, Then we get:
(5)
Substituting in (5)
, we obtain
or
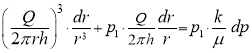(6)
Integrating the left-hand side of this equality from 
and right-hand side from 
we obtain:
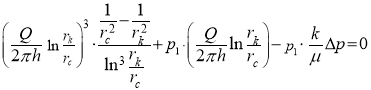(7)
Making a substitution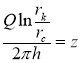
and dividing both sides of the equation by 
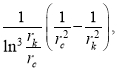we get the equation in the form:
(8)
where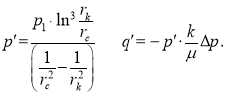
Using the Cardano formula, we find the solution of this equation:
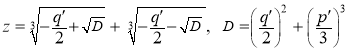(9)
Converting the last expression, we have:
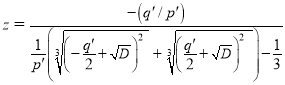(10)
Taking into account that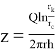 
and - denominator of the right side of the equation, we get:
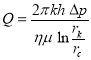(11)
At low speeds 
In the most general form, it can be represented as
To determine 
the dependence is constructed 
, where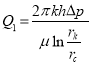 
is under the steady-state filtration regime. The resulting curve is approximated by a polynomial
The relaxation time can be determined by the following formula:
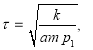(12)
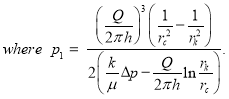(13)
After some transformations, it takes the form:
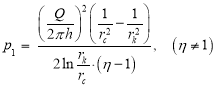, (14)
where 
is found from formula (11). Substituting expression 
from (14) into formula (12), finally for 
we get the expression:
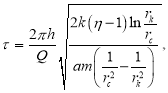(15)
where Q is the instantaneous production rate.
In figures 1–3 graphs plotted for 
and 
depending on the depression 
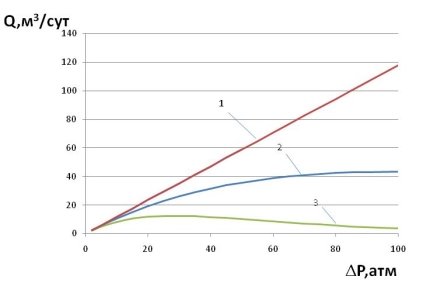
Fig. 1. Curves of changes in debit from depression
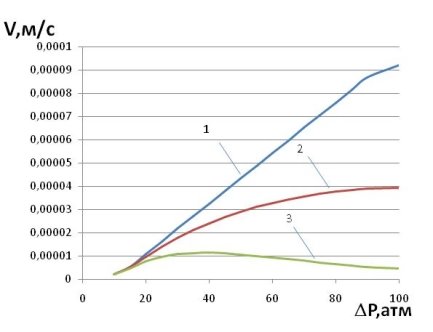
Fig. 2. Curves filtration rate changes from depression
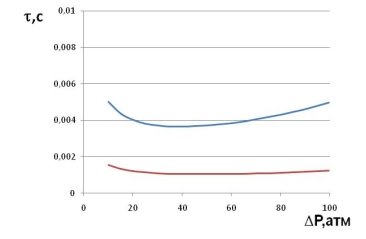
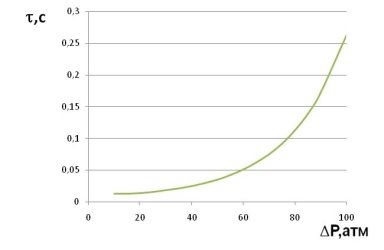
Fig. 3. Curves change the relaxation time from depression
The following data were used in the calculations:
. In each figure for curve 1 
, for curve 2 
for curve 3 
Thus, using the formula (15), we can determine the relaxation time of a nonequilibrium fluid.
References:
- A. Kh. Mirzazhanzadeh, IM Ametov, AG Kovalev. Physics of oil and gas Formation. -Moscow-Izhevsk: Institute for Computer Research, 2005. -280 pp.
- IM Ametov, Yu.N. Baidukov, L. M. Ruzin, Yu. A. Spiridonov. Extraction of heavy and highly viscous oils — Moscow: Nedra, 1985. — 205 s.
- Abasov M. T., Djalilov K. H., Karimov Z. A., Mirzoyeva D. R. On the determination of the parameters of a relaxation-compressible formation, Izv. NAS Azerbaijan. — Ser. Earth sciences. — 2000. — № 2. — P.39–45.
- Abasov MT, Kerimov ZA, Mirzoyeva DR, Kazymova T.Sh. On the Determination of the Parameters of the Creeping and Relaxation-Compressible Formations from the Hydrodynamic Studies of Wells, Izv. NAS Azerbaijan. -Ser.nauk about the Earth. — 2006. — No. 1.-C. 59–64.
- Jalilov KN, Kerimov ZA, Mirzoyeva DR On the filtration of oil to the gallery and borehole in the relaxation of velocity and pressure, Izv. AN Azerb: Ser. Sciences about the earth, 1998, № 2, с.6–12.
- Dunyamaliev MA On a mixed problem for the filtration equation in a relaxation medium. «Bilgi» dərgisi, Baku, 2002, No. 1, p. 9–12.
- Kuliev AM, Efendiev RM, Kazymov BZ, Tagieva E. Influence of the grid density of wells on gas recovery of reservoirs with relaxation collectors. -M.: Neftepromislovoe delo, 2005, No. 11, p.31–34.
- Mirzadjanzade A.Kh., Kuznetsov OL, Basniev K. S., Aliev Z. S. Fundamentals of gas production technology. -Moscow: Nedra, 2003, p.880.
- Molokovich Yu.M. Nonequilibrium filtration and its application in oilfield practice. Publisher: TsentrLitNefteGaz, 2006, p. 214.
