В статье показано выполнение оптимизация диска турбины ГТД по массе в упруго-пластичной постановке задачи в программном комплексе ANSYS Mechanical APDL.
Ключевые слова: оптимизация, снижение массы, диск ГТД, упруго-пластичная задача, ANSYS Mechanical APDL.
Минимальная масса — это одно из основных требований, которым должны отвечать эксплуатируемые в настоящее время авиационные двигатели (АД). Общая масса двигателя складывается из суммы масс отдельных узлов и деталей. Из практики известно, что каждый лишний 1 кг массы двигателя вызывает увеличение массы самолета на 3 кг. Также к важнейшим характеристикам, определяющим совершенство АД, относится удельная масса. В значительной мере эти характеристики определяются конструктивными особенностями турбины. Таким образом, снижая массу диска турбины — ее основного элемента при сохранении других ее характеристик в оптимальном диапазоне можно добиться совершенствования АД.
Исходные данные:
-
Угловая скорость:
;
-
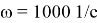Контурная нагрузка:
;
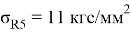- Температура диска от: от 650 до 900 К;
-
Материал: ЭИ-698 ВД (
;
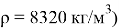- Кривая деформирования сплава ЭИ-698 ВД, представленная ниже (рис. 1).
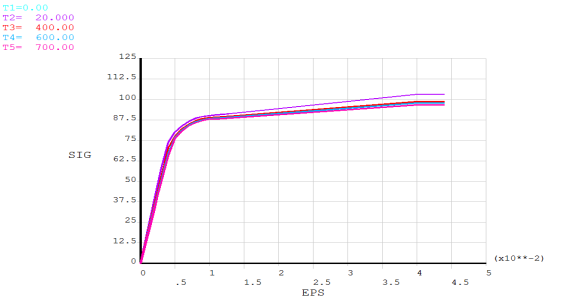
Рис. 1. Кривая деформирования сплава ЭИ-698 ВД
- Модуль упругости, коэффициент Пуассона и условный предел текучести, а также коэффициент температурного расширения для различных температур представлены в таблицах 1–2 соответственно.
Таблица 1
Механические характеристики сплава ЭИ-698 ВД
|
T, К |
293 |
673 |
773 |
873 |
973 |
1073 |
|
E, |
20000 |
18200 |
17500 |
16500 |
15500 |
14300 |
|
μ |
0,3 |
0,3 |
0,3 |
0,3 |
0,3 |
0,3 |
|
|
740 |
- |
700 |
670 |
650 |
570 |
Таблица 2
Коэффициент температурного расширения сплава ЭИ-698 ВД
|
T, К |
293–373 |
293–473 |
293–573 |
293–673 |
293–773 |
293–873 |
293–973 |
293–1073 |
293–1173 |
|
|
11 |
11,4 |
11,7 |
12,1 |
12,4 |
12,7 |
13,4 |
13,9 |
14,7 |
Облик диска турбины представлен ниже (рис. 2).
Оптимизация диска проводится с сохранением ширины 
, радиуса центрального отверстия 
, 
, 
, 
, 
— ширины и радиуса обода.
Варьируемые параметры и диапазон их значений для оптимизации представлены в таблице 3.
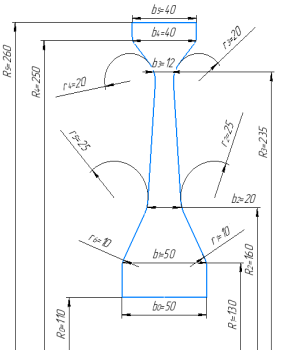
Рис. 2. Облик диска
Таблица 3
Варьируемые параметры
|
Параметр |
|
|
|
|
|
|
|
|
|
Диапазон |
120…135 |
140…170 |
210…245 |
40…60 |
15…25 |
7…15 |
3…35 |
3…25 |
Начинаем работу с создания геометрической модели. Выполняем задание варьируемых параметров: Utility Menu → Parameters → Scalar Parameters. Создаем геометрическую модель, создав последовательно примитивы: точки → линии → скругления, при этом при задании координат точек, используем созданные ранее параметры.
После создаем площади по линиям, вводим характеристики материала, указываем тип и размера элемента (диск — осесимметричное тело, выполненное из одного материала), создаем расчетную сетку. Задаем следующие граничные условия: ограничение по осевым перемещениям (фиксация в точке крепления диска к валу), контурную нагрузку, угловую скорость и температуры, заданные на различных радиусах в соответствии с параболической зависимостью:
, где 
— температура ступицы. Расчетная модель представлена ниже (рис. 3).
Рис. 3. Расчетная модель
Производим расчет. После выполнения расчета приступаем к оптимизации. Целевая функция — объем. Результаты оптимизации представлены ниже (рис. 4 — рис.7).
Лист оптимизации представлен ниже (рис. 8).
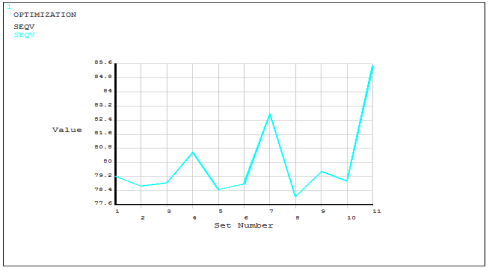
Рис. 4. Эквивалентные напряжения по итерациям
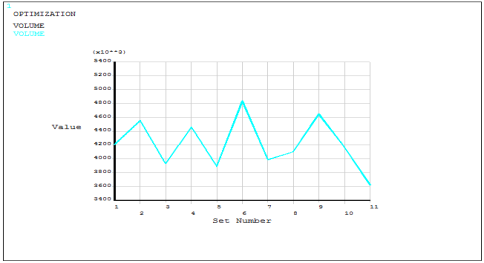
Рис. 5. Объем по итерациям
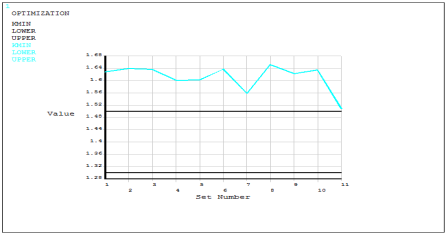
Рис. 6. Коэффициент запаса прочности по итерациям
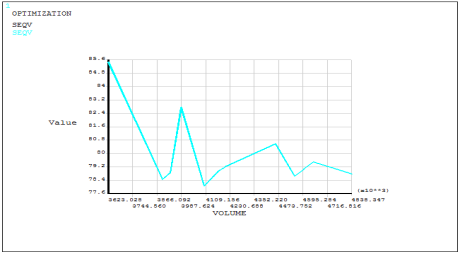
Рис. 7. Эквивалентные напряжения по объемам
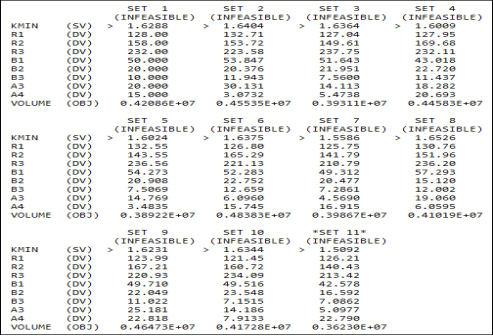
Рис. 8. Лист оптимизации
В качестве конечного варианта выбран полученный в результате 11 итерации. Распределение эквивалентных напряжений этого варианта представлено ниже (рис. 9).
Рис. 9. Распределение эквивалентных напряжений оптимизированного варианта
Заключение: в результате выполнения оптимизации масса диска уменьшилась с 35,016 кг до 30,143 кг, таким образом, масса уменьшилась на 13,92 % при сохранении минимального коэффициента запаса прочности 
, лежащего в диапазоне рекомендуемых значений допускаемых коэффициентов запаса прочности 
.
Литература:
- Галимханов Б. К., Латыпов Р. К. ANSYS: Основы расчета на прочность элементов АД и ЭУ. Методические указания по дисциплине «Конструкция и прочность АД и ЭУ» / УГАТУ, Уфа, 2004 г. — 54с.
- Тархов Л. Н., Харитонов В. Ф. Расчет дисков газотурбинных двигателей. Методические указания к курсовому и дипломному проектированию / УГАТУ, Уфа, 2005 г. — 25с.
- Харитонов В. Ф. Материалы деталей авиационных газотурбинных двигателей. Методические указания к курсовому и дипломному проектированию / УГАТУ, Уфа, 2004 г. — 38с.
