Алгебраические уравнения (двухчленные, трехчленные, многочленные)



Алгебраическим уравнением (неравенством) называют уравнение (неравенство), в левой части которого находится многочлен степени 𝑛 ≥ 0, а в правой — ноль. Многочлен или полином можно рассматривать как сумму одночленов или мономов, каждый из которых представляет собой произведение с числовым коэффициентом нескольких переменных, возведенных в целые неотрицательные степени. Степенью, или порядком, монома называют сумму степеней, входящих в него переменных. Степень многочлена — наибольшая степень входящего в него монома.

Корни двучленного алгебраического уравнения n-го порядка azⁿ + b = 0 находят по формуле z = .

В общем случае для n> 4 не существует формул, выражающих корни алгебраического уравнения через его коэффициенты. Однако справедлив результат, утверждающий наличие корня для любого алгебраического уравнения ненулевой степени.

В простейшем случае при, а=1 имеем хⁿ -1 = 0

Тогда

а) при n= 1 имеем х — 1 = 0 <=> х = 1;

б) при n=2 имеем х² -1 = 0 <=> (х — 1) (х +1) = 0 <=> x₁ =1, х₂ = -1;

в) при n=3 имеем х³ -1 = 0 <=> (х -1) (х² + x + l) = 0<=>x = 1 — единственный действительный корень.

Можно показать, что в общем случае для двучленных уравнений хⁿ — а = 0 справедливы следующие утверждения:

1) при любом положительном, а уравнение хⁿ — а = 0 имеет:

а) при любом нечетном n (n = 2k-1, k∈N) только один действительный корень;

б) при любом четном n (n = 2k, k∈N) только два действительных корня;

2) при, а=0 уравнение хⁿ — а = 0 имеет только один корень х=0;

3) при любом отрицательном, а уравнение, хⁿ-а=0 имеет:

а) при любом нечетном n (n = 2k-1, k∈N) только один действительный корень;

б) при любом четном n (n = 2k, k∈N) не имеет действительных корней.

Пример 1. Решить уравнение.

х^4–625 = 0

Решение:

х^4–625 = 0 ↔ х₁ = = 5, х₂ = - = — 5

Ответ: {-5;5}.

Пример 2. Решить уравнение х^3–27 = 0.

Решение:

х^3–27 = 0 ↔ х³ = 27 ↔ х = = 3.

Ответ: {3}.

Пример 3. Решить уравнение х⁵ -12 = 0.

Решение:

х^5–12 = 0 ↔ х⁵ = 12 ↔ х = .

Ответ: {}.

Пример 4. Решить уравнение х² + 4 = 0.

Решение:

x² + 4 = 0 <=> x² = -4 <=> x є 0.

Ответ: ∅.

Пример 5. Решить уравнение x⁶+ 123 = 0

Решение:

х⁶ + 123 = 0 ↔ х⁶ = -123 ↔ x є 0.

Ответ: ∅.

Пример 6. Решить уравнения: a) x³ = 0; б) x¹² = 0.

Решение:

а) х² = 0 ↔ х = 0.

б) х¹² = 0 ↔ х = 0.

Ответ: а) 0; б) 0.

Трехчленные уравнения. Биквадратные уравнения.

Алгебраическое уравнение вида ах²ⁿ + вхⁿ + с = 0 называется трехчленным, если n≥2, n∈N, а≠0, в≠0, с≠0.

При n=2 трехчленное уравнение ах⁴ + вх² + с = 0 называется биквадратным уравнением.

Заменой переменной xⁿ=t трехчленное уравнение ах²ⁿ + вхⁿ + с = 0 преобразуется в квадратное at² + bt + с = 0.

В частности, для биквадратного уравнения замена х² = t приводит его к квадратному уравнению at² + bt + с = 0.

Пример 1. Решить уравнение x⁴-13x²+36=0.

Решение:

Имеем биквадратное уравнение. Положив x²=t, получим квадратное уравнение t²-13t + 36 = 0 <=> t₁ = 4, t₂ = 9.

Задача свелась к решению уравнений

x² = 4 <=> x₁, ₂ =±2;

x² =9 <=> х₃, ₄ =±3.

Ответ: {±2; ±3}.

Пример 2. Решить уравнение х⁴-3x^2–10=0.

Решение:

Положив x² = t, получаем квадратное уравнение t²-3t-10 = 0 <=> t₁ =-2, t₂ =5.

Теперь задача сводится к решению уравнений х² = -2, х² = 5.

Уравнение х² =-2 не имеет действительных корней, уравнение х² = 5 имеет два корня x₁ =-√5, х₂=√5.

Ответ: {±√5}.

Пример 3. Решить уравнение x^6–3x³+2=0.

Решение:

Имеем трехчленное уравнение. Положив x³=t, получаем

x⁶=(x³)²=t²,

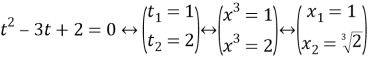
Ответ: {1; ³√2}.

Многочлен степени 𝑛 = 1 называют линейным членом. В курсе математики средней школы мы сталкиваемся также с «многочленами бесконечной степени» [3, c. 63].

Полиномом (многочленом) от переменной называют выражение вида

Где а_i — коэффициенты полинома, a_n ≠ 0 — старший коэффициент, a₀ — свободный член, n — степень полинома.

Если a_n = 1, то полином называется приведённым. Для многочленов определены операции сложения, вычитания, умножения. Операция деления определена не для любой пары многочленов, но, как и для целых чисел, возможно деление с остатком.

Теорема Безу. Остаток от деления многочлена P_n(z) на линейный многочлен z-z₀ равен значению многочлена P_n(z) при z-z₀.

Корнем многочлена P_n(z) называется такое число z = z₀, что P_n(z₀) = 0.

Рассмотрим уравнение

a_nzⁿ + a_n-1z^n-1 + … + a₀ = 0, т. е. алгебраическое уравнение n-ой степени. В некоторых частных случаях корни такого уравнения выражаются через его коэффициенты по определенному правилу.

1. Корни алгебраического уравнения второй степени az² + bz + c = 0 находятся по формуле z_1,2 = 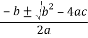, здесь ± 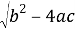— два значения квадратного корня из комплексного числа.
2. Теорема Гаусса (основная теорема алгебры многочленов).

Уравнение a_nzⁿ + a_n-1z^n-1+…+a₁z+a₀=0, где n Є N, a_i Є C, имеет хотя бы один корень (в общем случае комплексный).

Рассмотрим произвольный многочлен P_n(z) ненулевой степени n. Согласно основной теореме алгебры он имеет комплексный корень z₁ и поэтому делится на (z-z₁), т. е. P_n(z) = P_n-1(z)* (z-z₁). Если n-1>0, то многочлен P_n-1(z) имеет корень z₂, тогда P_n-1(z) = P_n-2(z)* (z-z₂), т. е. P_n(z) = P_n-1(z)* (z-z₁)* (z-z₂) и т. д.

Таким образом, из теоремы Гаусса вытекает наличие у многочлена n-ой степени ровно n корней (считая кратные).

Следствие. Многочлен степени n с комплексными коэффициентами и со старшим коэффициентом a_n разлагается в произведение n сомножителей вида (z-z₀), т. е. a_nzⁿ + a_n-1z^n-1+…+a₁z + a₀ = a_n (z-z₁)*(z-z₂)*…(z-z_n), и это представление единственно с точностью до перестановки сомножителей.

В этом разложении некоторые множители могут оказаться одинаковыми, тогда P_n(z) = a_n (z-z₁) ^k1 * (z-z₂) ^k2*…*(z-z_n)^ks, причем k₁+ k₂ + … k_s = n (k_i — кратность корня z_i).

Из свойств сопряженных комплексных чисел вытекают некоторые результаты о корнях многочленов с действительными коэффициентами.

Теорема. Если комплексное число z₀ является корнем многочлена P_n(z) с действительными коэффициентами, то сопряженное число также является корнем этого многочлена.

Доказательство. Из равенства следует равенство =0.

Следствие. Если комплексное число z₀ = a₀ + b₀i, (b₀ ≠ 0) является корнем многочлена P_n(z) с действительными коэффициентами, то этот многочлен делится нацело на квадратный трехчлен z^2–2az + a² + b², также имеющий действительные коэффициенты.

Доказательство. Пусть P_n(z) имеет комплексный корень z₀ = a + b_i, тогда он имеет и корень . Следовательно, P_n(z) делится нацело на (z-z₀)*(z-) = z-a-b_i)*(z-a+b_i) = z^2–2az + a² + b².

Литература:

1. Бронштейн И. Н. Справочник по математике для инженеров и учащихся втузов / И. Н. Бронштейн, К. А. Семендяев. — Москва: Наука, 2015. — 544 с.
2. Корн Г. Справочник по математике для научных работников и инженеров / Г. Корн, Т. Корн. — Москва: Наука, 2014. — 832 с.
3. Королёва Т. М. Пособие по математике для поступающих в вузы. Часть 1 / Т. М. Королёва, Е. Г. Маркарян, Ю. М. Нейман — Москва: Изд-во МИИГА и К, 2015. — 144 с.
4. Курош А. Г. Курс высшей алгебры / А. Г. Курош. — Москва: Наука, 2015. — 432 с.
5. Литвиненко В. Н. Практикум по элементарной математике. Алгебра. Тригонометрия / В. Н. Литвиненко, А. Г. Мордкович. — Москва: Просвещение, 2013. — 352 с.
6. Лунц Г. Л. Функции комплексного переменного / Г. Л. Лунц, Л. Э. Эльсгольц. — Москва: Государственное изд-во физико-математической литературы, 2015. — 300 с.