Статья посвящена описанию методики определения ресурсоемкости проекта, в частности в части трудовых ресурсов некомбинаторным способом, что существенно упрощает вычислительную сложность задачи.
Ключевые слова: управление проектом, теория расписаний, диаграмма Гантта, математическое программирование.
В последние годы всё большую популярность набирают системы позволяющие автоматизировать процессы управления проектом, или осуществляющие поддержку принятия решений. Реализация таких алгоритмов связана с применением теории расписаний. Несмотря на то, что в некоторых случаях задачи теории расписаний являются полиномиальными, многие задачи из теории расписаний относятся к классу NP-полных, что делает их вычислительно трудными. В данной работе рассматривается задача определения количества агентов, необходимых для выполнения полного цикла задач, составляющих проект. Такая оценка может быть полезна для принятия решения при составлении расписаний, или при выборе между несколькими допустимыми расписаниями.
Пусть имеется некий проект, состоящий из N работ, очерёдность и временные промежутки, в которые выполняются работы проиллюстрированы диаграммой Гантта на рисунке 1. Составим алгоритм определения количества сотрудников, необходимых для его выполнения исходя из предположения, что любой работник может быть назначен на любую работу, но только на одну, и для выполнения любой операции достаточно одного работника. Из первого предположения следует, что после завершения любой работы освободившийся сотрудник может быть назначен на любую другую работу, которая начинается не раньше времени завершения этой работы.

Рис. 1. Диаграмма Гантта для проекта, состоящего из 16 задач
Для начала докажем утверждение, о том, что для выполнения всего комплекса работ необходимо и достаточно количества работников, равного максимальному количеству выполняемых работ. Необходимость очевидна, если сотрудников меньше, чем максимальное количество одновременно выполняемых работ, то проект невозможно будет выполнить, так как в определенный момент работ будет больше, чем исполнителей, а по нашему предположению один исполнитель не может выполнять больше одной работы. Докажем достаточность, пусть в момент времени T количество работ максимально, тогда верно следующее утверждение: в любой последующий момент времени t количество работ, завершившихся в промежутке времени [T,t] больше, чем количество работ, начавшихся в этом промежутке. Поскольку завершившихся работ всегда больше, на любую начинающуюся работу всегда можно назначить одного из освободившихся работников. Аналогичные рассуждения можно провести в обратном направлении от T до старта проекта. Достаточность доказана.
Учитывая доказанное утверждение можно предложить алгоритм, определяющий количество работников, необходимых для выполнения совокупности всех работ. Проект в дальнейшем будем представлять в виде сетевой диаграммы в представлении работа — вершина. Матрица связности проекта, представленного диаграммой Гантта на рисунке 1 изображена на рисунке 2.

Рис. 2. Матрица связности для рассматриваемого проекта
Предлагается рассмотреть матрицу связности как оператор, действующий в пространстве расписаний (наборов работ). Компоненты векторов такого пространства означают выполнение или не выполнение агентом с этим расписанием работы, соответствующей номеру компоненты этого вектора. Разумеется, не всякое расписание реально выполнимо. Определим какие действия производит оператор. Действуя оператором на набор работ, получаем новый набор работ — тот, в элементы которого можно перейти из элементов изначального набора. Конструкция вида ![]() показывает количество возможных переходов между элементами вектора x.
показывает количество возможных переходов между элементами вектора x.
Учитывая вышеизложенное, предложим алгоритм, определяющий количество работ, выполняемых одновременно с заданной. Листинг такой функции, реализованной в MathCad приведен на рисунке 3.
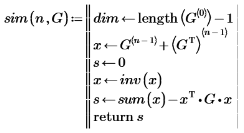
Рис. 3. Листинг функции, определяющей количество работ, выполняемых одновременно с работой n в проекте G
В листинге, приведенном на рисунке 3 использованы функции inv(x) — инверсия булиевого вектора и sum(x) — сумма всех координат вектора. Алгоритм действует следующим образом: выявляются работы, из которых можно перейти в заданную, и работы, в которые можно перейти из заданной. Остальные работы считаются выполняемыми одновременно с заданной, функция возвращает их количество. Далее достаточно найти работу, для которой количество работ, выполняемых одновременно с ней будет максимальным. Листинг этой функции приведен на рисунке 4
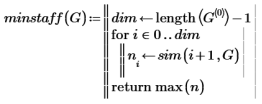
Рис. 4. Листинг функции, определяющей минимальное количество работников, для выполнения проекта G
Число, возвращаемое указанной функцией, и будет минимальным числом работников, необходимых для выполнения всего комплекса работ. Для матрицы связности, приведенной на рисунке 2, функция Minstaff(A) = 6. Действительно, как видно из рисунка 5, наиболее ресурсоемкий момент требует участия 6 работников.

Рис. 5. Диаграмма Гантта рассматриваемого проекта с выделением наиболее ресурсоемкой стадии
Указанный метод может быть использован для уменьшения вычислительной сложности задач оценки эффективности построения расписаний и может применяться для повышения эффективности систем поддержки принятия управленческих решений.
Литература:
- Конвей Р. В., Максвелл В. Л., Миллер Л. В. Теория расписаний. Москва: Главная редакция физико-математической литературы изд-ва «Наука», 1975.
- S. M. Johnson, Optimal two- and three-stage production schedules with setup times included, Naval Res. Log. Quart. I(1954) 61–68.
- Танаев В. С., Гордон В. С., Шафранский Я. М. Теория расписаний. Одностадийные системы.- М.: Наука, 1984.
- Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5–8459–0857–4.







