Решена задача управления дебитом жидкости. Процесс описывается гиперболическим уравнением с начально-краевыми условиями. Процесс управляется давлением или дебитом газа на башмаке. Найдена управляющая функция, зависящая от времени. Построены графики дебита нефти в зависимости от давления и дебита закачиваемого газа, которыми могут руководствоваться нефтяники и газовики. Составлены программы построения таких графиков для каждой скважины в отдельности. Найдены точки оптимума дебита для нефтяных и газовых скважин.
Ключевые слова:газлифт, дебит нефти, дебит газа, давление, закачиваемый расход газа.
Problem of liquid yield control was solved. The process is described by a hyperbolic equation with initial-boundary conditions. The process is controlled by pressure or gas yield on the shoe. A time dependent control function was found. Oil yield charts were drawn depending on the pressure and yield of injected gas, which oil and gas workers could use. Programs were created for drawing such charts for each well separately. Optimum yield points for oil and gas wells were found.
Key words: gas lift, oil flow rate, gas flow rate, pressure, injected gas flow rate.
В статье решены задачи достижение оптимального и максимального дебита с учетом предельного градиента давления нефти управляя минимальной энергией давлением на башмаке. На основании полученного решения построены графики зависимости дебита нефти от давления и дебита закачиваемого газа на башмаке.
Несмотря на то, что газлифтный метод давно известен и широко применяется в нефтяной промышленности различных стран мира [2], строго математически обоснованная теория газлифта до сих пор отсутствует [2,4]. Этот факт является основной причиной применения грубых инженерных расчетов при добыче нефти газлифтным способом, который является существенным ограничением автоматизации этого процесса.
Пусть начало координатной системы находится в верхней точке насосно-компрессорной трубы (НКТ) и ось ![]() направлена вниз по центру окружности поперечного сечения НКТ.
направлена вниз по центру окружности поперечного сечения НКТ.
Неустановившееся движение изотермической газожидкостной среды в вертикальной трубе длиной ![]() и постоянным поперечным сечением
и постоянным поперечным сечением ![]() НКТ описывается следующим дифференциальным уравнением в частных производных [1,2]:
НКТ описывается следующим дифференциальным уравнением в частных производных [1,2]:
![]() +
+![]() +
+![]() ,
,
![]() (1)
(1)
где: ![]() перепад давления стационарной и возмущенной газожидкостной среды;
перепад давления стационарной и возмущенной газожидкостной среды;
![]() средняя скорость смеси по трубе вверх;
средняя скорость смеси по трубе вверх;
![]() — скорость звука в жидкости;
— скорость звука в жидкости;
![]() коэффициент гидравлического сопротивления;
коэффициент гидравлического сопротивления;
![]() плотность смеси, число слагаемых равно числу фаз;
плотность смеси, число слагаемых равно числу фаз;
![]() — ускорение силы тяжести;
— ускорение силы тяжести;
![]() диаметр поперечного сечения;
диаметр поперечного сечения;
![]() предельный градиент давления.
предельный градиент давления.
Систему (1) приведем к следующему виду:
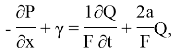
![]() (2)
(2)
где: ![]() .
.
Подстановкой:
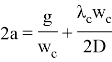
систему (2) можно привести к следующему гиперболическому уравнению (колебательная система):
![]() (3)
(3)
Начальные и краевые условия будут:
![]() (4)
(4)
![]() (5)
(5)
Не ограничивая общности можно положить ![]() Уравнению (3) удовлетворяет и функция
Уравнению (3) удовлетворяет и функция ![]() расход закачиваемого газа и для нее ставится соответствующие начальные и граничные условия.
расход закачиваемого газа и для нее ставится соответствующие начальные и граничные условия.
Пусть процесс описывается уравнением:
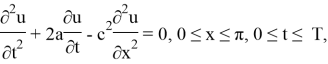
начальные условия:
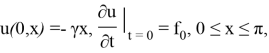
граничные условия:
![]()
![]() условие согласования.
условие согласования.
Решим следующую задачу оптимального управления: При ![]() т. е. чтобы перевести систему за время
т. е. чтобы перевести систему за время ![]() в состояние:
в состояние:
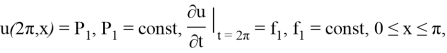
нужно найти управление ![]() при этом:
при этом:
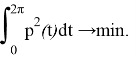
Решая задачу, найдем оптимальную управляющую функцию в следующем виде:
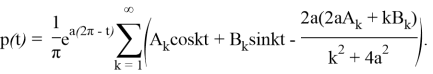
Итак, решение задачи (3)-(5) будет:
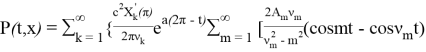 +
+
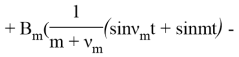
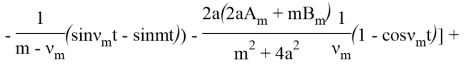
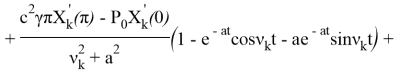
![]() +
+![]() ,
,
где: ![]()
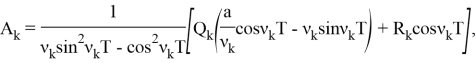
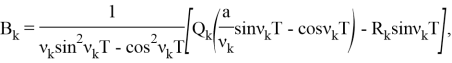
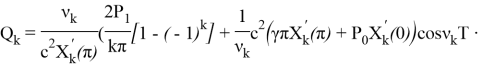
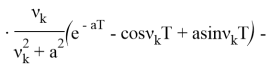
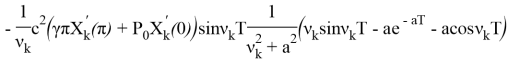
![]()
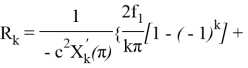
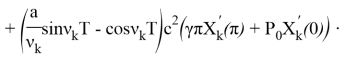
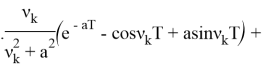
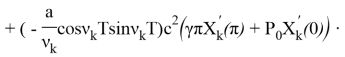
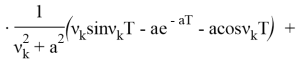
![]()
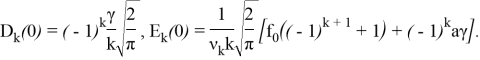
В этой задаче для следующих исходных данных проведены вычисления с использованием математического пакета Maple:
![]()
![]() ;
;![]()
![]() ,
, ![]()
Построены графики оптимальной управляющей функции (рис.1) и решения задачи управления давлением (рис.2). Оптимальные режимы работы газлифтных скважин определяются на основании парабол, показанных на рис.1 и рис.2, которые получены из решения соответствующих задач.
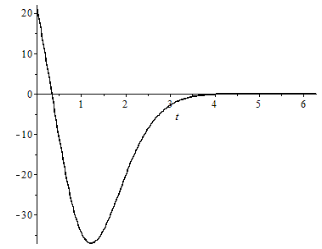
Рис. 1. График управляющей функции дебитом газа
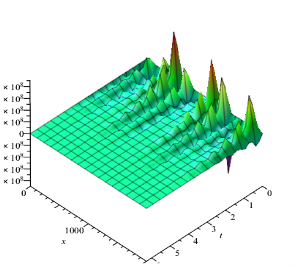
Рис. 2. График решения задачи управления давлением
На основании решения соответствующих задач для исследования дебита каждой скважины строятся параболы, показывающие зависимость дебита скважины от давления и дебита газа:
![]()
![]()
где: ![]() параметры, зависящие от давления,
параметры, зависящие от давления, ![]() параметры, зависящие от дебита газа.
параметры, зависящие от дебита газа.
Оптимальным режимом принято считать тот, который характеризуется минимальным значением удельного расхода закачиваемого газа или координаты точки, где касательная, проходяшая через начало координатной системы, соприкасается с параболой. Почти все известные методы исследова-ния и оптимизации работы газлифтных скважин основаны на анализе этих характеристик. Такой подход требует исследования газлифтных скважин на нескольких режимах работы ее, различающихся темпами закачки газа, что приводит к излишней потере времени, нефти и перерасходу газа [2,4].
Поэтому для нефтяных и газовых компаний имеет практическое значение предварительное теоретическое решение задач по добыче нефти и газа. Эти задачи рассмотрены в [1] без учета предельного градиента давления нефти.
Правая точка пересечения горизонтальной прямой с параболой является оптимальным значением для газовых скважин рис. 3. и рис. 4.
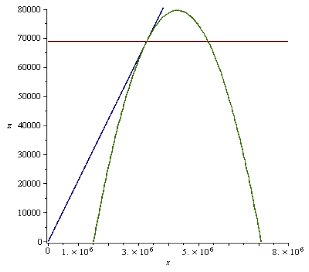
Рис. 3. График зависимости дебита жидкости от давления
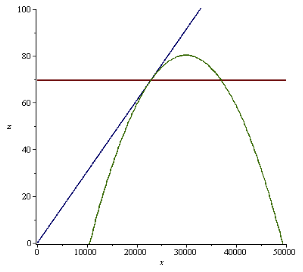
Рис. 4. График зависимости дебита жидкости от дебита закачиваемого газа
Выводы
-
При создании на устье скважины 70 atm с помощью найденной управляющей функции начинается движение газожидкостной смеси в насосно-компрессорной трубе. При
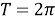 процесс переводится в стационарное состояние. При этом вычислено, что можно добыть нефти за сутки в оптимальном режиме 69,4 т., а максимальном режиме — 80,2 т.
процесс переводится в стационарное состояние. При этом вычислено, что можно добыть нефти за сутки в оптимальном режиме 69,4 т., а максимальном режиме — 80,2 т.
- Полученные численные результаты совпадают с ранее известными промысловыми статистическими данными, а также они показывают на практическую пользу применение теории оптимального управления к нефтедобыче и может служить руководством для нефтянников и газовиков.
Литература:
- Алиев, Ф.А., Ильясов, М.Х., Нуриев, Н. Б. Проблемы математического моделирования, оптимизации и управления газлифта. Доклады НАН Азербайджана, 2009, № 2.
- Мирзаджанзаде, А.Х., Аметов, И.М., Хасанов, А. М. Технология и техника добычи нефти. М.: Недра, 1986.
- Чарный, И. А. Неустановившиеся движения реальной жидкости в трубах. М.: Гостехиздат, 1951.
- Щуров, В. И. Технология и техника добычи нефти. М.: Недра, 1983.

