Моделирование системы «АИН ШИМ – АД» с переменными ψm - is в Matlab и Си



Моделирование системы «АИН ШИМ – АД» с переменными ψ_m - i_s в Matlab и Си

Емельянов Александр Александрович, старший преподаватель;

Бесклеткин Виктор Викторович, старший преподаватель;

Агзамов Игорь Маратович, студент;

Зозулин Михаил Сергеевич, студент;

Зорин Дмитрий Иванович, студент;

Бухряков Иван Федорович, студент;

Онищенко Константин Юрьевич, студент;

Дятлов Олег Алексеевич, студент;

Кадцын Кирилл Павлович, студент;

Лоскутов Владислав Алексеевич, студент

Российский государственный профессионально-педагогический университет (г. Екатеринбург)

В работе [1] приведена математическая модель САР скорости системы «АИН ШИМ - АД» с переменными ψ_m - i_s. В данной работе рассмотрим модель части этой системы (рис. 1) на языке программирования Си.

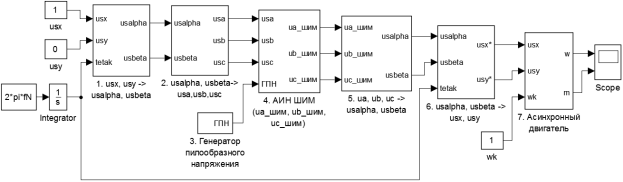
Рис. 1. Математическая модель системы «АИН ШИМ – АД» в Simulink

Для лучшего понимания процесса программирования «АИН ШИМ – АД» на языке Си вначале приведем моделирование этой системы (рис. 1) в Matlab, которая была рассмотрена в статьях в журнале «Молодой ученый» за 2015–2019 гг.

Преобразователи координат u_sx, u_sy → u_sα, u_sβ (номер 1) и u_sα, u_sβ → u_sa, u_sb, u_sc (номер 2) в Simulink приведены на рис. 2 и 3 [2].

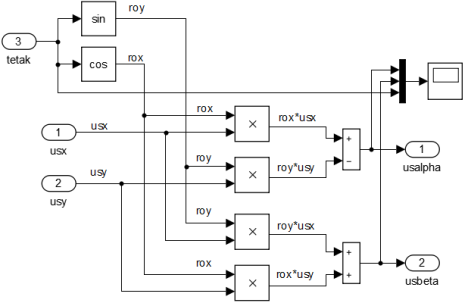
Рис. 2. Преобразователь координат u_sx, u_sy → u_sα, u_sβ

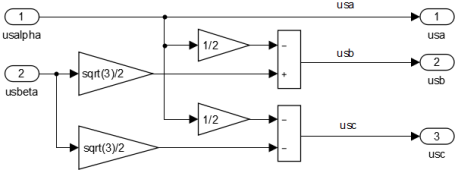
Рис. 3. Преобразователь координат u_sα, u_sβ → u_sa, u_sb, u_sc

Математические модели АИН ШИМ (номер 4) и генератора пилообразного напряжения ГПН (номер 3) в Simulink даны на рис. 4 и 5.

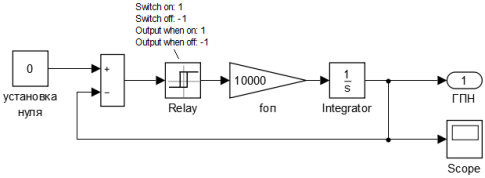
Рис. 4. Генератор пилообразного напряжения (ГПН) в Simulink

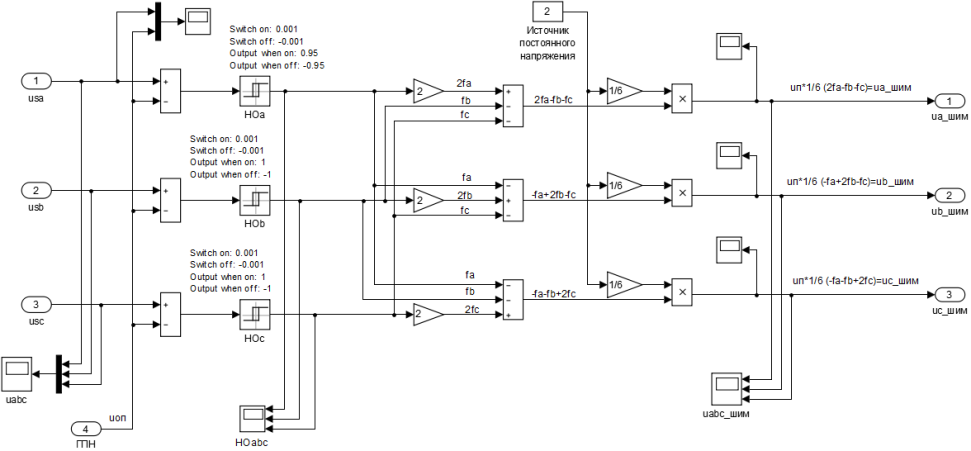
Рис. 5. Математическая модель АИН ШИМ в Simulink

Преобразователи координат u_{а шим}, u_{b шим}, u_{c шим} → u_sα, u_sβ (номер 5) и u_sα, u_sβ → u_sx, u_sy (номер 6) в Simulink даны на рис. 6 и 7.

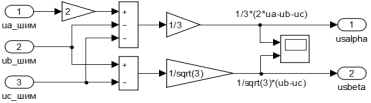
Рис. 6. Преобразователь координат u_{а шим}, u_{b шим}, u_{c шим} → u_sα, u_sβ

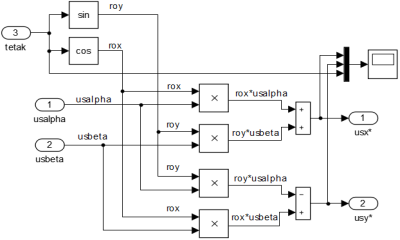
Рис. 7. Преобразователь координат u_sα, u_sβ → u_sx, u_sy

Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными ψ_m - i_sна выходе апериодических звеньев (номер 7) приведена на рис. 9.

Расчет параметров производим в Matlab-Script (рис. 8). Параметры асинхронного двигателя рассмотрены в работах [2] и [3].

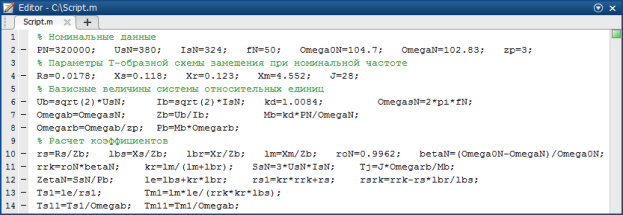
Рис. 8. Расчет параметров модели в Matlab-Script

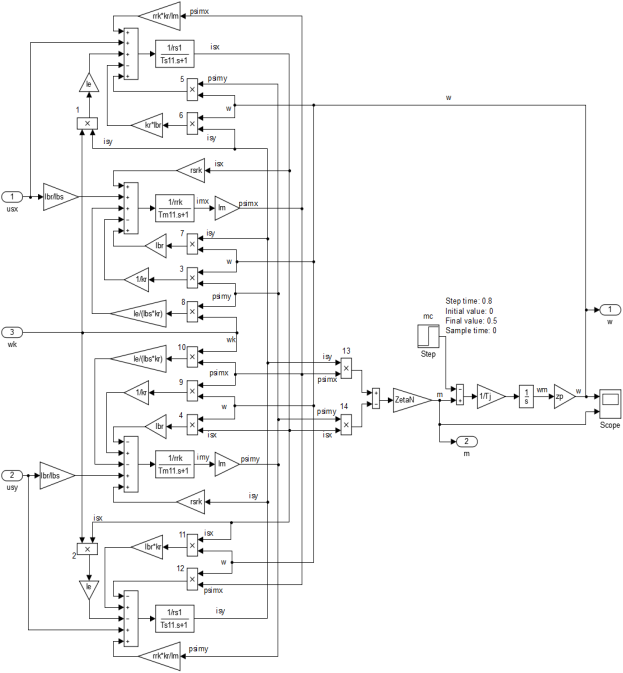
Рис. 9. Математическая модель асинхронного двигателя с переменными ψ_m – i_s на выходе апериодических звеньев в Matlab-Simulink

Результаты моделирования «АИН ШИМ – АД» в Simulink представлены на рис. 10.

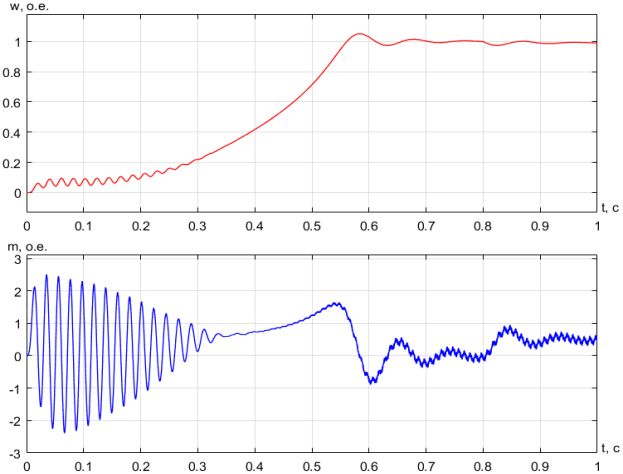
Рис. 10. Графики скорости ω и электромагнитного момента m в Simulink с набросом нагрузки при t = 0,8 с

Математическое моделирование «АИН ШИМ – АД» в Matlab-Script представлено на рис. 11 и 12. Результаты моделирования даны на рис. 13.

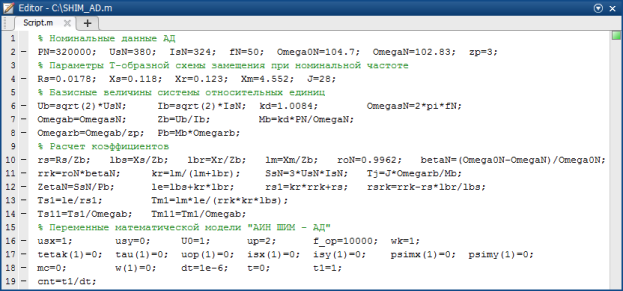
Рис. 11. Задание параметров «АИН ШИМ – АД» в Matlab-Script

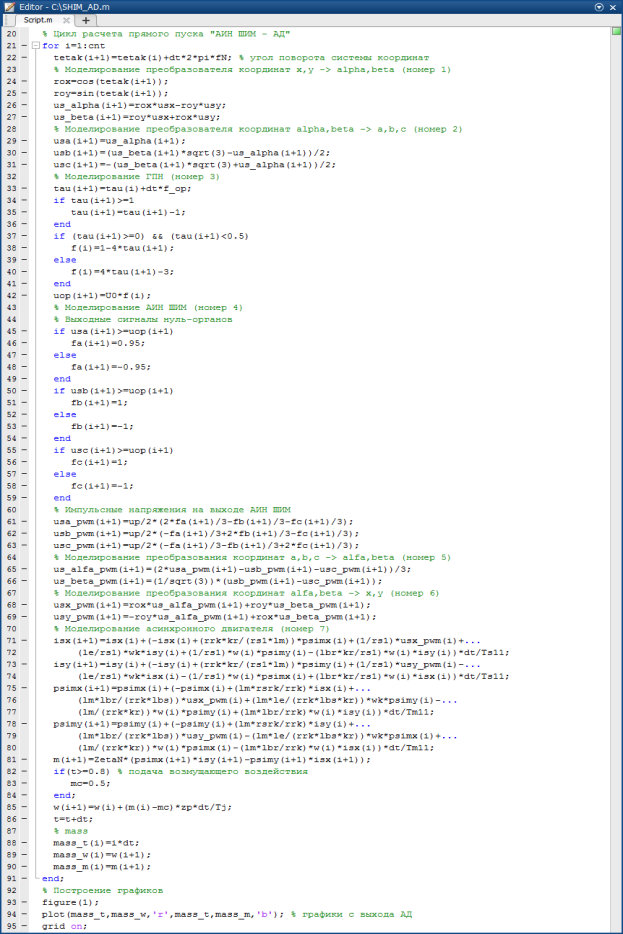
Рис. 12. Цикл расчета «АИН ШИМ – АД» в Matlab-Script

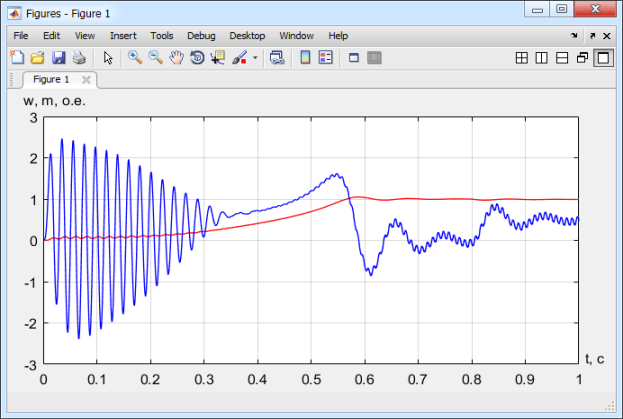
Рис. 13. Графики скорости ω и электромагнитного момента m в Matlab-Script

Программирование «АИН ШИМ – АД» на языке Си приведено на рис. 14 и 15.

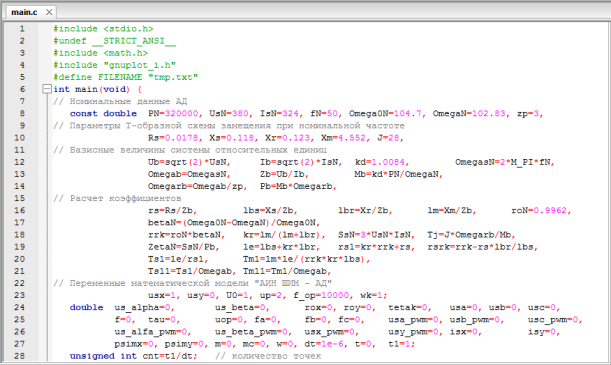
Рис. 14. Задание параметров «АИН ШИМ – АД» на языке Си

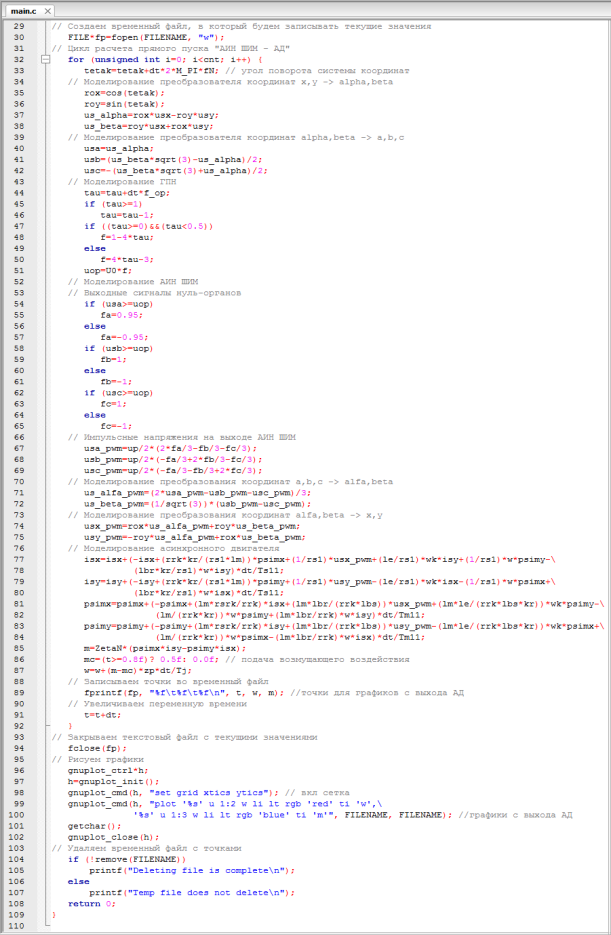
Рис. 15. Цикл расчета «АИН ШИМ – АД» на языке Си

Результаты моделирования «АИН ШИМ – АД» на Си даны на рис. 16.

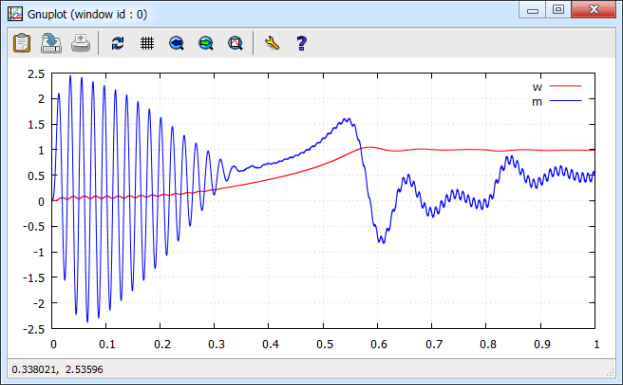
Рис. 16. Графики скорости ω и электромагнитного момента m на языке Си

Литература:

1. Емельянов А.А., Бесклеткин В.В., Соснин А.С., Сучков А.В., Пестеров Д.И., Забузов Е.И., Волков Е.Н., Камолов И.И. Моделирование САР скорости системы «АИН ШИМ - АД» с переменными ψm - is с контуром потока в системе относительных единиц // Молодой ученый. - 2018. - №45. - С. 1-20.
2. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург: УРО РАН, 2000. - 654 с.
3. Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.
4. Васильев А.Н. Программирование на C++ в примерах и задачах. – М.: Издательство «Э», 2017. – 368 с.