Рассматривается неоднородное линейное рекуррентное соотношение (ЛРС) второго порядка с постоянными коэффициентами и произвольной неоднородностью. Выводится аналитическая формула общего члена этого соотношения. Результат иллюстрируется примерами.
Ключевые слова: линейные рекуррентные соотношения, неоднородные, второй порядок, решение, дифференцирование, определитель, второй порядок.
Введение
Рассматривается ЛРС второго порядка
![]() (1)
(1)
где a,b,c — заданные постоянные, ![]() ,
, ![]() — заданная последовательность, определенная при каждом
— заданная последовательность, определенная при каждом ![]() .
.
Рекуррентным соотношением задается модель, описывающая развитие популяции [1]; модель, описывающая распределение государством денежной массы по денежным агрегатам [2] и т. д.
Известно решение ЛРС с конкретными неоднородностями вида ![]() , где
, где ![]() — некоторый многочлен от
— некоторый многочлен от ![]() [3]. Но в случае произвольных неоднородностей общего решения ЛРС, по-видимому, нет.
[3]. Но в случае произвольных неоднородностей общего решения ЛРС, по-видимому, нет.
В настоящей работе эта задача решена. Полученный результат иллюстрируется примерами с конкретными значениями коэффициентов и неоднородности.
- Дифференцирование определителя
При решении задачи нам понадобится следующая теорема.
Теорема 1. Пусть
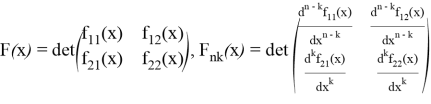 ,
,
где ![]() ,
, ![]() некоторые непрерывно дифференцируемые достаточное количество раз функции.
некоторые непрерывно дифференцируемые достаточное количество раз функции.
Тогда имеет место следующая формула
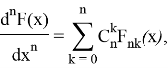
где ![]() — биноминальный коэффициент.
— биноминальный коэффициент.
Замечание 1. Отметим, что при ![]() этот результат общеизвестен [4].
этот результат общеизвестен [4].
Доказательство. Докажем утверждение методом математической индукции по n. Действительно, при ![]() это утверждение верно. Пусть оно верно для
это утверждение верно. Пусть оно верно для ![]() . Тогда для
. Тогда для ![]() имеем:
имеем:
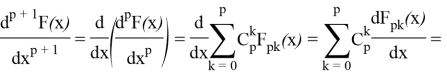
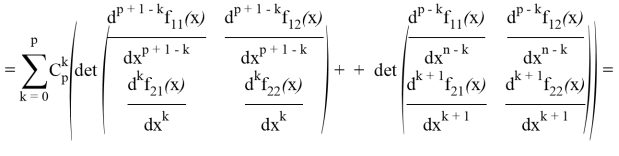
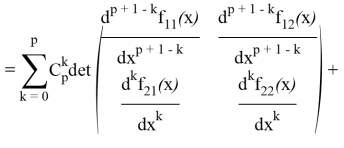
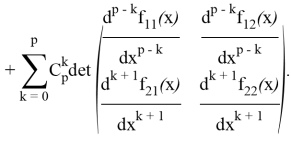
В первой сумме выделим слагаемое с ![]() , а во второй сумме заменим
, а во второй сумме заменим ![]() и выделим слагаемое с
и выделим слагаемое с ![]() :
:
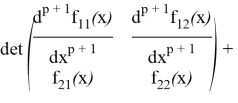
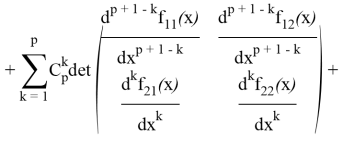
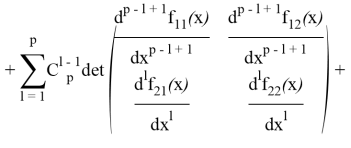
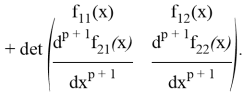
Второе и третье слагаемые внесем под одну сумму; в силу тождества [5]
![]()
получим в ней
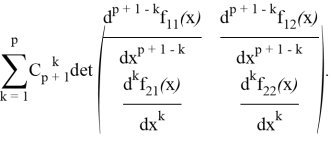
А все выражение равно
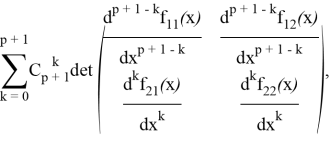
что и требовалось доказать.
- Решение ЛРС
Перейдем к решению ЛРС (1).
Пусть ![]() — некоторые достаточное количество раз непрерывно дифференцируемые в точке
— некоторые достаточное количество раз непрерывно дифференцируемые в точке ![]() функции.
функции.
Вводится функционал ![]() , определяемый формулой:
, определяемый формулой:
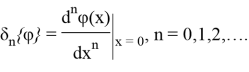
Нетрудно видеть, что для него справедливы следующие теоремы.
Теорема 2. Для любых постоянных ![]() и функций
и функций ![]() справедливо свойство:
справедливо свойство:
![]()
Теорема 3. Для любых функций ![]() справедлив аналог формулы Лейбница:
справедлив аналог формулы Лейбница:
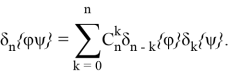
Рассматривается дифференциальное уравнение
![]() (2)
(2)
с некоторой непрерывно дифференцируемой в точке ![]() функцией
функцией ![]() . Продифференцируем его n раз:
. Продифференцируем его n раз:
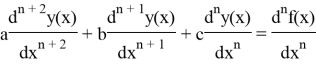
и возьмем ![]()
![]() (3)
(3)
В силу единственности производной, сравнивая (3) и (1), имеем:
![]()
![]()
что влечет взаимно однозначное соответствие между y и ![]() , определяемое формулами:
, определяемое формулами:
![]() (5)
(5)
Решение однородного уравнения для уравнения (2) раскладывается по базису ![]() [6]:
[6]:
![]()
Метод вариации произвольных постоянных приводит к решению
![]()
где
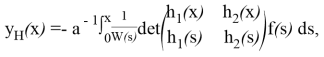 (6)
(6)
в обозначении ![]() ‒ вронскиан, построенный по функциям
‒ вронскиан, построенный по функциям ![]() .
.
Имеет место следующая теорема.
Теорема 4. Решение ЛРС (1) представимо в виде
где ![]() — решение однородного ЛРС.
— решение однородного ЛРС.
Вычислим слагаемые этого решения. Применив утверждение теоремы 1, получим решение однородного ЛРС:
![]() (8)
(8)
Для вычисления ![]() продифференцируем n раз функцию
продифференцируем n раз функцию ![]() , определяемую формулой (6); применим для этого утверждение теоремы 1 и сгруппируем слагаемые по производным функции
, определяемую формулой (6); применим для этого утверждение теоремы 1 и сгруппируем слагаемые по производным функции ![]() :
:
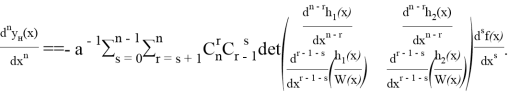
Тогда, применив функционал ![]() , и учитывая (5), имеем:
, и учитывая (5), имеем:
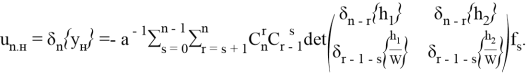 (9)
(9)
Таким образом, с применением равенства (4), утверждений теорем 2 и 4, получен следующий результат.
Теорема 5. Общее решение ![]() ЛРС (1) равно (7), где
ЛРС (1) равно (7), где ![]() определяется формулой (8), а
определяется формулой (8), а ![]() ‒ формулой (9).
‒ формулой (9).
- Базисная система последовательностей для ЛРС (1).
Рассмотрим характеристическое уравнение
Пусть ![]() — его корни,
— его корни, ![]() — его дискриминант.
— его дискриминант.
Выпишем базисные функции:
1) при ![]() уравнение имеет различные корни; базисные функции таковы:
уравнение имеет различные корни; базисные функции таковы:
![]()
2) при ![]() уравнение имеет корень
уравнение имеет корень ![]() и базисные функции
и базисные функции
![]()
3) при ![]() оно имеет два комплексно сопряженных корня
оно имеет два комплексно сопряженных корня
![]() ; при этом базисные функции равны
; при этом базисные функции равны
![]()
По аналогии с базисной системой функций введем следующее понятие.
Определение. Назовем базисной систему последовательностей
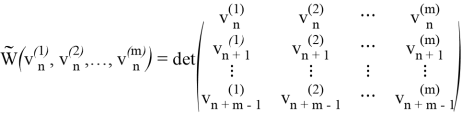
отличен от нуля.
Базисные последовательности для ЛРС (1) определяются по формулам:
![]() .
.
В каждом случае, применив утверждение теоремы 3, имеем:
1) при ![]() ; (10)
; (10)
2) при ![]() ,
, ![]() ;
;
3) при ![]() ,
,
![]() ,
,
где mod обозначается остаток от деления, ![]() ‒ целая часть числа
‒ целая часть числа ![]() .
.
Проверим, к примеру, что система (10) является базисной. Действительно, по определению,
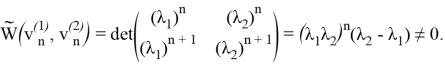
Остальные случаи проверяются аналогично.
- Примеры
Пример 1. Решить ЛРС
![]()
1) Характеристическое уравнение
![]()
имеет корни
![]()
2) Базисная система последовательностей для этого ЛРС такова:
![]()
3) Однородная часть решения ЛРС равна
![]()
4) Формула (9) дает выражение для неоднородной части решения:
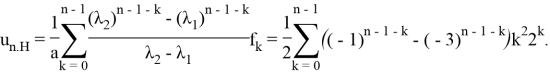
Общее решение ЛРС, в силу теоремы 5, — это ![]() .
.
Замечание 2. Если в сумме верхний предел меньше нижнего, то слагаемые суммы полагают равными нулю.
Сделаем проверку. Взяв в ЛРС, к примеру, ![]() , получим верное тождество:
, получим верное тождество:
![]()
![]()
![]()
Пример 2. Решить ЛРС
1) Характеристическое уравнение
![]()
имеет корень
![]()
2) Базисная система последовательностей для этого ЛРС такова:
![]()
3) Однородная часть решения ЛРС равна
![]()
4) Формула (9) дает выражение для неоднородной части решения:
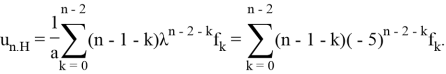
Общее решение ЛРС — это
Сделаем проверку. Взяв в ЛРС, к примеру, ![]() , получим верное тождество:
, получим верное тождество:
![]()
![]()
![]()
![]()
Литература:
- Неверова Г. П., Абакумов А. И., Фрисман Е. Я. Режимы динамики лимитированной структурированной популяции при избирательном промысле // Математическая биология и биоинформатика. 2017. ‒ Т. 12, № 2. ‒ С. 327–342.
- Денежная масса и её структура [электронный ресурс]. ‒ Режим доступа: https://studopedia.ru/19_286070_denezhnaya-massa-i-ee-struktura.html (дата обращения: 03.10.2019).
- Воронин В. П., Поспелов А. Д. Дополнительные главы дискретной математики. — М.: МГУ им. М. В. Ломоносова, 2002. — 129 с.
- Вронскиан [электронный ресурс]. — Режим доступа: https://ru.wikipedia.org/wiki/ Вронскиан (дата обращения: 12.10.2019).
- Биноминальный коэффициент [электронный ресурс]. — Режим доступа: https://ru.wikipedia.org/wiki/Биноминальный_коэффициент (дата обращения: 18.09.2019).
- Понтрягин Л. С. Обыкновенные дифференциальные уравнения. — М.:Наука, 1974. — 331 с.







