Сравнение поведения твердотельно смоделированной арки из вальцованного U-образного профиля с результатами экспериментальных данных из вальцованных металлических тонкостенных профилей при действии ветрового давления.
Ключевые слова: вальцованный U-образный профиль системы MIC-120, деформации арок, ветровая нагрузка, арка, свод, компьютерное моделирование.
To Compare the behavior of a solid-state modeled arch from a rolled U-shaped profile with the results of experimental data from rolled metal thin-walled profiles under the action of wind pressure.
Keywords: rolled U-shaped profile of MIC-120 system, deformation of arches, wind load, arch, arch, computer modeling.
Сравнив результаты перемещений, полученных экспериментом с численными результатами оболочки с приведенным Т-образным сечением, получили отличия в 36 %, что не приемлемо [3]. Смоделируем U образный вальцованный арочный профиль для сравнения с экспериментальными данными.
Материалы и методы: смоделировали U образный вальцованный арочный профиль для сравнения с экспериментальными данными пролетом 18 м при действии ветра 9 м/с. Смоделируем арку с учетом гофрировки стенок и полки для численного анализа. Модель арки закреплена из плоскости в верхних гранях, отражай воздействие соседних профилей. Закрепления модели примем как шарнирные, ввиду идеализацией опорных закреплений свода, которые, скорее всего, обладают упругой податливостью поворота вследствие тонкостенности вальцованных профилей [3].
Ветровую нагрузку берем из численного расчета в программном комплексе, определенной по обдуванию свода из Т образных профилей в аэродинамической трубе по аналогии с ранее проделанными моделями [1], [4], [5]. Величины полученных ветровых давлений по зонам при скорости ветра 9 м/с соответственно: ![]() = 18,77 Па,
= 18,77 Па, ![]() = -39,36 Па,
= -39,36 Па, ![]() = -5,96 Па., Проведем численный расчет модели методом конечных элементов [2]. Полученные результаты перемещений и деформаций показаны на рисунках 1,2.
= -5,96 Па., Проведем численный расчет модели методом конечных элементов [2]. Полученные результаты перемещений и деформаций показаны на рисунках 1,2.
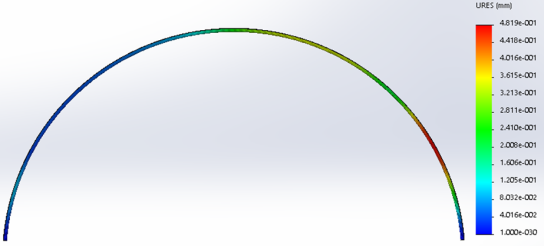
Рис. 1. Результат перемещений арки, полученных твердотельным моделированием пролетом 18м.

Рис. 2. Результат деформаций арки, полученных твердотельным моделированием пролетом 18 м.
Экспериментально полученные результаты максимальных перемещений и деформаций показаны на рисунке 3 [3].
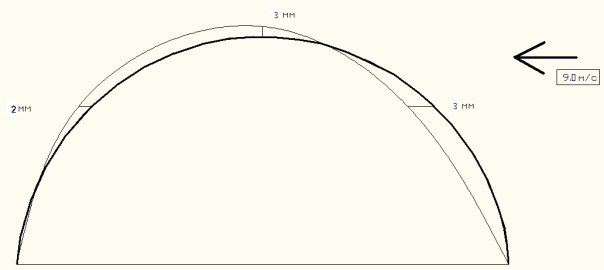
Рис. 3. Максимальные перемещения точек свода, полученные экспериментально [3]
Максимальное перемещение свода, полученное экспериментально при скорости ветра 9м/сек, составило 3 мм, как показано на рис.3. Максимальное же перемещение, полученное в результате моделирования ветровой нагрузки на свод и дальнейшего конечно-элементного расчета, составило 0,5 мм при той же скорости ветра.
Сопоставив результаты твердотельного моделирования гофрированной арки с экспериментальными данными по трем точкам формы деформаций близки. Разница в результатах перемещений объясняется, с одной стороны, динамической ветровым воздействиями раскачивающим тонкостенную конструкцию и, с другой стороны, жесткость экспериментального свода из плоскости не обеспечена диафрагмами жесткости и имеет податливость. В численном расчете учитывалось жесткое закрепление из плоскости уменьшающее перемещения тонкостенной конструкции, обратное наблюдалось при экспериментальном исследовании. Если рассчитать арку без закрепления из плоскости получим перемещений превышающие экспериментальные данные и показаны на рис. 4.
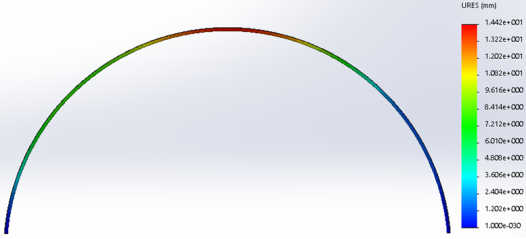
Рис. 4. Результат перемещений арки, полученных твердотельным моделированием пролетом 18м. без закрепления из плоскости
Далее рассчитаем арку с закреплением из плоскости с одной стороны профиля (меньшая полка), эпюры перемещений показаны на рис. 5. Данным расчетом моделируем арку свода, предыдущий профиль держит следующий несимметричный профиль из плоскости.
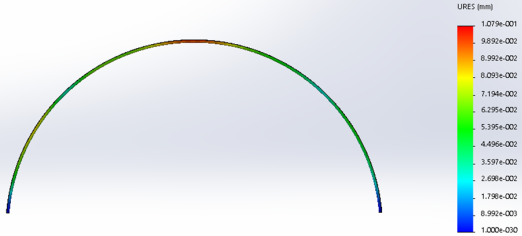
Рис. 5. Результат перемещений арки, полученных твердотельным моделированием пролетом 18м. с закреплением из плоскости с одной стороны профиля
При сравнении перемещений и форм деформаций экспериментальных данных с численным расчетом выявлено влияние жесткости свода из плоскости на перемещения и формы деформаций. Это являет собой предмет дополнительных исследований.
Выводы: сравнили максимальные перемещения и деформации арки по результатам численного расчета модели и экспериментальным данным. Раскрепление из плоскости верхней полки арки-свода для данной тонкостенной конструкции оказывают значительное влияние на увеличение/уменьшение перемещений при воздействии ветрового давления. Ввиду несимметричного сечения профиля закрепление верхних граней из плоскости удерживает стенки профиля вертикально, тем самым включает всю гофрированную стенку в работу и уменьшает перемещения, как было показано при численном расчете.
Литература:
- Веселев Ю. А., Карабутов М. С. Особенности влияния ветрового потока, действующего на сводчатые покрытия под разными углами// Строительная механика инженерных конструкций и сооружений. -2010.- № 4.-С. 11–18.
- Карабутов М. С. Твердотельное моделирование тонкостенных вальцованных профилей металлических сводов// Материалы международной научно-практической конференции «Строительство-2008», -Ростов н/Д: Рост. гос. строит. ун-т, -2008. -С. 55.
- Веселев Ю. А., Карабутов М. С. Экспериментальное изучение поведения свода из вальцованных металлических тонкостенных профилей при действии ветра и сравнение полученных результатов с результатами компьютерного моделирования обдувания свода ветром// Строительная механика инженерных конструкций и сооружений. -2012. — № 2. –С. 72–77.
- Веселев Ю. А., Карабутов М. С. Результаты компьютерного расчета величины ветровой нагрузки, действующей на свод из вальцованных профилей// Строительная механика инженерных конструкций и сооружений.-2019. том15. № 3. -193–200С.
- Веселев Ю. А., Карабутов М. С. Сравнение поведения свода из вальцованных профилей при загружении ветровой нагрузкой по нормам и нагрузкой, полученной компьютерным моделированием// Строительная механика инженерных конструкций и сооружений. -2012. -№ 1, -С.74–80.

