Человек зачастую сталкивается с разными областями деятельности, где встречается большое число задач, решение которых сводится к ОДУ. В данной статье рассматриваются определённые функциональные характеристики физических величин (температура, масса, время, давление и т. д.). Также приведены примеры различных по содержанию задач, решение которых приводится к одинаковым или сходным ДУ.
Ключевые слова: обыкновенные дифференциальные уравнения, общее решение, начальное условие, интегралы по частям.
Пример 1 (размножение бактерий).
В благоприятных для размножения условиях находится некоторое количество 
бактерий. Из опыта известно, что скорость размножения бактерий прямо пропорциональна их количеству. Найти зависимость роста числа бактерий с течением времени.
Решение.
Пусть t — время; R(t) — количество размножающихся бактерий в момент времени, с которого начинается размножение бактерий. Отвлекаясь от того, что значения R(t) являются натуральными числами, будем считать, что функция R(t) непрерывно-дифференцируема при 
. Тогда за достаточно малый промежуток времени 
будем иметь
где 
и коэффициент k зависит от вида бактерий и условий, в которых они находятся, его определяют экспериментально; 
— среднее значение количества размножающихся бактерий за промежуток времени от t до 
, 
при 
. Поделив обе части равенства (1) на и перейдя к пределу при , получим дифференциальное уравнение
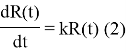
Разделяя в (2) переменные и интегрируя, находим
.
Отсюда
Формула (3) определяет общее решение уравнения (2). Пользуясь начальным условием 
, найдём значение постоянной 
. Подставляя найденное значение С в (3), получим искомый закон размножения бактерий
Следует подчеркнуть, что найденный закон роста бактерий годится только для идеальных условий, т. е. сообщество бактерий располагает неограниченными ресурсами питания и не подавляется никакими средствами, кроме собственной гибели. В реальных условиях, когда уже учитывается недостаток пищи, внутренняя конкурентная борьба внутри популяции и другие факторы, закон изменения роста числа бактерий определяется по-другому.
Пример 2 (рост денежных вкладов в банке).
Сумма 
0 рублей положена в банк под x % в год. Найти закон изменения суммы при условии, что приращение (т. е. проценты) начисляются непрерывно с течением времени t.
Решение.
Общая сумма
вклада в результате начисления x % один раз в конце года составит
Если проценты начисляются по истечению полугодия, то
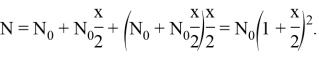
Если поквартально, то
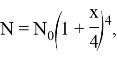
если ежемесячно, то
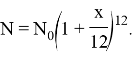
В случае при начислении m раз в год общая сумма составит
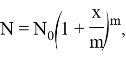
а по истечении n лет
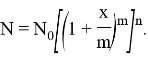
Если число m начислений процентов в год неограниченно увеличится, то
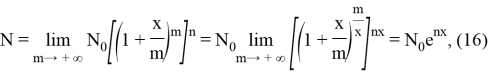
Т. к. 
. Заменяя в (16) n через t, получим сумму, накопившуюся по истечении времени t
В течение короткого промежутка времени dt приращение суммы N равно
которое представляет собой дифференциальное уравнение роста денежных вкладов.
Теперь на основании полученного закона роста (17) рассмотрим следующую частную задачу.
Задача. Сумма 6000 руб. положена в банк под 27 % годовых. Через какое время она составит 18000 руб.? По условию задачи N(0)=N0=6000. Тогда из формулы (17) имеем:
Отсюда
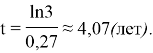
Литература:
- Матвеев Н. М. Методы интегрирования обыкновенных дифференциальных уравнений. Москва — 1967.
- Степанов В. В. Курс дифференциальных уравнений. М., 1958
- Сабитов К. Б. Функциональные, дифференциальные и интегральные уравнения. Москва — 2005.
- Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. М., 1969
- http://booksshare.net/index.php?id1=4&category=biol&author=sabitov-kb&book=2005&page=165
