В работе рассматривается задача нахождения сил и моментов в кинематическом дереве произвольной структуры. Получены замкнутые аналитические выражения сил и моментов через динамические структуры тел.
Ключевые слова: кинематические деревья, робототехника, обратная задача динамики, динамика деревьев тел.
Введение
При построении робототехнических систем часто рассматриваются кинематические цепи тел, соединенных вращательными сочленениями, естественным обобщением данного типа систем тел является система типа кинематического дерева, то есть некоторое количество абсолютно твердых тел, связанных вращательными сочленениями в соответствии с некоторым ациклическим графом — деревом. В данной работе рассматривается задача нахождения сил и моментов, действующих между телами подобной системы.
Обозначения
Определим некоторые функции на графах, которые будем использовать:
-
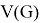 — множество вершин графа
— множество вершин графа 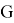 ,
,
-
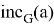 — множество ребер графа
— множество ребер графа 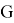 , входящих в вершину
, входящих в вершину 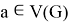 ,
,
-
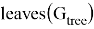 — множество листов дерева
— множество листов дерева 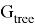 ,
,
-
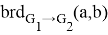 — множество мостов (например — пустое) исходящих из вершины
— множество мостов (например — пустое) исходящих из вершины 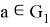 и входящих в вершину
и входящих в вершину 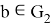 ;
; 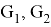 — подграфы
— подграфы 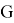 ,
,
-
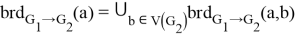 — множество мостов исходящих из вершины
— множество мостов исходящих из вершины 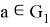 и входящих в любую вершину графа
и входящих в любую вершину графа 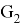 ,
,
-
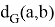 — минимальная длинна пути между вершинами
— минимальная длинна пути между вершинами 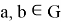 .
.
-
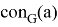 — связная компонента графа, в которую входит вершина
— связная компонента графа, в которую входит вершина 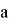 , для ориентированного графа предполагается сильная компонента связности,
, для ориентированного графа предполагается сильная компонента связности,
-
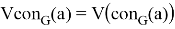 — вершины данной связной компоненты.
— вершины данной связной компоненты.
Уравнения баланса количества движения
Рассмотрим ![]() — множество тел системы. Допустим, что структура связей между телами из множества
— множество тел системы. Допустим, что структура связей между телами из множества ![]() эквивалентна некоторому дереву
эквивалентна некоторому дереву ![]() . То есть если
. То есть если ![]() то между телами
то между телами ![]() имеется связь (сочленение) допускающее их относительное вращательное движение (шарнир). В сочленении действует некоторый момент и некоторая сила реакции. Рассмотрим изоморфный для
имеется связь (сочленение) допускающее их относительное вращательное движение (шарнир). В сочленении действует некоторый момент и некоторая сила реакции. Рассмотрим изоморфный для ![]() ориентированный граф
ориентированный граф ![]() . Введем следующие обозначения:
. Введем следующие обозначения:
-
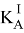 — количество движения тела
— количество движения тела 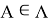 , которое считаем заданным,
, которое считаем заданным,
-
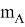 — масса тела
— масса тела 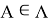 ,
,
-
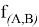 — сила реакции, действующая на тело
— сила реакции, действующая на тело 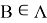 со стороны тела
со стороны тела 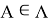 , при этом
, при этом 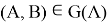 ,
,
-
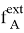 — внешняя сила (по отношению ко всей системе), действующая на тело
— внешняя сила (по отношению ко всей системе), действующая на тело 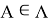 (следует заметить, что, хотя сила тяжести является внешней силой, в данной работе под силой
(следует заметить, что, хотя сила тяжести является внешней силой, в данной работе под силой 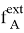 понимается внешняя сила за вычетом силы тяжести).
понимается внешняя сила за вычетом силы тяжести).
Запишем уравнение баланса количества движения для тела A в предположении, что внешние силы действуют только на тела, являющиеся листьями дерева ![]() :
:
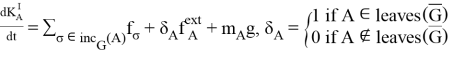 (1)
(1)
Возьмем теперь произвольный лист ![]() . Будем рассматривать подграф
. Будем рассматривать подграф ![]() дерева
дерева ![]() построенный следующим образом:
построенный следующим образом:
![]()
![]()
В граф ![]() входят все вершины, расстояние до которых от заданного листа
входят все вершины, расстояние до которых от заданного листа ![]() не менее фиксированного числа
не менее фиксированного числа ![]() . Так же нам понадобится граф
. Так же нам понадобится граф ![]() расстояния до вершин которого менее
расстояния до вершин которого менее ![]() . Также определим изоморфные ориентированные графы
. Также определим изоморфные ориентированные графы ![]() . Почти очевидно следующее равенство:
. Почти очевидно следующее равенство:
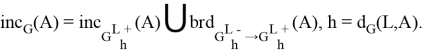
Будем считать, что 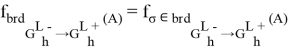 и
и ![]() . С учетом всех замечаний уравнение (1) переписывается в виде:
. С учетом всех замечаний уравнение (1) переписывается в виде:
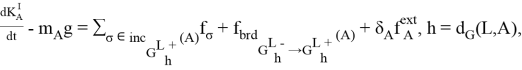 (2)
(2)
На основе (2) получим замкнутую форму уравнений для внутренних сил. Просуммируем (2) по телам ![]() :
:
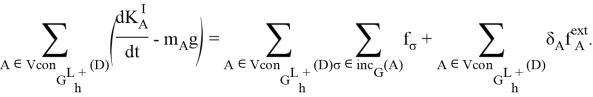
Преобразуем полученное уравнение:
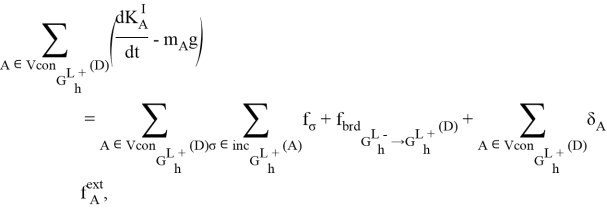
При этом сумма внутренних сил в ![]() равна нулю:
равна нулю:
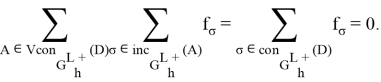
Выразим силу, соответствующую мосту:
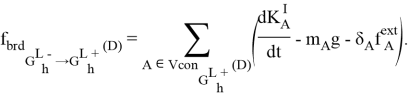
Рассмотрим теперь любое ребро ![]() , такое что
, такое что ![]() , тогда данное ребро является мостом от
, тогда данное ребро является мостом от ![]() к
к ![]() , тогда
, тогда 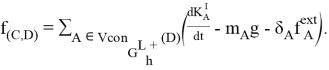 Если же
Если же ![]() , то, используя третий закон Ньютона, получим:
, то, используя третий закон Ньютона, получим: ![]() . Обобщая данный результат, получаем окончательную форму решения:
. Обобщая данный результат, получаем окончательную форму решения:
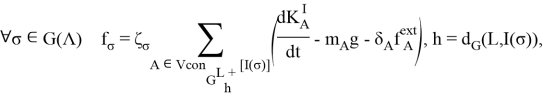
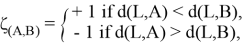
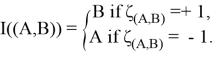
A внешние силы связаны условием, которое не зависит от выбора ![]() :
:
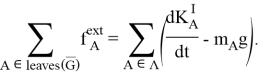
Уравнения баланса кинетического момента
-
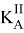 — кинетический момент тела
— кинетический момент тела 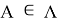 относительно центра масс,
относительно центра масс,
-
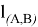 — момент в сочленении, действующий на тело
— момент в сочленении, действующий на тело 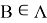 со стороны тела
со стороны тела 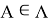 ,
, 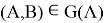 ,
,
-
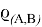 — радиус-вектор неподвижной точки сочленения тел
— радиус-вектор неподвижной точки сочленения тел 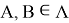 в теле
в теле 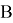 относительно центра масс тела
относительно центра масс тела 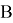 ,
,
-
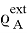 — радиус-вектор относительно центра масс тела
— радиус-вектор относительно центра масс тела 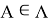 произвольно выбираемой точки приведения внешнего собственно момента,
произвольно выбираемой точки приведения внешнего собственно момента,
-
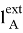 — внешний (по отношению ко всей системе) собственно момент [1], действующий на тело
— внешний (по отношению ко всей системе) собственно момент [1], действующий на тело 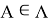 , суть которого заключается в том, что общее моментное действие окружения на тело
, суть которого заключается в том, что общее моментное действие окружения на тело 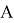 выражается посредством суммы
выражается посредством суммы 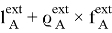 .
.
Сформулируем уравнение баланса кинетического момента для тела ![]() :
:
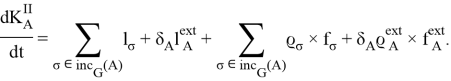
Повторяя те же действия, что и для уравнения баланса количества движения, приводим уравнение баланса момента к следующему виду:
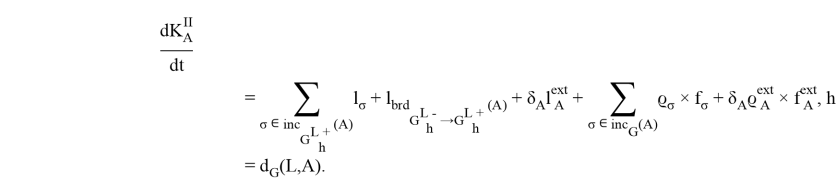
Аналогично предыдущему пункту суммированием по ![]() получаем:
получаем:
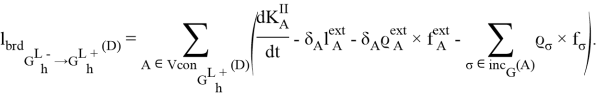
Выражаем решение в общей форме ![]()
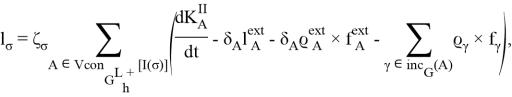
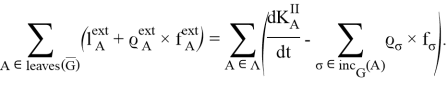
Заключение
Были найдены явные выражения для сил и моментов в кинематическом дереве абсолютно твердых тел. Подробно рассмотрен процесс решения задачи на основе теории графов. Таким образом основным результатом работы являются явные выражения сил и моментов в системе.
Литература:
- Жилин П. А. Динамика твердого тела. СПбГПУ, 2014.
- Жилин П. А. Векторы и тензоры второго ранга в трехмерном пространстве. СПбГПУ, 2012.
- Бабаджанянц Л. К., Пупышева Ю. Ю., Пупышев Ю. А. Классическая механика. Издательство Санкт-Петербургского Университета, 2011.
- Оре О. Теория графов. Наука, 1980.

