Нечеткие множества
Пусть Х универсальное множество, элементы которого обозначены через х. Принадлежность элементов в множестве А из Х часто рассматривается как характеристическая функция 
из Х в {0,1}, т. е.
(1.1)
Множество {0,1} называется множеством оценок.
Если предположить, что не множество {0,1}, а действительный интервал [0,1] является множеством оценок, тогда А будет нечетким множеством. В таком случае 
будет называться функцией принадлежности. Чем больше 
близко к 1. тем больше х принадлежит А [1].
Нечеткое множество А может характеризоваться множеством пар
(1.2)
В общем случае, нечетким множеством 
называется совокупность пар вида 
, где 
(иногда 
— структура типа решетки).
Нечеткое множество может быть конечным и бесконечным. Когда Х-конечное множество, т. е. 
, тогда нечеткое множество на Х определяется следующим образом:
. (1.3)
Когда Х — бесконечное, тогда
(1.4)
Пример. Нечеткое множество А представлено в следующем виде:
A=0.1/1+0.3/2+0.5/3+0.7/4+0.8/5+0.9/6+0.95/7+1.0/8+0.97/9+
+0.9/10+0.8/11+0.7/12+0.5/13+0.3/14+0.1/15.
Тогда классическая версия этого множества имеет вид:
A={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15} или
A=1/1+1/2+1/3+1/4+1/5+1/6+1/7+1/8+1/9+
+1/10+1/11+1/12+1/13+1/14+1/15.
Графическое изображение нечеткого множества А приведено на рис. 1.
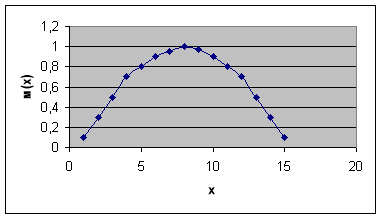
Рис.1. Нечеткое множество
Нечеткое множество может быть представлено в аналитической форме.
Пример.
А= «действительное число близкое к 8»:
.
Нечеткое множество данного типа, т. е. когда функция принадлежности его является обычной (crisp) функцией или степени принадлежности являются обычными числами, называется нечетким множеством 1-го типа. Функция принадлежности нечеткого множества сама может быть нечетким множеством. Тогда нечеткое множество типа 2 определяется как [2,3]
.
Нечетким множеством типа m называется нечеткое множество в Х, у которого значениями функции принадлежности является нечеткое множество типа m-1.
В [4,5] рассмотрен другой тип нечетких множеств. Когда значение функции принадлежности является случайной переменной. В этом случае вероятностное множество А в Х определяется характеристической функцией
,
где 
— является 
— измеряемой функцией для каждого фиксированного 
.
Имеются и другие расширения нечетких множеств. Если
, 
, для которого условия
,
удовлетворяются, то 
называют максимальным или минимальным значением функции принадлежности 
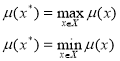(1.5)
Если существует , удовлетворяющего условиям данным выше, то можно рассмотреть следующую задачу: найти последовательность 
из Х таких, что
или (1.6)
.
inf и sup означают наибольшую нижнюю и наименьшую верхнюю границы, соответственно.
Два нечетких множества А и В равны, если их функции принадлежности равны, т. е. если
. (1.7)
Литература:
- Fu H. C., Shann J. J. A fuzzy neural network for knowledge learning // Int. J. Neural Syst.- 1994.- V.5, N.1.- P.13–22.
- Масалович А. И. От нейрона к нейрокомпьютеру // Журнал доктора Добба.-1992.- N.1.- С.20–24.
- Stefanuk V. L. Expert systems and its applications // The lectures of Union's orkshop on the main problems of artificial intillegence and intellectual systems. Part 2, Minsk, 1990.- P.36–55.
