Выделение сигнала на фоне коррелированных помех и некоррелированного шума



В настоящее время широкое распространение получили бесплатформенные инерциальные навигационные системы (БИНС), которые реализуются на микромеханических гироскопах (измерителях угловой скорости) и акселерометрах (измерителях ускорений). Примером аппаратных средств, на которых реализована трёхосная (в трёх пространственных измерениях) БИНС, могут служить микромеханические изделия серии ADIS фирмы Analog Devices [1, 2].

Проблема начальной выставки БИНС дополнительно осложняется вибрациями корпуса носителя навигационной системы. Вибрации могут возникать из-за ветровых воздействий на носитель или вызываться работающими на нём механическими агрегатами. Так, например, если нет возможности провести начальную выставку при выключенных двигателях, то дисперсия сигналов на выходах акселерометров, как показали натурные эксперименты, может возрастать в тысячу и более раз по сравнению с ситуацией, когда двигатели не запущены.

Для подавления шумов акселерометров применяется низкочастотная фильтрация сигналов с их выходов, которая заключается в нахождении математического ожидания оценок, измеряемых по каждой оси ускорений. Подобный подход правомерен, если мешающие компоненты сигналов представляют собой некоррелированный шум [3]. Однако при вибрациях корпуса носителя БИНС предположение о некоррелированности мешающих компонент становится неверным [1].

Представим сигнал в виде:

x(t) = c(t) + s(t) + n(t),

где x(t) — наблюдаемый сигнал; c(t) — коррелированная помеха; s(t) — полезный сигнал; n(t) — некоррелированный шум.

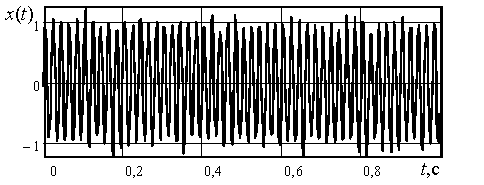
Рис.1. Наблюдаемый сигнал

Выделение полезной компоненты s(t) из смеси x(t) сводится к обелению коррелированной мешающей составляющей c(t) и накоплению полезного сигнала на фоне шума n(t). Известно [3], что коэффициенты импульсной характеристики обеляющего фильтра q‑го порядка могут быть найдены из выражения:

w=R⁻¹ i,

где w= [W₀; W₁; …; Wq] — вектор коэффициентов импульсной характеристики обеляющего фильтра (ОФ), R⁻¹ — [(q+1)×(q+1)]‑мерная корреляционная матрица мешающего процесса, i= [1; 0;…; 0]^T — крайний левый вектор-столбец единичной матрицы.

Структурная схема системы обработки сигнала x(t) представлена на рисунке 2. На нём использовано дискретное представление сигналов:

x_n=x(t), y_n=y(t), s_n=s(t).

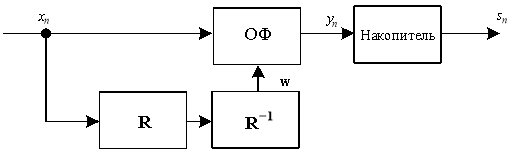
Рис.2. Система обработки акселерометрического сигнала

Выходной сигнал yn на выходе обеляющего фильтра сводится к виду:

yn=,

где y_n — результат обеления; x_n — входной сигнал; W_k — k‑й коэффициент импульсной характеристики w ОФ, k=0, 1, …, q.

Предлагаемый метод обработки выходных сигналов акселерометров подразумевает наличие коррелированной помехи c(t), вызванной дрожанием корпуса носителя БИНС. Помеха c(t) имеет регулярный колебательный характер, действующий по гармоническому закону. На рисунке 3 изображены нормированные к своим максимальным значениям квадраты амплитудно-частотные характеристики S(f) предлагаемого (сплошная жирная линия 3) и известного (пунктирная линия 1) фильтров обработки.

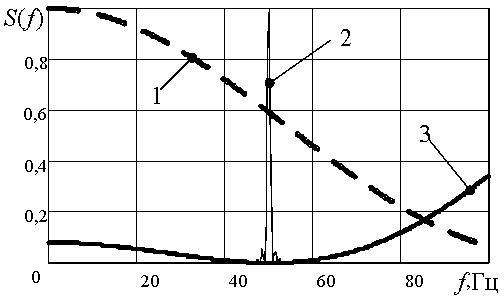
Рис. 3. Частотные характеристики

Под известным фильтром подразумевается равновесный нерекурсивный накопитель q‑го порядка. Кроме того, на рисунке 3 изображена тонкой сплошной линией 2 спектральная плотность мощности S(f) смеси коррелированной помехи c(t) и некоррелированного шума n(t). Порядки фильтров приняты q=3, измеренная доминантная частота f_с коррелированной помехи f_с=50 Гц.

На рисунках 4 и 5 изображены амплитудно-частотные характеристики S(f) для предлагаемого и известного методов при порядках фильтра q=20 и q=40 соответственно

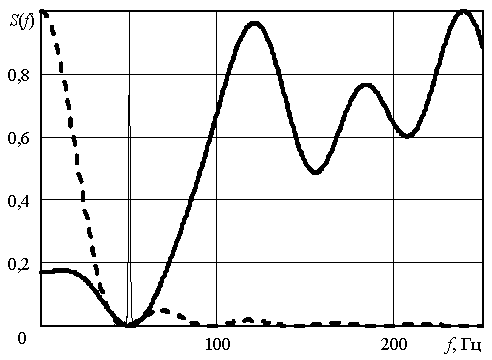
Рис. 4. Частотные характеристики при порядке фильтра q=20

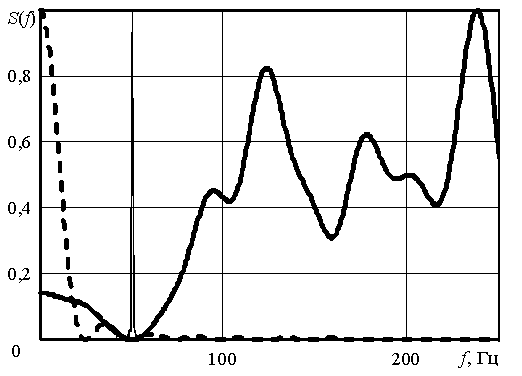
Рис. 5. Частотные характеристики при порядке фильтра q=40

Анализ приведенных на рисунках 3, 4 и 5 зависимостей показывает, что известный подход к обработке акселерометрических сигналов не предусматривает борьбу с коррелированной помехой, т. е. амплитудно-частотные характеристики не имеют провала на частоте воздействия помехи. Предлагаемое решение путём оценивания корреляционных свойств мешающего процесса адаптируется к его частоте и создаёт на ней глубокий провал амплитудно-частотной характеристики. Это даёт возможность подавить мешающую компоненту до уровня шумов, а затем путём накопления сигнала увеличить соотношение сигнал-шум на выходе системы обработки. Предлагаемое решение реализуется путём создания нерекурсивного обеляющего фильтра.

Литература:

1. Андреев В. Г., Белокуров В. А. Метод повышения точности начальной выставки бесплатформенных навигационных систем // Вестник Рязанского государственного радиотехнического университета. № 2. Выпуск 36. 2011. С. 28‑33.
2. Власенко А. Интегральные гироскопы iMEMS + датчики угловой скорости фирмы Analog Devices // Электронные компоненты. № 2. 2003. C. 36‑38.
3. Воробьев С. Н. Цифровая обработка сигналов: Учебник для студентов учреждений высшего профессионального образования. М.: ИЦ Академия, 2013. 320 с.