Метод вариационных итераций и метод разложения Адомиана для нахождения точного решения уравнений некоторых эволюционных уравнений. Получены новые точные решения этих уравнений. Показано, что эти методы являются эффективными и более мощными математическими инструментами для решения линейных и нелинейных дифференциальных уравнений в частных производных.
Ключевые слова: дифференциальные уравнения в частных производных, метод вариационных итераций, метод разложения Адомиана, точное решение.
In this paper, variational iteration method and Adomian decomposition method has been applied to obtain exact solutions of evolution equations. The new exact solutions of these equations have been obtained. It has been shown that the proposed methods provide a very effective, and powerful mathematical tool for solving linear and nonlinear partial differential equations.
Keywords: partial differential equations; variational iteration method; Adomian decomposition method, exact solution.
Математическое моделирование многих реальных нелинейных явлений приводится к дифференциальным уравнениям в частных производных. Особенно эволюционные уравнения появляются в широком диапазоне научного исследования в различных областях механики, физики, прикладной математики. До настоящего времени разработаны многие уникальные методы [1, 2, 5, 6], чтобы исследовать почти все виды эволюционные уравнения и получить их точное решение. Цель данной работы состоит в том, чтобы показать эффективности из этих методов: метода вариационных итераций (МВИ) и метода разложения Адомиана (МРА), возможности легко, быстро и точно решать большой класс задач математической физики.
Пример 1. Требуется приближенно решать следующую задачу с уравнением телеграфа вышесказанными методами (МВИ и МРА) [1, 2]:
(1)
1) По идее МВИ имеем формулу приближенного решения данной задачи:
Здесь 
— множитель Лагранжа, а для стационарного случая 
, 
и отсюда имеем 
.
Применяя МВИ, получим следующие результаты:
; 
; 
;…;
; и т. д.
Точное решение задачи (1):
.
2) Для МРА имеем следующий алгоритм приближенного решения данной задачи [1, 2]:
где 
- дифференциальный оператор;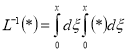 
— интегральный оператор. Применение обратного оператора к заданному уравнению: 
. Основная идея МРА это составление функциональное уравнение вида 
. Отсюда имеем рекуррентное соотношение вида; 
, 
. Аппроксимации: 
; 
; 
; и т. д.
Точное решение задачи (1):
.
Пример 2. Требуется приближенно решать следующую задачу со системой линейных однородных дифференциальных уравнений в частных производных вышесказанными методами (МВИ и МРА) [1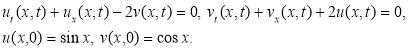, 2]:
(2)
1) По идею МРА имеем формулу приближенного решения задачи (2):
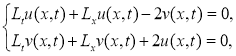
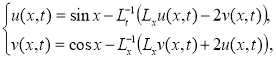
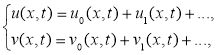
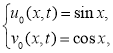
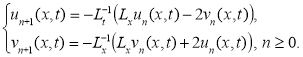
Здесь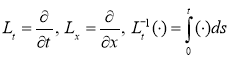 
-операторы. Тогда имеем
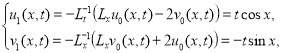
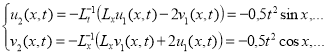
Решение задачи (2):
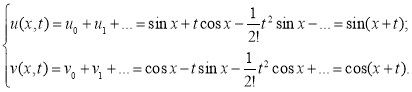
2) По идею МВИ имеем формулу приближенного решения задачи (2):
.
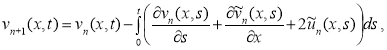
Применяя МВИ, получим 
,
,
и т. д.
Решение задачи (2):
,
.
Пример 3. Требуется приближенно решать задачу с линейным уравнением Клейна-Гордона вышесказанными методами (МВИ и МРА) [1, 2]:
. (3)
1) По идею МВИ имеем формулу приближенного решения задачи (3):
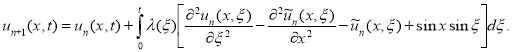
Здесь 
— множитель Лагранжа, а для стационарного случая 
, 
, 
и отсюда имеем 
.
Применяя МВИ, получим следующие результаты:
; 
; 
;…;
и т. д.
Точное решение задачи:
.
2) Для МРА имеем формулу приближенного решения задачи (3):
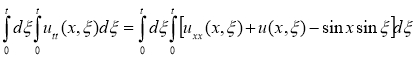
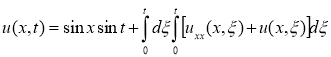
По идею МРА:
;
; 
; 
;
…; 
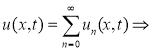
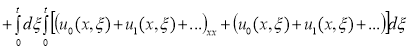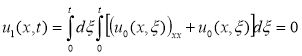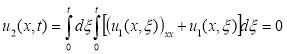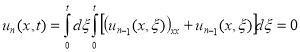и т. д.
Точное решение задачи:
Эти результаты проверены с помощью Maple 17 [7, 8].
Таким образом, МВИ и МРА дают одинаковые результаты, они являются более простим, точным и быстро приближающим к точному решению задачи [2–5]. Поэтому в дальнейшем рекомендуется использование МВИ и МРА при решении линейных и нелинейных задач математической физики.
Литература:
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method. Boston, MA: Kluwer, 1994.
- Wazwaz A. M. Partial Differential Equations and Solitary Waves Theory. Higher Education Press, Berlin Heidelberg, 2009. — 761 p.
- Абдурашидов А. А. Решения нелинейных волновых уравнений методом вариационных итераций // Международный научный журнал: Молодой ученый. — 2017. — № 6. — С. 4–8.
- Абдурашидов А. А., Касимова Ф. У., Рахимова Х. А. Приближенное решение волновых уравнений более высокого порядка методом вариационных итераций // Международный научный журнал: Развитие и актуальные вопросы современной науки, № 4 (4), 2017. — С. 4–9.
- Кудряшов Н. А. Методы нелинейной математической физики: Учебное пособие. 2-е изд. — Долгопрудный: Интеллект, 2010. — 368 с.
- Полянин А. Д., Зайцев В. Ф., Журов А. И. Методы решения нелинейных уравнений математической физики и механики. — М.: ФИЗМАТЛИТ, 2005. — 256 с.
- Эдвардс Ч. Г., Пенни Д. Э. Дифференциальные уравнения и краевые задачи: моделирование и вычисление с помощью Mathematica, Maple и MATLAB. 3-е издание.: Пер. с англ. — М.: ООО «И. Д. Вильямс», 2008. — 1104 с.
- Алексеев Е. Р., Чеснокова О. В. Решение задач вычислительной математики в пакетах Mathcad, Matlab, Maple (Самоучитель). — М.: НТ Пресс, 2006. — 496 с.
