В статье приведены исследование взаимодействия съемника и шпинделя хлопкоуборочного аппарата. Разработан математический модель полноты съема хлопка со шпинделя хлопкоуборочного аппарата.
Ключевые слова: хлопкоуборочные машины, хлопкоуборочный аппарат, щетки, шпиндель, шпиндельный барабан, щеточный съемник
The abstract. In paper research of interacting of the puller and a spindle of the cotton-picking apparatus are resulted. Analysis from a spindle of the cotton-picking apparatus is developed mathematical model of completeness.
Keywords: Сcotton-picking cars, the cotton-picking apparatus, brushes, a spindle, a spindle a drum, a brush the puller
Полноты съема хлопка со шпинделей определяется качеством выполнения процесса съема, которое характеризуется границей зоны очищения поверхности шпинделя. На серийном аппарате установлены два съемника на передней и один на задней паре барабанов. Полнота съема определим по формуле
![]() (1)
(1)
где:
Vo — очищенный объем намотки на шпинделе;
Voб — общий объем намотки на поверхности шпинделя.
Так как Vo = So · H, Voб = Soб · H, то
![]() (2)
(2)
где:
So — очищенная площадь шпинделя;
Soб — общая площадь шпинделя.
Для определения этих площадей рассмотрим схему относительного движения шпинделя и съемника (Рис.1).
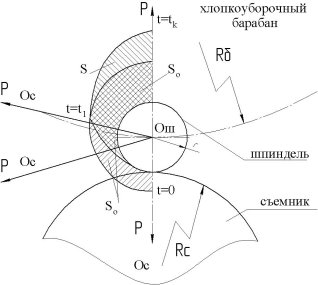
Рис. 1. Схема относительного движения шпинделя и концы щеток съемника
Расстояние между центрами съемника и шпинделя определяется по формуле:
![]() (3)
(3)
Если при повороте шпинделя на угол π расстояние ![]() — r, т. е. между концами щеток и поверхностью шпинделя меньше чем r + d, где d — толщина намотки, то для определения необработанной площадки определим площадь, ограничиваемую кривой концов щеток
— r, т. е. между концами щеток и поверхностью шпинделя меньше чем r + d, где d — толщина намотки, то для определения необработанной площадки определим площадь, ограничиваемую кривой концов щеток
![]() (4)
(4)
где t — время, при котором ![]() = π, т. е.
= π, т. е. ![]() = π /
= π / ![]() . Для упрощения расчетов рассмотрим случай d = 0
. Для упрощения расчетов рассмотрим случай d = 0
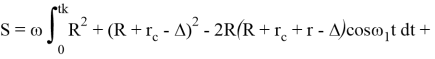
![]() (5)
(5)
Для определения интеграла последнего слагаемого рассмотрим его отдельно. Введем обозначения ![]() = В и
= В и ![]() = А. Тогда
= А. Тогда
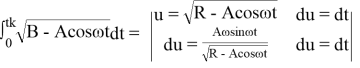 =
=
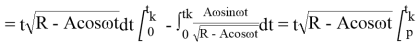 =
=
= 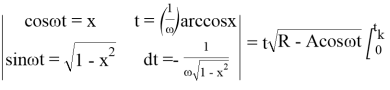 =
=
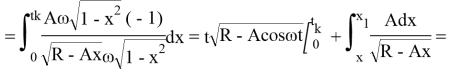
= 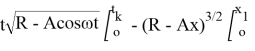 =
=
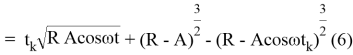
Подставив полученное значение интеграла в (5), получим:
![]()
![]()
![]() (7)
(7)
Полная площадь хлопковой обмотки равна:
![]() (8)
(8)
Тогда полнота съема равна
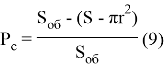
или
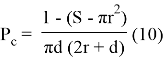
Если при повороте шпинделя на угол π расстояние ОшОс — r > d, то необходимо решить уравнение:
ОшОс — r с = r + d (11)
или
![]() (12)
(12)
Решив это уравнение методом приближение, определим t1 и подставляя в (7), вычислим часть необработанной площадки по формуле
![]() (13)
(13)
Другая часть необработанной площадки определяется по формуле
![]() (14)
(14)
или
![]() (15)
(15)
Тогда полнота съема равна
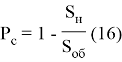
Как видно из (16), полнота съема хлопка зависит от R1, r, ω, rc, d.
При применение второго съемника полнота съема увеличивается, необработанную площадь определим из (7), подставляя t=π/2. При этом полнота съема равна
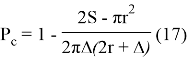
Необходимо отметить, что необработанная площадь при использовании второго съемника зависит от взаимного их расположения. При этом угол расположения съемников должен обеспечить подход ко второму съемнику необработанной первым съемников полнота съема определяется по (17). Полнота съема хлопка в зависимости от взаимного расположения съемников — θ (центральный угол барабана) показана на рис.2.
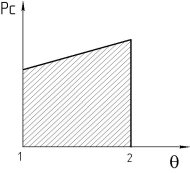
Рис. 2. Влияние угла θ на полноту съема
В зоне съема хлопкоуборочного аппарата происходит самосброс хлопка со шпинделей [1], количество которого зависит от угловой скорости шпинделя. Исследований показали, что при угловой скорости шпинделя ω=100–120 рад/с самосброс хлопка составляет 30–40 % от всего хлопка, а при 200–250 рад/с — 90–100 %. Поэтому можно в первом приближении предположить, что вероятность самосброса хлопка со шпинделей равна:
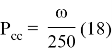
Тогда полноту съема с учетом самосброса находим как
![]()
Для обеспечения максимума частоты вращения шпинделя и надежности работы радиус ролика шпинделя обычно принимают минимально возможным, т. е. 11,5–12,5 мм. С учетов второго получим взаимосвязь угловых скоростей шпинделя и барабана, т. е.
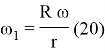
Расчеты показали взаимосвязь полноты съема хлопка с радиусом шпиндельного барабана: для шпинделей диаметрами 24 и 30 мм с увеличением диаметра шпиндельного барабана улучшается полнота съема до 140 мм интенсивно, а далее умеренно. По расчетам для серийного аппарата вероятность полноты съема равна 0,9–0,98 для первой, 0,8–0,86 для второй пары барабанов.
Литература:
- Шполянский Д. М. Технологические основы параметров рабочих органов и схемы хлопкоуборочных машин, Ташкент,: Мехнат, 1985
- А. Д. Глущенко, М. Т. Ташболтаев. Динамика узлов вращения уборочных аппаратов хлопкоуборочных машин.., Ташкент, Фан, 1990

