Об управлении положением центра масс подводного робототехнического понтона с якорно-тросовыми движителями



Рассматривается задача влияния положения центра масс на усилия в тросах, управление длиной которых обеспечивает поступательное движение перемещаемого объекта в плотных средах.

Ключевые слова: движитель, мобильный робот.

The problem of the influence of the position of the center of mass on the forces in the cables, the control of the length of which ensures the translational motion of the object being moved in dense media.

Keywords: propulsive device, mobile robot.

Введение

Среди робототехнических систем предназначенных для перемещения по дну водоемов известны роботы, выполненные на основе понтонов, перемещающихся с помощью якорно-тросовых движителей [1,2]. Кинематическая схема и принцип работы таких движителей представлены на рис. 1.

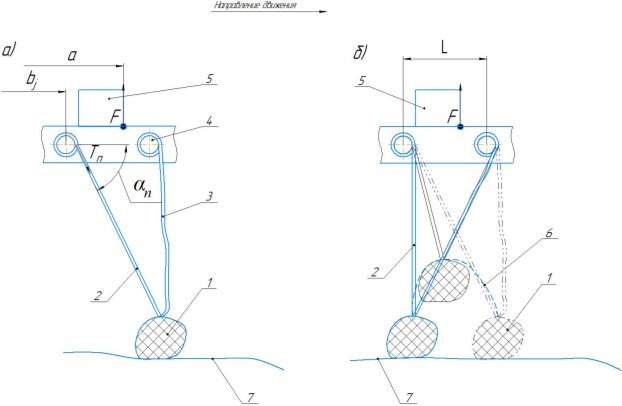
Рис. 1. Кинематическая схема и принцип работы якорно-тросового движителя мобильного робота с положительной плавучестью: а), б) — соответственно исходное и последующее положение фрагмента робота 1 — якорь, 2, 3 — тросы, 4 — управляемые барабаны, 5 — передвижной груз для изменения положения центра масс,6 — траектория переноса якоря, 7 — профиль дна, a — расстояние от центра масс робота до точки приложения выталкивающей силы F, b_j — расстояние от центра масс робота до оси барабана, α_{n —} угол ориентации троса

Одной из особенностей таких движителей, в силу работы тросов на растяжение, является существование перераспределения сил натяжения при передвижении понтонов с сохранением их ориентации и, тем более, при переносе, как минимум одного движителя в новое положение. В отличии от известных шагающих машин [3, 4] где также при движении изменяются силы взаимодействия с грунтом, за счет его деформации, у якорно-тросовых движителей следует управлять приводами для обеспечения необходимых сил натяжения, обеспечивающих требуемую ориентацию понтона.

Постановка задачи

Одной из проблем передвижения роботов с помощью движителей, дискретно взаимодействующих с опорной поверхностью, является проблема энергетической эффективности [6, 7, 8]. Известны различные способы ее решения, и в частности за счет выбора программного движения робототехнического средства, обеспечивающего минимум энергетических потерь [9, 10]. Минимум энергетических потерь можно обеспечить за счет управления усилиями в тросах, а их величину I определить выражением [6].

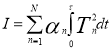(1)

где T_n — сила натяжения n троса, N — количество двигателей, α_n- известный параметр двигателя, τ- время, за которое удобно измерить время перемещения понтона на расстояние L со скоростью v₀.

τ = L/v (2)

Предположим, что все двигатели одинаковы, тогда α_n в (1) можно опустить. Усилия T_n зависят от многих факторов: количества движителей, рельефа дна, скорости движения, положения центра масс и центра давления.

В работе рассматривается поступательное движение, с прямолинейным движением центра масс, перемещение робота-понтона, на котором установлено дополнительное тело, которое может вызывать изменение положение центра масс (a) понтона, что влияет на усилия T_n.

Ставится задача найти закон изменения положения центра масс a=a(t), обеспечивающего минимум энергетических потерь (1) при движении с заданной скоростью v и при неизменных остальных параметрах.

Метод решения

Уравнения равновесия перемещаемого объекта с учетом квазистатического характера поступательного движения представлены в виде системы из трех уравнений, линейных относительно сил T_i натяжения тросов:

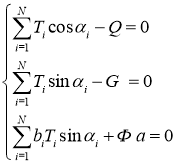(3)

В данном случае, при N ≥ 3, задача является статически неопределимой. При трех натянутых тросах исследуемая задача равновесия объекта становится статически определимой, систему уравнений (3) можно записать в виде (4), в случаях не общих, где количество неизвестных больше 3, а задача становится статически неопределимой, применяются дополнительные уравнения [10]:

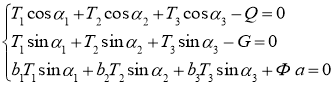,(4)

решение, которой относительно T₁, T₂, T₃ тривиально.

Полученная система линейных уравнений позволяет определить усилия в тросах в зависимости от положения объекта.

Таблица 1

Значения параметров моделируемой системы

Параметр	Значение
b1, м	15
b2, м	4
b3, м	-8
G, кН	400
Ф, кН	500
L, м	3
h1, м	5
h2, м	5
h3, м	5
l1, м	3
l2, м	0
l3, м	2

Результаты расчетов

Рассмотрим три варианта системы при постоянной силе сопротивления Q = 50 кН, но с изменением параметра а, рассмотрены будут варианты с размером 1, 2 и 2,5 метра. Результаты расчетов при решении с учетом размера а=1 представлены в таблице 2.

Таблица 2

Результаты расчета сил натяжения при а=1

dS	0	0,1	0,2	0,3	0,4	0,5
T1	64341,54	60954,19	47928,82	35127,74	22542,4	1078,1
T2	2586,207	8407,474	32299,86	55791,12	78898,42	100510,8
T3	45495,36	42790,65	31884,79	21124,39	10499,52	522,1592
Тср	37474,37	37384,1	37371,16	37347,75	37313,45	34037,02

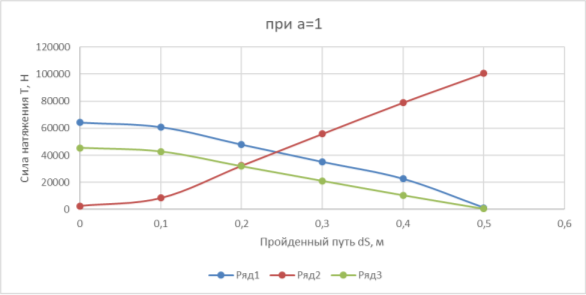
Рис. 2. График зависимости сил натяжения T от пройденного пути dS при а=1

На рисунке 2 показан график зависимости силы натяжения тросов в зависимости от перемещения платформы, как видно из рисунка 1 перед достижением значения 0,1 происходит перенос якоря и изменение характеристик происходит скачкообразно сила натяжения второго троса начинает расти, а двух остальных начинает уменьшаться.

Далее рассмотрим результаты с а=2, результаты расчетов показаны в таблице 3, а график зависимости на рисунке 3.

Таблица 3

Результаты расчета сил натяжения при а=2

dS	0	0,1	0,2	0,27	0,3	0,4	0,5
T1	84448,27	86104,13	87737,76	88869,22	86786,19	73775,14	61618,17
T2	11206,9	7242,827	3278,482	500,7285	4132,676	27665,68	49670,75
T3	17641,06	19550,9	21439,77	22750,58	21124,39	10499,52	522,1592
Тср	37765,41	37632,62	37485,34	37373,51	37347,75	37313,45	37270,35973

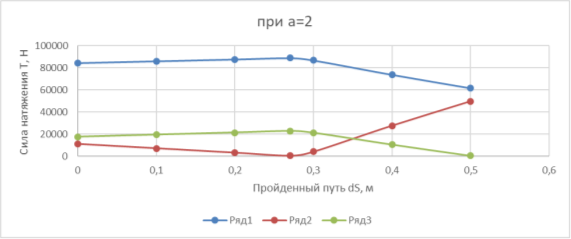
Рис. 3. График зависимости сил натяжения T от пройденного пути dS при а=2

При изменении параметра а мы видим прирост пройденного пути dS на 0,1 метра, а значения сил натяжения выросли примерно на 30 %.

Далее рассмотрим случай, когда а=2,5, результаты расчета представлены в таблице 4, а график зависимости представлен на рисунке 4.

Таблица 4

Результаты расчета сил натяжения при а=2,5

dS	0	0,1	0,2	0,3	0,4
T1	94501	96069,89	97618,14	99148,59	100512,6
T2	15517,24	11554,03	7592,273	3627,201	51,88124
T3	3713,907	5717,717	7696,329	9651,663	11393,18
Тср	37910,72	37780,55	37635,58	37475,82	37319,22

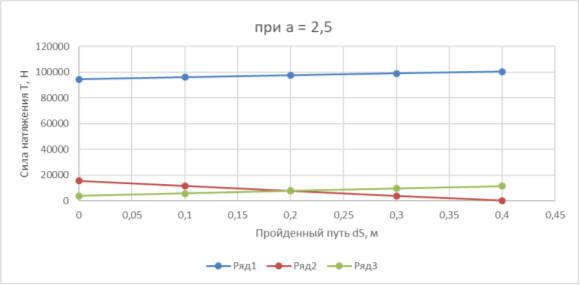
Рис. 4. График зависимости сил натяжения T от пройденного пути dS при а=2,5

Анализируя рисунок 4 и результаты расчета из таблицы 4 можно сделать вывод, что пройденное расстояние составляет те же, что и в первом случае 0,4 метра, однако значения сил натяжения по сравнению с первым случаем увеличиваются более чем на 50 %, а кривая графика приобретает практически линейный вид.

Далее рассмотрим параметр оптимизации I, формула для его расчета представлена ниже:

(5)

А результат представлен в таблице 5.

Таблица 5

Результат расчета параметра Iв зависимости от dS

dS	0	0,1	0,2	0,3	0,4	0,5
I1	2003365022	1424424780	167282524,1	608283751	2666480490	6628299729
I2	3289633334	3599975398	3952875167	3810597900	2141521146	2097015786
I3	4873349756	5113502769	5396866550	5723443280	6054417364

Также зависимость представлена на рисунке 5:

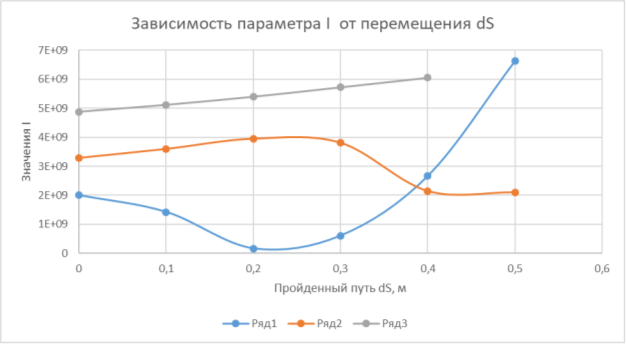
Рис. 5. График зависимости параметра I от перемещения dS.

Как видно из представленных результатов в первом случае изменяется очень круто и после переноса одного якоря происходит неприемлемое увеличение параметра I, в третьем случае график практически линейный, но значения очень большие, поэтому наиболее приемлемым для дальнейшего исследования можно принять второй случай.

Анализ результатов

Анализ полученных результатов показывает:

 Пройденный путь dS почти не изменяется;

 Пиковые значения сил натяжения Т возрастают при увеличении расстояния между центром масс и центром плавучести платформы;

 Наиболее оптимальным значением по параметру I, является второй вариант расчета среди рассмотренных со значением размера а=2.

Из произведенной работы видно, что перемещение якоря 2 происходит при достижении значения силы натяжения в тросе равном нулю, затем наблюдается достижение угла в 270 градусов другими якорями и падение силы натяжения в их тросах, а в движителе 2, где произошел перенос якоря, происходит рост силы натяжения, тогда как в остальных движителях значение этой силы снижается.

Литература:

1. Об оценке эффективности цикловых механизмов / Брискин Е. С., Калинин Я. В., Малолетов А. В. / Известия Российской академии наук. Механика твердого тела. 2017. № 2. С. 13–19.
2. О принципах движения роботизированных систем с движителями якорно-тросового типа / Пеньшин И. С., Смирная Л. Д., Брискин Е. С./ В книге: Прогресс транспортных средств и систем — 2018 Материалы международной научно-практической конференции. Под редакцией И. А. Каляева, Ф. Л. Черноусько, В. М. Приходько. 2018. С. 163.
3. Mathematical modelling of mobile robot motion with propulsion device of discrete interacting with the support surface / Briskin E. S., Kalinin Y. V., Maloletov A. V.,Sharonov N. G. / IFAC-PapersOnLine (см. в книгах). 2018. Т. 51. № 2. С. 236–241.
4. Шагающая опора для транспортных средств повышенной проходимости / Охоцимский Д. Е., Брискин Е. С., Чернышев В. В., Шерстобитов С. В. / патент на изобретение RUS 2156711 09.06.1999
5. Об управлении движением автономного робототехнического комплекса с якорно-тросовым движителем / Платонов В. Н., Брискин Е. С., Шаронов Н. Г. / В книге: Прогресс транспортных средств и систем — 2018 Материалы международной научно-практической конференции. Под редакцией И. А. Каляева, Ф. Л. Черноусько, В. М. Приходько. 2018. С. 146–148.
6. Оптимизация в инженерных и управленческих задачах / Волчков В. М., Годенко А. Е., Калинин Я. В., Тарасова И. А. / Учеб. пособие / Волгоград, 2018.
7. Математическое моделирование робота с переменным вектором тяги / Павловский В. Е., Яцун С. Ф., Емельянова О. В., Стуканёва С. П. / В сборнике: Второй Всероссийский научно-практический семинар «Беспилотные транспортные средства с элементами искусственного интеллекта» Труды семинара. Российская ассоциация искусственного интеллекта. 2015. С. 99–106.
8. Walking robot «character» as element of intelligent system / Briskin E. S., Maloletov A. V., Sharonov N. G., Kalinin Ya. V., Leonard A. V., Serov V. A., Shurygin V. A. / В сборнике: Advances in Cooperative Robotics: Proceedings of the 19th International Conference on Climbing and Walking Robots and the Support Technologies for Mobile Machines, CLAWAR 2016 19th. 2016. С. 386–394.
9. Об особенностях управления движением мобильных роботов с движителями якорно-тросового типа / Брискин Е. С., Серов В. А., Шаронов Н. Г., Пеньшин И. С. / Экстремальная робототехника. 2017. № 1. С. 336–343.