На траекторию движения плавающих машин влияют многие факторы, такие как скорость ветра, размер машины, глубина реки и, что наиболее важно, скорость течения и т. д., в объеме статьи показано только влияние скорости течения на траекторию плавающих машин.
Ключевые слова: плавающие машины, влияние, течения, траектория, управляемость.
- Выбор системы координаты.
Для описания движения машины вводят две системы координат — неподвижную Х0ОУ0, и подвижную ХGУ, жестко связанную с машиной. Направление осей неподвижной системы координат выбирается таким образом, чтобы в начальный момент она совпадала с подвижной как показано на рис.1.
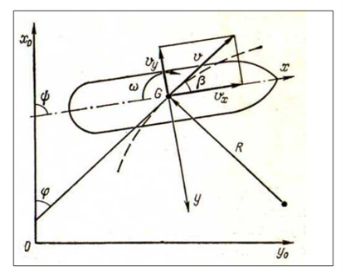
Рис. 1. Схема исследования траектории плаваюших машин при повороте
Угол Ψ, образуемый с диаметральной плоскостью (ДП) и осью Х0, называется углом курса.
Угол курса может быть выражен через другие углы, а именно через:
− центральный угол дрейфа, измеряемый между мгновенным вектором скорости центра тяжести (ЦТ) машины и диаметральной плоскостью β;
− угол траектории или угол скорости φ, измеряемый между вектором скорости и осью Х0.
- Построение траектории плавающих машин.
Для оценки влияния течения на управляемость плавающих машин мы построим траектории движения машины в двух случаях: при течении и без течения с тестовым исходным данным.
Движение машин может быть задано проекциями скорости центра тяжести (ЦТ) на подвижные оси и угловой скоростью. Однако во многих случаях более удобной оказывается другая система кинематических параметров — модуль скорости ЦТ машин │V│, угол дрейфа β, и угловая скорость Ω.
Координаты машины в неподвижной системе координат определяются следующими соотношениями:
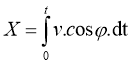 (1.1)
(1.1)
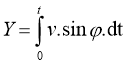 (1.2)
(1.2)
Где:
v — абсолютная скорость движения машин относительно системы координаты Х0ОУ0.
![]() : угол траектории или угол скорости φ, измеряемый между вектором скорости и осью Х0.
: угол траектории или угол скорости φ, измеряемый между вектором скорости и осью Х0.
При этом траектория машин без течения (скорость течения равно нулю) определяется следующем образом:
По оси OX:
X=![]()
По оси OY:
Y= ![]()
При существовании течения абсолютная скорость vи относительно системму координаты Х0ОУ0 определяется как показано на рис.2.
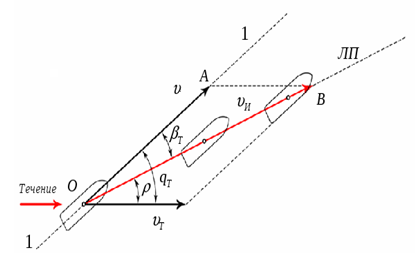
Рис. 2 Влияние течения на абсолютную скорость плавания машин
Траектория машин при существовании течения определяется следующем образом:
По оси OX:
X= ![]()
По оси OY:
Y= ![]()
Расчетные тестовые исходные данные для плавающего танка ПТ -76
|
№ |
Параметры |
Обозначение |
Единица |
Величина |
|
1 |
Вес машины |
G |
Т |
14.0 |
|
2 |
Длина мащины |
L |
м |
5.75 |
|
3 |
Ширина машины |
B |
м |
2.35 |
|
4 |
Высота машины |
H |
м |
1.945 |
|
5 |
Скрость плавания |
v |
м/c |
2,8 |
|
6 |
Угол дрейфа |
β |
Рад. |
0.52 |
|
7 |
Скорость течения v1 |
v1 |
v/c |
1,4 |
|
8 |
Скорость течения v2 |
v2 |
v/c |
1,8 |
|
9 |
Угол скорости |
φ |
Рад |
0,78 |
|
10 |
Относителный радиус поворот |
R |
м |
10 |
|
11 |
Угловая скорост |
ω |
Рад/с |
0,28 |
Результаты расчетной оценки влияния скорости течения на траекторию плавания машин путем использования программы MathLap.
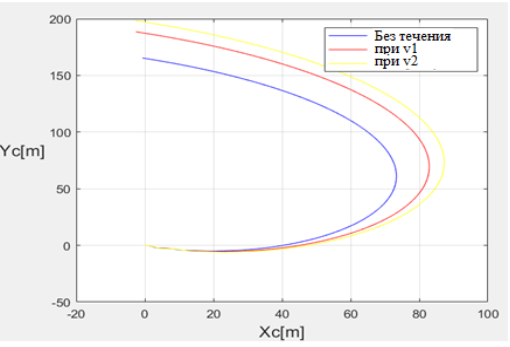
Рис. 3. Траектория плавающего танка при разных режимах скорости течения
3. Обсуждения:
На рис 3 показана траектория плавющего танка ПТ-76 в трех случаях: при отсутствии течения, при скорости течения v1 = 1,4 и v2 = 1,8 м/с. Видно, что на траекторию плавающих машин при повороте влияет скорость течения. Тем больше скорость течения, чем траектория более отклоняется. Зная об этом, механик водитель должен управлять машиной разумно в различных ситуациях.
Литература:
- Đinh Văn Kiên (2015), Đánh giá khả năng bơi của xe PT-76 sau khi lắp phao tăng độ nổi dự trữ, Luận Văn Thạc sỹ kỹ thuật, HVKTQS.
- The Mathwork Inc “SIMULINK Dynamic system simulation for MATLAB” (2000), http://www.mathworks.com.
- А. П. Стелaнов, (1983), Koнcmpyupoвaнue u pacчem nлaвaюшux мaшuн, Mocквa.







