Моделирование двумерных и пространственных течений в местных сопротивлениях пневмогидросистем высокоэнергетических силовых установок



С использований программ CFD проведен расчет двумерных и пространственных течений в местных сопротивлениях высокоэнергетических двигательных установок, проведено сравнение с известными эмпирическими моделями и экспериментальными данными.

Ключевые слова: пневмогидросистемы, трубопроводы, местное сопротивление, двухпозиционный дроссельный клапан, уравнения Навье — Стокса, модели турбулентности.

Разработка и создание новых высокоэнергетических установок сопровождается проведением большого количества гидравлических и газодинамических расчетов [1–3], и является наукоемким итерационным процессом, включающим большое количество модельных и натурных экспериментов. Использование компьютерного моделирования высокоэнергетических силовых установок [3] позволяет сократить время принятия решений при реализации проектов, уменьшить время экспериментальной отработки, повысить конкурентоспособность разрабатываемых новых высокоэнергетических силовых установок.

Отработка пневмогидросистем ЖРД обычно связана с необходимостью проведения испытаний для определения гидравлических потерь, как во всей системе в целом, так и в отдельных ее элементах. В связи с этим актуальной становится оценка гидравлических сопротивлений при помощи численного моделирования. В данной работе рассмотрена задача моделирования течений в местных сопротивлениях и в дроссельном клапане горючего, располагающегося в магистрали подачи компонента в газогенератор. Проведено сравнение результатов расчета с аналитическими методиками и результатами эксперимента.

Одной из проблем, возникающих при глубоком дросселировании тяги ЖРД, является возникновение низкочастотной неустойчивости в магистралях, уменьшить вероятность появления, которой можно путём перераспределения гидравлических потерь. Для этого используют местные сопротивления и специальные гидравлические сопротивления, в данном случае — двухпозиционный дроссельный клапан. Пневмогидравлическая схема двигательной установки представлена на рис. 1.

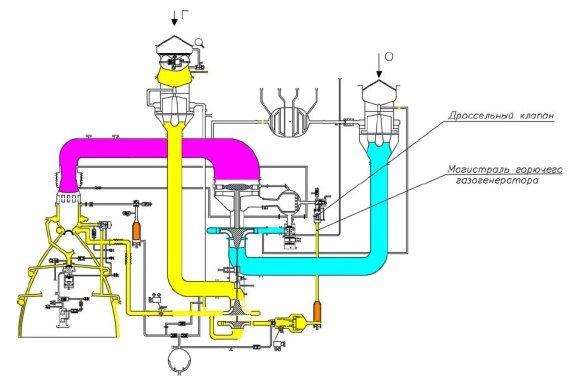
Рис. 1. Пневмогидросистема двигательной установки

Современные пакеты CFD позволяют решать двумерные и пространственные задачи прикладной гидрогазодинамики в стационарной и нестационарной постановках в широком диапазоне скоростей и давлений потока. Течение рабочего тела может рассматриваться как невязкое, ламинарное или турбулентное. Моделирование турбулентных течений в местных сопротивлениях и дроссельном клапане проводилось с помощью уравнений Рейнольдса (RANS), замкнутых при помощи различных моделей турбулентности.

Для выбора предпочтительной модели турбулентности и характерных размеров сетки был проведен расчет турбулентного течения потока жидкости в местных сопротивлениях: во внезапном сужении и внезапном расширении. Качественная картина течения во внезапном сужении из [4] и линии тока, полученные в результате расчета, представлены на рис. 2.

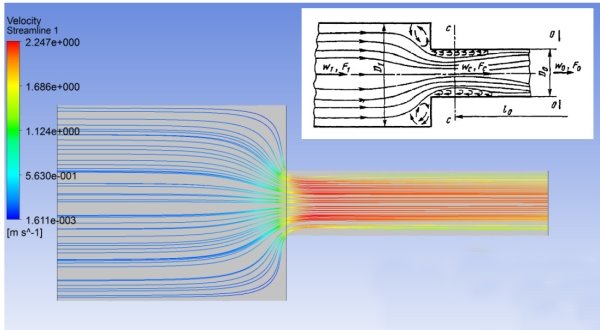
Рис. 2. Течение во внезапном сужении

Качественная картина течения во внезапном расширении из [4] и распределение скоростей, полученных в результате расчета, представлены на рис. 3.

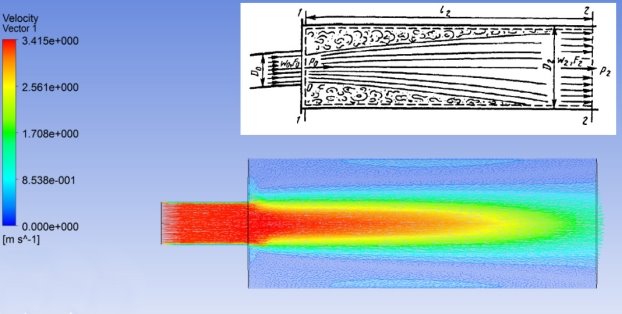
Рис. 3. Течение во внезапном расширении

Для сравнения различных моделей турбулентности было рассмотрено течение в канале с внезапным сужением со следующими характерными размерами: D₁=48 мм и D₀=24 мм (рис. 4). Скорость потока на входе составляла 3 м/с, давление потока на выходе равнялось 1 атм. Сетка строилась ортогональная, со сгущением ячеек к горизонтальным и вертикальным стенкам. Общее количество ячеек сетки составляло около 30000. Рассматривались модели турбулентности Спаларта-Аллмареса (SA), k — ε, k — ω, SST.

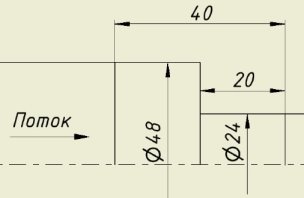
Рис. 4. Геометрия канала с внезапным сужением

Сравнение результатов моделирования течения проводилось с потерями давления в местном сужении, определенными по методике [4].

Потери давления в местном сопротивлении определяются по формуле

,

где ζ — коэффициент сопротивления, ρ — плотность среды, w_{0 —} скорость среды до сужения.

ζ = 0,5·a + ζ_тр, где

a = f₁(F₀/F₁), ζ_тр — коэффициент сопротивления трения.

a = f₁(F₀/F₁) = f₁(0,25) =0,8.

Δp_вс=29164 Па.

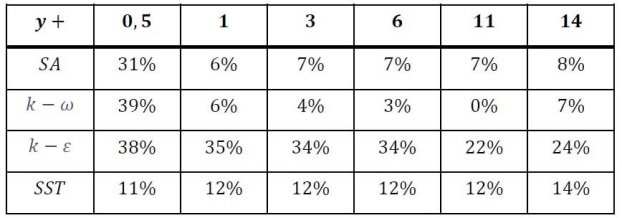
Результаты расчета турбулентного течения во внезапном сужении при различных моделях турбулентности представлены на рис. 5 и в таблице 1.

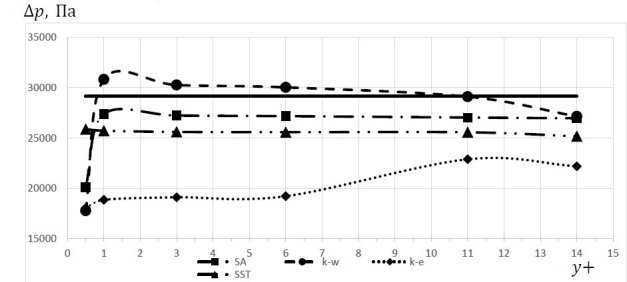
Рис. 5. Зависимость перепада давления во внезапном сужении от пристеночного параметра y+ для различных моделей турбулентности

Таблица 1

Результаты расчета течения во внезапном сужении

Геометрия канала с внезапным расширением приведена на рис. 6.

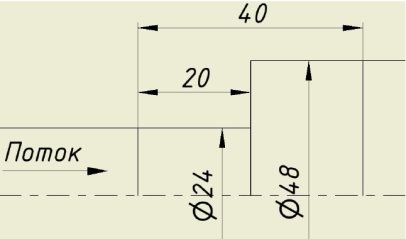
Рис. 6. Геометрия канала с внезапным расширением

Рассчитанное значение перепада давления по методике [4] в канале с внезапным расширением составляет Δp_вр=2657 Па.

Моделирование турбулентного течения на входе проводилось при следующих начальных данных: жидкость — вода; скорость потока на входе — 3 м/с. Давление в выходном сечении — 1 атм. Количество ячеек сетки около 32000. Результаты расчета турбулентного течения во внезапном расширении при различных моделях турбулентности представлены на рис. 7 и в таблице 2.

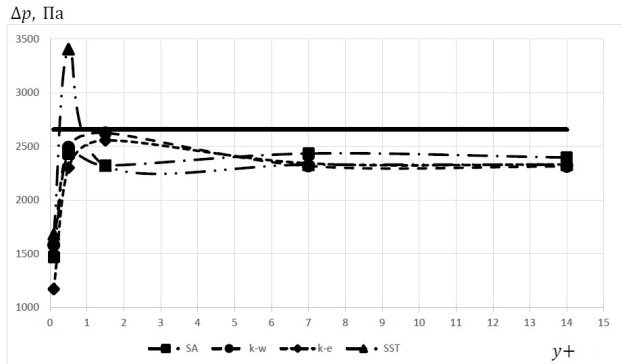
Рис. 7. Зависимость перепада давления во внезапном расширении от пристеночного параметра y+ для различных моделей турбулентности

Таблица 2

Результаты расчета течения во внезапном расширении

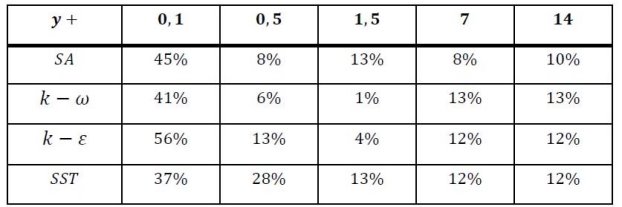
Как видно из приведенных результатов, модель турбулентности SST обладает наименьшей чувствительностью к изменению параметра y+. Эта модель и модель SA использовались при дальнейшем анализе течений в дроссельном клапане.

Для обеспечения ступенчатого изменения сопротивления в магистрали используется дроссельный клапан, имеющий два рабочих положения, рассчитанных на номинальный режим и режим глубокого дросселирования. В нормальном положении клапан открыт, по команде подаётся управляющее давление и клапан переходит на режим глубокого дросселирования. Внешний вид двухпозиционного дроссельного клапана представлен на рис. 8.

Рис. 8. Дроссельный клапан

Дроссельный клапан при открытом положении регулирующего элемента показан на рис. 9. При открытом положении клапана поток жидкости проходит как через центральное отверстие, так и боковые отверстия дросселирующего элемента.

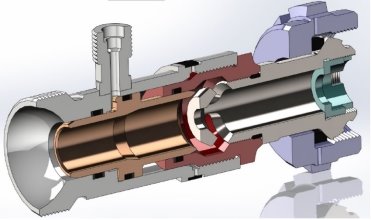
Рис. 9. Дроссельный клапан в открытом положении

При работе клапана в режиме глубокого дросселирования (рис. 10) поток жидкости проходит только через центральное отверстие дросселирующего элемента.

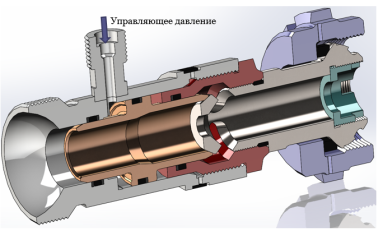
Рис. 10. Дроссельный клапан в закрытом положении

Сетка расчетной области открытого клапана приведена на рис. 11.

Рис. 11. Сетка проточной части дроссельного клапана в открытом положении

Сетка проточной части закрытого дроссельного клапана показана на рис. 12.

Рис. 12. Сетка проточной части дроссельного клапана в закрытом положении регулирующего элемента

Проведен двумерный и пространственный расчет течений в дроссельном клапане при открытом и закрытом положении регулирующего элемента с использованием пакетов ANSYS Fluent и Flow Simulation. Картина линий тока представлена на рис. 13 и рис. 14. При открытом дроссельном клапане линии тока проходят через центральное и боковые отверстия и образуют жгут в центральной части канала. Структура потока существенно несимметрична (рис. 13).

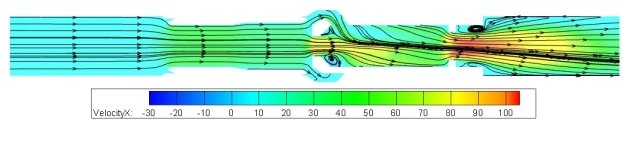
Рис. 13. Структура течения в открытом дроссельном клапане

При течении в закрытом клапане структура потока обладает большей симметрией и представляет собой комбинацию течений во внезапных расширениях и местном сужении (рис. 14).

Рис. 14. Структура течения в закрытом дросселе

Расчет дроссельного клапана проводился при следующих граничных условиях.

А. Открытое положение регулирующего элемента:

расход жидкости — 8,9 кг/c; ν_Т/ν=100; давление потока на выходе из клапана 13,95 МПа; число расчетных ячеек — 850000.

Б. Закрытое положение регулирующего элемента:

расход жидкости — 1,36 кг/c; ν_Т/ν=100; давление потока на выходе из клапана 18,4 МПа; число расчетных ячеек — 940000.

Результаты расчетов и сравнение с экспериментальными данными представлены в таблице 3.

Таблица 3

Сравнение расчетных иэкспериментальных данных

Положение дросселя	Расход воды, кг/c	Δp, атм, эксперимент (среднее)	Δp, атм, Fluent (SST)	Δp, атм, Fluent (SA)	Δp, атм, Flow Simulation
открытое	8,9	49,74	80,2	75,5	60,3
закрытое	1,36	6,9	5,95	6,37	6,9

Из сравнения результатов видно, что расчетная модель дает хорошее совпадение с экспериментом при закрытом положении регулирующего элемента дроссельного клапана. При открытом положении регулирующего элемента дроссельного клапана течение в проточной части дросселя становится существенно трехмерным и для получения более точных решений требуется построение сетки с большим числом элементов, адаптированных к особенностям течения. В частности, для анализа нестационарного течения в газовом клапане SSME была построена сетка, содержащая 55 млн ячеек.

Выводы:

1) проведен анализ влияния модели турбулентности и размера сетки на результаты моделирования течений потока жидкости в местных сопротивлениях;

2) выбраны предпочтительные модели турбулентности и размеры сетки для данного класса задач;

3) проведен сравнительный анализ экспериментальных данных и результатов численного моделирования течения в проточной части двухпозиционного дроссельного клапана;

4) выявлена потребность в большей размерности сетки, а также больших вычислительных мощностях.

Литература:

1. Основы теории и расчёта жидкостных и ракетных двигателей / А. П. Васильев, В. М. Кудрявцев, В. А. Кузнецов, В. Д. Курпатенков. А. М. Обельницкий, В. М. Поляев, Б. Я. Полуян. — Изд. 2-е, перераб, и доп. — М.: Высшая школа, 1975. — 656 с.
2. Прикладная газовая динамика / Б. И. Каторгин, А. С. Киселев, Л. Е. Стернин, В. К. Чванов. — М.: Вузовская книга, 2014. — 340 с.
3. Математическое моделирование рабочего процесса жидкостных ракетных двигателей / Е. Н. Беляев, В. К. Чванов, В. В. Черваков. — М.: Изд-во МАИ, 1999. — 228 с.
4. Идельчик И. Е. Справочник по гидравлическим сопротивлениям / Под ред. М. О. Штейнберга. — 3-е изд. — М.: Машиностроение, 1992. — 672 с.
5. ANSYS FLUENT 19.0 Documentation. Ansys Inc., 2018.