В данной статье оцениваются модели прогнозирования спроса на наборе из 3 классов продуктов (SKU) через 3 последовательных периода продолжительностью 28 дней.
Оценивались следующие модели:
− экспоненциальное сглаживание
− ARIMA
− модель Prophet
Используются в основном два показателя точности прогнозирования: среднеквадратическая ошибка и средняя абсолютная процентная ошибка.
Сначала стоит обсудить результаты прогнозирования спроса на каждый класс продукции по отдельности. Начнем с первого (SKU1).
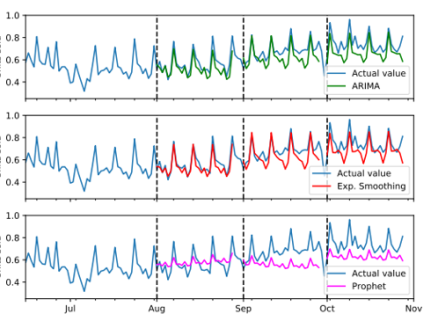
Рис. 1. Результаты оценки прогнозирования первого класса продуктов — SKU1
Таблица 1
Результаты прогнозирования SKU1
|
Эксп. сглаживание |
ARIMA |
Prophet | ||||
|
MAPE |
RMSE |
MAPE |
RMSE |
MAPE |
RMSE | |
|
Период 1 |
5.918 |
0.042 |
8.536 |
0.062 |
10.907 |
0.077 |
|
Период 2 |
9.459 |
0.079 |
10.176 |
0.083 |
17.506 |
0.139 |
|
Период 3 |
9.327 |
0.087 |
10.917 |
0.095 |
14.426 |
0.129 |
Как из рисунка, так и из таблицы видно, что наилучшими моделями были модели ARIMA и экспоненциального сглаживания, которые дают довольно похожие прогнозы, однако метод сглаживания имеет несколько лучшие результаты. Обе модели хорошо адаптированы к недельной сезонности в прогнозе первого периода, немного меньше в других периодах, возможно, потому, что они чрезмерно приспособлены к модели сезонности, которая немного изменилась в более поздние периоды тестирования. Обе модели недооценили наклон тренда во втором и третьем периоде, а именно модель сглаживания во втором периоде, скорее всего потому, что она выбрала достаточно низкий параметр тренда β = 0.06. Прогнозы модели Prophet, похоже, также адаптированы к сезонности, но несколько затухают. Во втором периоде модель Prophet предсказывала тенденцию к снижению, в то время как на самом деле она увеличивалась, что привело к худшему результату.
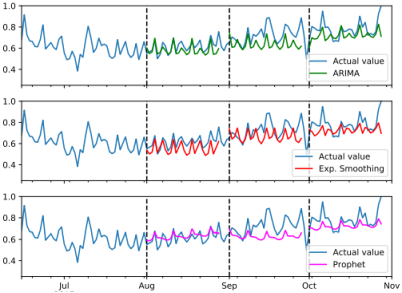
Рис. 2. Результаты оценки прогнозирования первого класса продуктов — SKU2
Таблица 2
Результаты прогнозирования SKU2
|
Эксп. сглаживание |
ARIMA |
Prophet | ||||
|
MAPE |
RMSE |
MAPE |
RMSE |
MAPE |
RMSE | |
|
Период 1 |
10.072 |
0.076 |
7.227 |
0.060 |
6.954 |
0.052 |
|
Период 2 |
10.744 |
0.112 |
13.106 |
0.133 |
12.630 |
0.126 |
|
Период 3 |
8.532 |
0.094 |
8.662 |
0.091 |
8.129 |
0.087 |
Для всех периодов была выбрана модель ARIMA порядка (1, 1, 2)x(1, 1, 1)7, которая хорошо работала в первом и третьем периодах тестирования. Параметры метода экспоненциального сглаживания выбирались всегда немного по-разному для каждого периода. Для первого периода было α ∼ 0.01, β ∼ 0.95, φ ∼ 0.95, γr ∼ 0.04 и γw ∼ 0.34, для второго α ∼ 0.11, β ∼ 0.49, φ ∼ 0.92, γr ∼ 0.04 и γw ∼ 0.42, а третий α ∼ 0.17, β ∼ 0.74, φ ∼ 0.92, γr ∼ 0.04 и γw ∼ 0.26, поэтому тенденция и недельный сезонность параметров поменялся, но это всегда приводило к хорошим оценкам. В среднем модель Prophet давала наиболее точные прогнозы с небольшим отрывом.
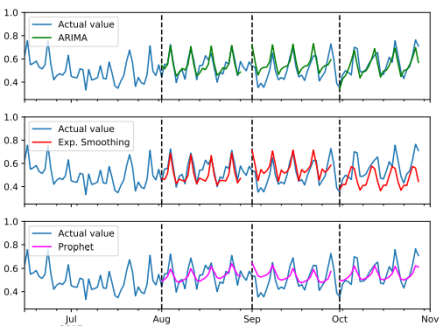
Рис. 3. Результаты оценки прогнозирования первого класса продуктов — SKU3
Таблица 3
Результаты прогнозирования SKU3
|
Эксп. сглаживание |
ARIMA |
Prophet | ||||
|
MAPE |
RMSE |
MAPE |
RMSE |
MAPE |
RMSE | |
|
Период 1 |
9.438 |
0.067 |
7.677 |
0.051 |
10.245 |
0.066 |
|
Период 2 |
15.991 |
0.088 |
16.248 |
0.087 |
15.372 |
0.089 |
|
Период 3 |
17.712 |
0.127 |
8.320 |
0.06 |
9.686 |
0.071 |
Закончим оценку каждого продукта с классом продукта 3 (SKU3). SKU3 — это класс, состоящий из популярных напитков, что может быть причиной того, что исторические данные показывают повторяющуюся еженедельную сезонность. В первый период тестирования все модели, похоже, хорошо вписываются в сезонность. Однако во втором тестовом периоде разница между минимумами и максимумами серии выросла, и в начале сентября наблюдается небольшое падение уровня (возможно, потому, что в это время заканчиваются летние каникулы). Ни одна из моделей этого не предсказывала.
Возможно, некоторые классы продуктов потребуют моделей, скорректированных для этих «праздничных» эффектов. Для SKU3, модели ARIMA заказов (1, 1, 2)x(1, 1, 1)7, (1, 1, 1)x(1, 1, 1)7, (1, 1, 2)x(0, 1, 1)7 были выбраны для каждого периода соответственно. Модель ARIMA (1, 1, 1)x(1, 1, 1)7, выбранная для второго периода, имела самый высокий MAPE из них, возможно, было бы лучше, если бы процесс выбора модели выбрал ту же модель для всех периодов. Метод экспоненциального сглаживания дает аналогичные результаты для обеих ARIMA в первые два периода. Но параметры α ∼ 0.32, β ∼ 0.08, φ ∼ 0.95, γr ∼ 0.54 и γw ∼ 0.04, выбранные для третьего периода, привели к MAPE 17.7 %. Параметры показывают признаки чрезмерной подгонки, так как компонент уровня довольно высок, а компонент тренда низок.
Теперь рассмотрим остатки предлагаемых методов прогнозирования, поскольку мы хотим генерировать сценарии спроса для кадастровых моделей, используя распределение, оцененное по среднему значению выборки и дисперсии выборки остатков.
Для оценки возможных автокорреляций остатков можно использовать график автокорреляции. Пример графика автокорреляции можно увидеть на рисунке 4 который был создан из остатков ARIMA и моделей экспоненциального сглаживания, выбранных для прогнозирования спроса в первом периоде тестирования для SKU1. На графике видно, что остатки модели экспоненциального сглаживания значительно коррелируют, в то время как остатки модели ARIMA практически не коррелируют.
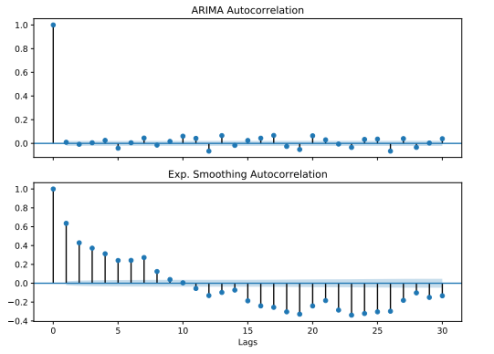
Рис. 4. Автокорреляционные графики остатков моделей ARIMA и экспоненциального сглаживания
Другим вариантом обнаружения автокорреляции является тест Люнг-Бокса.
Таблица 4
Тест Люнг-Бокса
|
SKU1 |
SKU2 |
SKU3 | |
|
ARIMA |
0.15 |
0.32 |
0.28 |
|
Smoothing |
~ 0 |
~ 0 |
~ 0 |
В таблице 4 приведены p-значения статистики теста Люнг-Бокса для первых 14 лагов, рассчитанные на основе остатков моделей, выбранных для прогнозирования спроса в первом периоде тестирования для всех SKU. Согласно таблице, можно отклонить гипотезу о том, что остатки экспоненциальных моделей сглаживания независимы. Относительно высокие p-значения модели ARIMA предполагают, что мы не можем отвергнуть гипотезу о том, что ее остатки независимы.
Таблица 5
Тест Шапиро-Уилка
|
SKU1 |
SKU2 |
SKU3 | |
|
ARIMA |
0.84 |
0.85 |
0.89 |
|
Smoothing |
0.90 |
0.91 |
0.94 |
Другим важным свойством остатков является нормальность, поскольку подход к генерации сценариев предполагает, что остатки от нормального распределения. Для этого будет использоваться тест Шапиро-Уилка, который имеет нулевую гипотезу о том, что тестируемая выборка исходит из нормального распределения. Таблица 5 содержит p-значения остатков моделей, используемых для прогнозирования первого периода, по тесту Шапиро-Уилка. Можно увидеть высокие p-значения в строках каждой модели, что означает, что нельзя отклонить гипотезу о том, что остатки из нормального распределения.
Данные модели был оценены как визуально, так и с помощью оценок точности, а также были оценены остатки моделей с помощью статистических тестов. Экспоненциальное сглаживание и ARIMA работают лучше, чем в библиотека Prophet. Метод экспоненциального сглаживания имеет лучшие средние оценки точности, но некоторые из его прогнозов имели признаки чрезмерной подгонки. Кроме того, остаточная автокорреляционная оценка показала, что модель (или, скорее, выбор параметра) может быть дополнительно улучшена. Средний MAPE моделей ARIMA немного выше, но его средний RMSE (вычисленный из масштабированных рядов) точно такой же. Однако оценка показала, что ее остатки, вероятно, не коррелируют и могут быть из нормального распределения. Из-за его хорошей “в среднем” производительности во всех оценочных частях модель ARIMA была выбрана в качестве модели для генерации сценариев спроса для моделей запасов.
Литература:
- Подкорытова О. А., Соколов М. В. Анализ временных рядов: учебное пособие для бакалавриата и магистратуры. — 2-е изд. — М.: Юрайт, 2018. — 267 с.
- Саркисян С. А., Каспин В. И., Лисичкин В. А., Минаев Э. С, Пасечник Г. С.. Теория прогнозирования и принятия решений. — М.: «Высш. школа», 1977. — 351 с.
- Анализ временных рядов с помощью python // habr.com. URL: https://habr.com/ru/post/207160/ (дата обращения: 15.05.2019).

