Математические модели опухолей молочной железы



Введение

Среди всех злокачественных новообразований у женщин около 20–25 % составляют заболевания молочной железы. Такую же долю составляют смертные случаи. По последним статистическим данным из-за демографического подъема и геронтологической ситуации в мире к 2030 году смертность в результате онкологических заболеваний увеличится на 45 %, а число новых случаев заболеваний онкологией увеличится на 27 %. По данным Всемирной Организации Здравоохранения (ВОЗ) только в 2015 году от онкологических заболеваний погибло 8,8 млн человек.

В 2017 году на 100 000 женского населения приходилось около 450 больных с установленным диагнозом рака молочной железы. Рак молочной железы занимает первое место из всех онкологических заболеваний среди женского населения страны. Темпы роста числа больных начиная с 1990-х годов составляют около 3.5 % в год на 100 больных жителей женского населения Российской Федерации, а число больных в возрастной когорте до 35 лет увеличивается на 4.0 % в год. Это заболевание является прогрессирующим в большинстве стран мира. В некоторых странах темпы роста доходят до 6 % в год. На развитие заболеваний влияют различные причины: наследственность, сопутствующие заболевания, внешние физические факторы, депрессия, масса тела, географическое место жительства [1]. Достоверное знание этих причин позволит снизить риск заболевания. Непосредственное лечение заболеваний осуществляется различными методами [2–5], но единого мнения о наиболее эффективном методе на сегодняшний день нет. Хирургический метод — как в самостоятельном варианте, так и в комбинации с лучевой терапией, химиогормонотерапией, таргетной терапией — является основой лечения рака молочной железы химиотерапией [6]. В этом направлении при наличии хорошей математической модели можно спланировать варианты лечения и оценить его временные интервалы [7].

Онкологические заболевания являются трудноизлечимыми, с высоким уровнем смертности. Несмотря на достижения медицины в лечении онкологических заболеваний, эффективные программы выявления больных рост числа больных остановить не удается. Нет и эффективных методов лечения по некоторым специализациям заболевания. Для решения задачи защиты здоровья населения необходимы усилия в различных областях науки и практики. В этом направлении математическое моделирование позволяет оценить возможные методы лечения заболеваний. Доступность основных статистических данных по онкологическим заболеваниям в России и ее регионах обеспечивается изданиями Госкомстата РФ [8] и федерального государственного учреждения Московский научно-исследовательский онкологический институт им. П. А. Герцена [9].

Статистика онкологических заболеваний

Наибольшая смертность от различных заболеваний на протяжении последних 50 лет приходится на заболевания системы кровообращения (47 % от всех смертей). Второе место занимают онкологические заболевания — 17 %. На рис. 1 из расчета на 100 000 населения показано изменение смертности от всех причин заболеваний, от заболеваний системы кровообращения и новообразований. Статистическим данным с 1970 по 2017 год соответствует символ *. Смертность за 1970 год по всем классам причин считается равной 1. Растущую с 1970 по 2004 год смертность от всех заболеваний и от заболеваний системы кровообращения удалось остановить только к 2004 году, а затем и постоянно ее уменьшать. Смертность от новообразований, выросшую за 30 лет в 1.4 раза, уменьшить, начиная с 2004 года, не удается. Ее уровень не изменяется последние 20 лет.

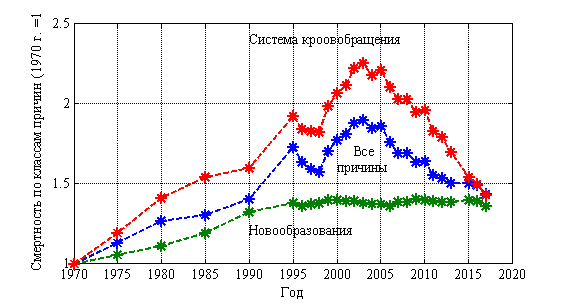
Рис. 1.

Институт Герцена в статистических данных выделяет группу лиц, впервые поставленных на учет и стоящих на учете на конец года. Динамика изменения числа лиц в этих группах (относительно числа лиц в 1970 г.) приведена на рис. 2. Статистическим данным соответствует символ *. Рост числа лиц, стоящих на учете, и лиц впервые заболевших происходит по экспоненциальной зависимости с показателем для стоящих на учете, и с для заболевших впервые.

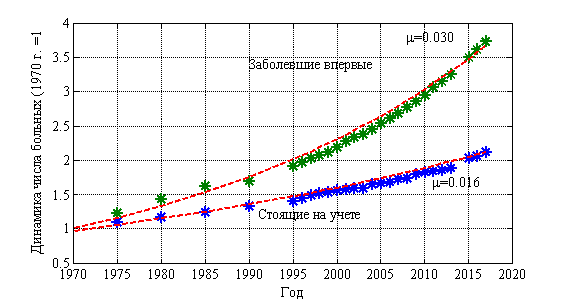
Рис. 2.

Болезни с наибольшими смертностями и темпами роста числа больных у женщины являются заболевания репродуктивной системы и онкологические заболевания. Среди онкологических заболеваний к наиболее опасным и быстро увеличивающимся числом больных относятся опухоли молочной железы. Темпы роста числа больных в этих группах отражены на рис. 3. Как следует из рис. 3 группа больных молочной железой увеличивается приблизительно на 3.5 % в год, а по отношению ко всему женскому населению — на 0.15 % в год. При таких темпах роста число женщин с онкологическим заболеваниями молочной железы к 2030 будет около 1 % всего женского населения страны.

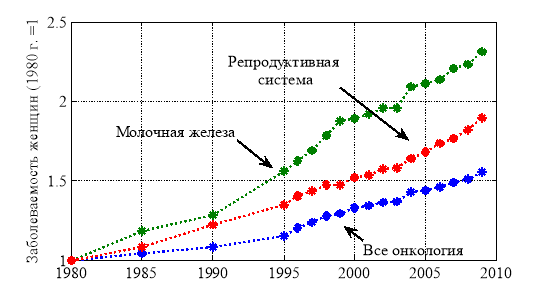
Рис. 3.

Возрастная структура онкологических больных (молочная железа) отражена на рис. 4. Пунктирная линия соответствует нормальному распределению. . На рис. 5 отражена возрастная структура смертности. Пунктирная линия соответствует нормальному распределению. . Как следует из анализа этих данных около половины больных относятся к лицам трудоспособного возраста.

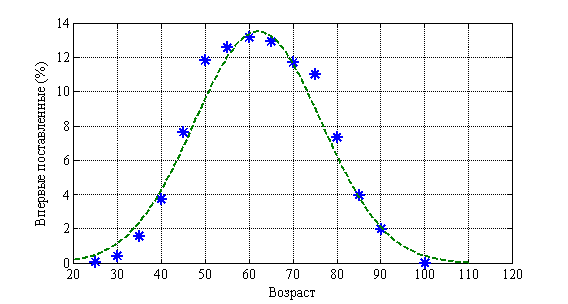
Рис. 4.

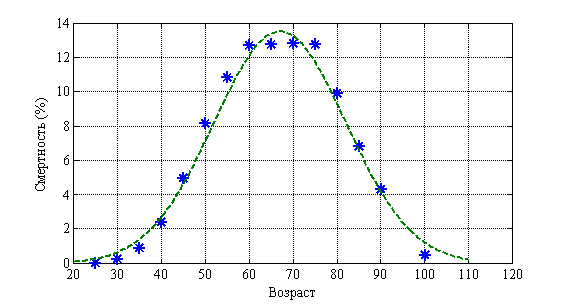
Рис. 5.

При постановке первичного диагноза у 50 % больных обнаруживаются первая и вторая стадии из четырех стадий заболеваний, у 25 % третья и 20 % четвертая. 2 % больных после постановки диагноза отказываются от лечения, а 7 % лечение существующим методам противопоказано.

Рак является прогрессирующим заболеванием в большинстве стран мира. В некоторых странах темпы роста доходят до 6 % в год. В 57 странах Европы рост числа больных раком молочной железы изменяется от 0.045 до 0.200 больных в год при среднем значении 0.082 среднеквадратичном отклонении 0.029. Динамика числа больных с 1970 по 2015 год в Финляндии, Эстонии и Швеции отражена на рис. 6. Символом «*» отмечены статистические данные. Число больных на 1970 год принято равным единице. Пунктирной линиями для Эстонии и Швеции отмечены экспоненциальные зависимости с показателями 0.019 для Швеции и с показателем 0.027 для Эстонии. Число больных в Финляндии растет с постоянной скоростью 0.09 человек в год.

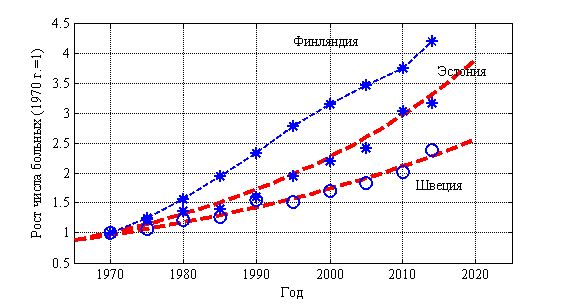
Рис. 6.

На развитие заболеваний влияют различные причины: наследственность, сопутствующие заболевания, внешние физические факторы, депрессия, масса тела, географическое место жительства [1]. Достоверное знание этих причин позволит снизить риск заболевания. Непосредственное лечение заболеваний осуществляется различными методами [7], но единого мнения о наиболее эффективном методе на сегодняшний день нет. Хирургический метод — как в самостоятельном варианте, так и в комбинации с лучевой терапией, химиогормонотерапией, таргетной терапией — является основой лечения рака молочной железы химиотерапией [7]. Наиболее распространенными методами лечения являются: хирургическое (50 % случаев), комбинированное (32 %), лучевое (11.1 %).

Строение тканей

Основной структурной единицей живого вещества является клетка — само регулируемая, самовоспроизводящаяся и само сохраняющаяся система. Как физическая система клетка представляет собой сложную систему биополимеров, отделенных от внешней среды мембраной. Межклеточное взаимодействие обеспечивает функциональную кооперацию контактирующих клеток — согласованность действия клеток в многоклеточном организме. Между клетками большинства тканей образуются микроскопические канальцы, по которым происходит перетекание вещества из одной клетки в другую. Это обеспечивает выравнивание градиентов концентрации веществ. Каналы могут закрываться на разные промежутки времени. Закрытие каналов навсегда приводит к изоляции клетки с выходом ее из-под контроля координирующих пролиферацию команд.

Процесс деления клеток сложен, состоит из нескольких циклов, регулируется каскадом команд. Каждая новая клетка делится определенное число раз с последующим самоуничтожением. Нарушение механизма самоуничтожения у части клеток приводит к их постепенному накоплению с последующим образованием «опухоли». То есть, процесс роста опухоли обусловлен избыточным воспроизводством клеток. В опухолях возникают зоны некроза на некотором расстоянии от кровеносных сосудов, по которым происходит снабжение клеток питанием. Рост опухоли сопровождается уменьшением сосудистой сети на единицу объема. Это также является фактором, увеличивающим клеточные потери и размер некротической зоны.

Наиболее цитируемой моделью опухоли является предположение о возникновении опухолевых клеток из одной клетки. Это предполагает однородность опухоли на протяжении всего времени ее роста. Однако по мере роста изменяются структурные и функциональные свойства клеток опухоли, появляется способность метастазированию, изменяется способность реагировать на гормональное влияние и химические препараты. То есть первичный клон опухолевых клеток дает начало множеству субклонов, отличающихся в функциональном отношении: реакцией на иммунный ответ, способностью к расселению, способностью к метастазированию, устойчивостью к лучевой и лекарственной терапии (рис. 7).

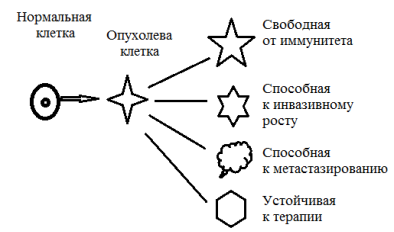
Рис. 7.

Строение молочной железы

Ткань молочной железы состоит из конусообразных долей. Каждая доля состоит из собственных долек, от которых проходят молочные протоки, заканчивающиеся млечными порами. Молочные протоки представляют собой полые нити, стенки которых состоят из эпителиальной ткани. Система из долек, молочных протоков и пор позволяет производить кормление грудью. При протоковом раке молочной железы некоторые клетки эпителиальной ткани протоков мутируют, становясь постоянно делящимися, и начинают делиться, заполняя собой просвет протока молочной железы [10, 11]. Описанная опухоль классифицируется как образование низкой степени злокачественности, которая при прогрессировании заполняет собой протоковый просвет. В этом случае опухоль развивается только в протоке, не проникая в другие ткани. Питательные вещества опухолевые клетки, как и здоровые клетки эпителия, получают через кровеносные сосуды [12, 13].

Злокачественные новообразования характеризуется активным делением клеток, сопровождающимся вытеснением нормальных клеток и накоплением атипичных. При внутрипротоковом РМЖ рост атипичных тканей происходит непосредственно внутри самих протоков. Атипичные клетки быстро делятся, и затем происходит их десквамация в полость протоков молочной железы. Клетки опухоли не поражают стенки протоков и могут распространяться внутри вдоль них.

Первые математические модели опухолей молочной железы были разработаны в 1950-е годы. В 1956 г. V. P. Collins предложил экспоненциальную модель развития опухоли. L. von Bertalanffy в 1957 году предложил строить модели развития рака молочной железы с учетом размеров и обменных процессов внутри самой опухоли. A. K. Laird в 1964 году при описании роста РМЖ впервые использовал модель Гомперца. J. A. Spratt с группой ученых в 1993 году впервые предложили логистическую модель роста новообразования молочной железы. В основе сегодняшних моделей лежит предположение о случайном смещении всех взаимодействующих клеток опухоли за счет диффузии или учитывается диффузионное движение и гидродинамическое смещение, вызванное избыточным внутренним давлением при росте опухоли [16–21]. В работе предлагается диффузионная модель, в которой учитываются только три типа клеток — «опухолевые» (делящиеся), «нормальные» и «некротические».

Математическая модель зарастания протоки молочной железы

Проток молочной железы рассматривается как цилиндрическая трубка длиною с радиусом , в которой находятся клетки эпителия и клетки опухоли с линейными плотностями и , соответственно. Распространение опухоли вдоль протока происходит за счет диффузии клеток опухоли, тогда как клетки эпителия не распространяются по протоку. Клетки опухоли оказывают угнетающее влияние на клетки эпителия. Геометрический объем функционально пространства, в котором происходит рост опухолевых клеток принимается равным единице. Поскольку радиус трубки значительно меньше ее длины, геометрической моделью протока является отрезок длиной . Математическая модель роста опухоли представлена краевой задачей для системы двух дифференциальных уравнений в частных производных

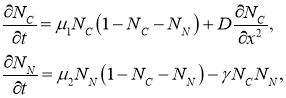(1)

где — время, — пространственная координата.

К системе уравнений (1) добавляются условия на границах отрезка при и :

, ,

и начальные условия при :

, при и при .

Граничные условия соответствуют свободному росту опухоли вдоль отрезка. Начальные условия предполагают, что при в функциональном пространстве находятся «здоровые» клетки, а в точке появляется небольшое количество опухолевых клеток. Поскольку объем функционального пространства, в котором находятся клетки, принят за единицу, то там, где пространство полностью заполнено клетками (при выполнении равенства ), их рост прекращается. В этой модели предполагается, что опухолевые клетки оказывают стрессовое влияние на «здоровые» клетки со скоростью . и — удельные скорости роста опухолевых и здоровых клеток соответственно.

Локальная модель

В этой модели считается, что и общее количество клеток на отрезке. С учетом этого из (1) при следует система обыкновенных дифференциальных уравнений

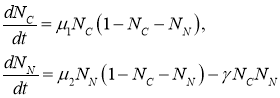(2)

с начальными условиями

, , где — малая величина.

Для матрицы Якоби правой части системы уравнений (2) справедливо выражение

.

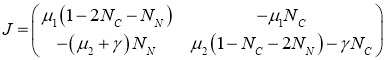Система уравнений (2) имеет три стационарные точки.

1. , .

В этой точке оба собственных значения и матрицы положительные. Поэтому в соответствии с теоремой Ляпунова об устойчивости стационарных точек эта стационарная точка будет неустойчивой.

2. , .

В этой точке оба собственных значения и матрицы отрицательные. Отрицательность собственных значений обеспечивает устойчивость этой стационарной точки.

3. , .

В этой точке и . Поскольку одно собственное значение равно нулю, то из линейного приближения устойчивость этой стационарной точки не следует.

Из уравнений (2) следует, что

.

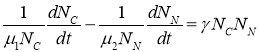Поскольку правая часть этого равенства является положительной функцией, то скорость роста функции должна быть положительной. Поэтому третья стационарная точка должна быть неустойчивой.

Решение системы уравнений (2) осуществлялось с применением численных методов. На рис. 8 для случая , , отражено изменение функций и во времени. Принято, что поскольку считается, что удельная скорость опухолевых клеток выше, чем нормальных [13, 14]. Полученный результат соответствует клиническому этапу роста опухоли около пяти лет (1700 дней).

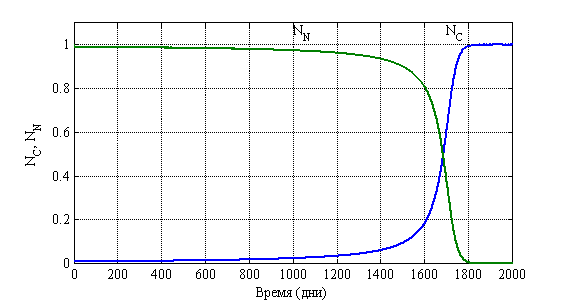
Рис. 8. Зависимость функций и при , , .

Модель статистики заболеваемости

Скорость зарастания протока у каждого больного индивидуальна. Примем, что в модели (2) это отражается в различных значениях параметров , и . Пусть , минимальные значения этих параметров («базовые»), которые могут быть у «больного». Примем, что для остальных «больных» эти параметры распределены случайным образом:

, (),

где , и случайные числа из промежутка , — положительная величина, характеризующая степень отклонения параметров от «базовых».

Тогда интегрирование уравнений раз (для больных) позволит оценить вероятную статистику степени заболеваемости. По степени заболеваемости «больных» разделим на четыре группы. В заданный момент времени в первую группу относятся «больные», у которых , во вторую — , в третью — , в четвертую — .

На рис. 9 приведено распределения значений в момент времени в зависимости от числа случаев из 10 000 для случая , , . На рис. 10 показано изменения числа случаев четвертой стадии в долях от 10 000 случаев во времени. На рис. 11 приведено распределение больных по стадиям в момент времени , а на рис. 12 в момент времени . На рис. 13 отражено изменение среднего значения для 10 000 экспериментов (среднее), а также минимального и максимального для каждого из 10 000 случаев в каждый момент времени.

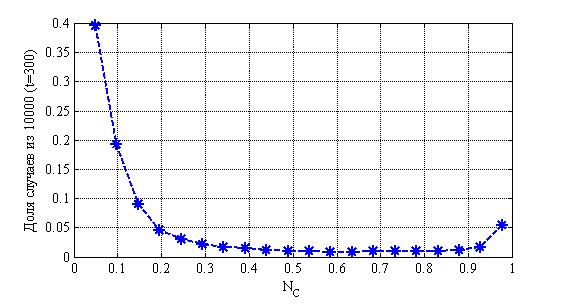
Рис. 9. Распределения значений в момент времени в зависимости от числа случаев

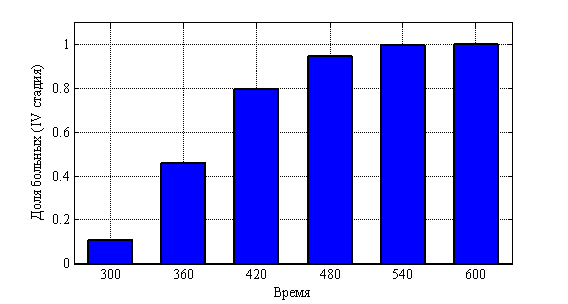
Рис. 10. Динамика числа «больных» в четвертой стадии

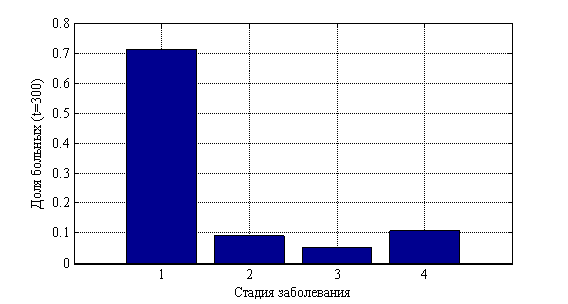
Рис. 11. Распределение «больных» по стадиям в момент времени

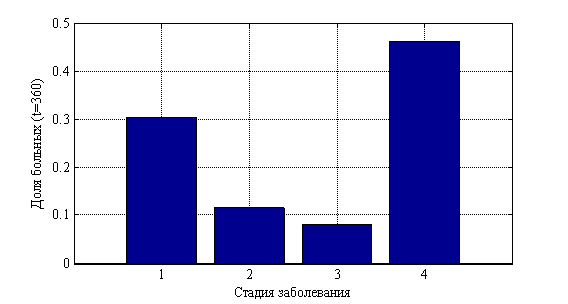
Рис 12. Распределение «больных» по стадиям в момент времени

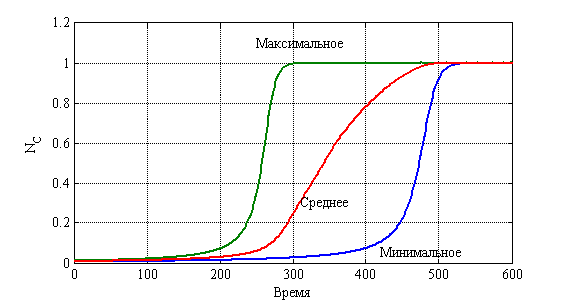
Рис. 13. «Статистический» диапазон изменения

Модель лечения

Лечение опухолей осуществляется с применением различных методов: хирургическое вмешательство, химиотерапия, радиоиммунотерапия, криогенная и таргетная технологии [10]. Но основным методом является хирургический метод с последующей химиотерапией [7]. Поскольку хирургическое вмешательство является практически «мгновенным», по сравнению со временем проведения последующей химиотерапии, то в работе рассматривается вариант только химиотерапии.

В клинической практике лечение начинается в момент постановки диагноза. То есть на момент достоверного обнаружения опухоли. По данным [7] в клинической практике опухоль, достигшая 75 %-80 % размеров опухоли летального исхода, считается достоверно определяемой. Хирургическое вмешательство с последующей химиотерапией обеспечивают послеоперационную без рецидивной выживаемости от 5 лет и выше [22]. Химиотерапия осуществляется периодическим введением лекарств до прекращения заболевания, определяемого диагностическими методами [2, 23, 24].

В модели предполагается, что препараты действуют непосредственно только на опухолевые клетки, уничтожая их. При этом одна часть препаратов расходуется на уничтожение опухолевых клеток, а вторая распадается или отторгается организмом [25], не вступая в реакцию уничтожения опухолевых клеток. С учетом этих предположений модель (2) химиотерапии принимает вид

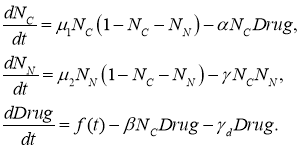(3)

Третье уравнение в (3) описывает изменение концентрации химиопрепаратов. Слагаемое в этом уравнении — скорость расхода препаратов при уничтожении опухолевых клеток, — скорость распада лекарств [26], — программа введения препаратов. В первом уравнении — скорость гибели опухолевых клеток под действием препаратов. , и — постоянные коэффициенты, характеризующие скорости реакций. Расход лекарств подсчитывается по формуле .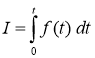

При постоянном действии препаратов таком, что в стационарной точке системы уравнений (3)

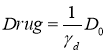, (4)

собственными значениями матрица Якоби правой части уравнений (3) будут

, , .

То есть эта стационарна точка будет устойчивой.

В стационарной точке

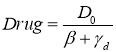, , (5)

одно из собственных значений матрицы Якоби , а два других находятся как решение уравнения

,

корни которого либо отрицательные, либо комплексно сопряженные с отрицательной вещественной частью.

Таким образом, стационарное состояние (4) с малым количеством опухолевых клеток может быть устойчивым только в случае постоянного действия препаратов. Также будет устойчивым и стационарное состояние (5) с малым количеством нормальных клеток при небольшом количестве препаратов. То есть модель (3) описывает случаи функционирования организма только при постоянном применении лекарств. Аналогичные результаты в случае многократного введения лекарств получены в [27].

Программа «лечения» начинается в момент времени , когда функция достигнет пороговое значение (уровень диагностического определения заболевания), и прекращается при выполнении условия (уровень диагностического определения окончания заболевания). При выполнении последнего условия пороговое значение уменьшается в два раза. То есть считается, что повторное обнаружение роста опухолевых клеток будет определено при меньших ее размерах, чем при первом обнаружении. Поэтому пороговое значение для функции для рецидива уменьшается.

На рис. 14 для случая , , , , отражено изменение функций и во времени. Функция задавалась следующим образом:

, если ,

, если .

Этот вариант соответствует случаю ежедневной терапии в течении 100 дней с последующим возобновлением ее через 100 дней, если опухоль начнет новый рост.

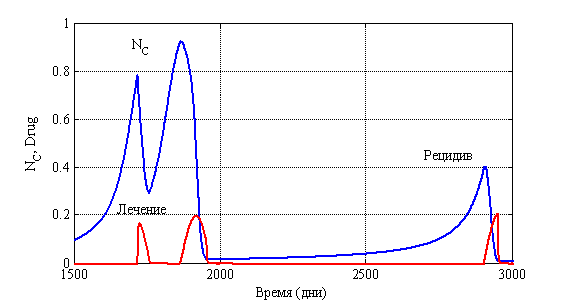
Рис. 14. Зависимость функций и при , , , , ,

Автоволновое решение

Эволюционные уравнения могут иметь автоволновые решения на бесконечной прямой [18]. В этом случае решение уравнений (1) ищется в виде функции, зависящей от одного аргумента : , . Такое решение должно удовлетворять системе уравнений

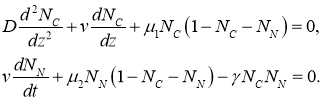(6)

В окрестности точки должны выполняться условия

, .

Малые возмущения и в окрестности этой стационарной точки такие, что и , в линейном приближении удовлетворяют системе уравнений

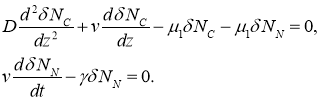
Характеристические значениями этой системы линейных уравнений будут

, .

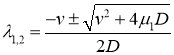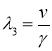В окрестности этой точки функция должна убывать, а функция возрастать. Среди трех характеристических значений два положительные и одно отрицательное. Поэтому можно построить решение системы уравнений (6), удовлетворяющее этим условиям в окрестности точки .

При должны выполняться условия

, .

Малые возмущения и в окрестности этой стационарной точки такие, что и , в линейном приближении должны удовлетворять системе уравнений

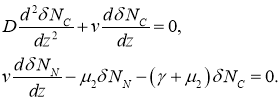
Характеристические значениями этой системы линейных уравнений будут

, , .

Среди трех характеристических значений одно положительное и одно отрицательное. В окрестности этой точки функция должна возрастать, а функция убывать. Поэтому можно построить решение системы уравнений (6), удовлетворяющее этим условиям в окрестности точки . Таким образом, система уравнений (1) может иметь автоволновое решение. Причем скорость его распространения не ограничена снизу.

Решение системы нелинейных разрешающих уравнений (1) осуществлялось с применением метода конечных разностей. Вариант значений констант выбирался исходя из опубликованных в [26, 28] данных. Для случая , , , на рис. 15 отображена зависимость функции в моменты времени , а функции только в момент времени . Единица измерения по оси абсцисс соответствует сантиметрам. Как следует из этого результата решение разрешающей системы уравнений представляет собой автоволну, распространяющуюся с постоянной скоростью. Решение строилось с применением метода сеток [20]. Результаты решения при 250 и 500 отрезках разбиения интервала интегрирования отличались не более чем на 2 % в максимальных отклонениях.

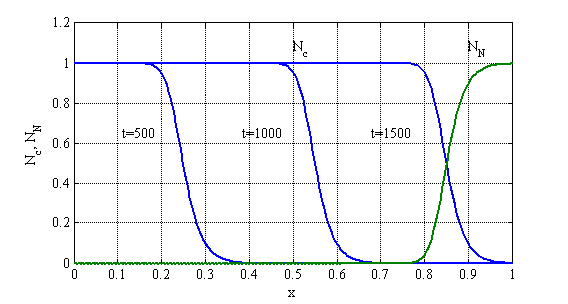
Рис. 15. Зависимость функции в моменты времени и функции в момент времени .

Как следует из полученных результатов при заданных удельных скоростях роста опухолевых и нормальных клеток и коэффициенте подвижности опухолевых клеток размер опухоли 0.9 см достигается в момент времени . Этот размер считается диагностическим определимым на основе клинических исследований [8].

Модель протокового рака молочной железы

В модели новообразования в протоке молочной железы учитывает три типа клеток: нормальные, делящиеся и некротические клетки. Делящимися клетками считаются клетки с нарушенным механизмом апоптоза, которые постоянно делятся. Некротические клетки — погибшие клетки, не несущие функциональной нагрузки. Предполагается, что делящиеся клетки оказывают стрессовое влияние на нормальные клетки [14, 15], а некротические — на нормальные и делящиеся. В отсутствии делящихся и некротических клеток в функциональном пространстве находятся только нормальные клетки. Появление делящихся или некротических клеток должно приводить в конечном итоге к гибели и нормальных, и делящихся клеток, если не учитываются факторы, влияющие на гибель делящихся клеток и на удаление из функционального пространства некротических клеток. Размер функционального пространства, в котором находятся только нормальные клетки, или только некротические клетки, принимается равным единице. То есть считается, что в отсутствие некротических и делящихся клеток концентрация нормальных клеток равна единице, такой же будет после гибели нормальных и делящихся клеток концентрация некротических клеток.

Период удвоения делящихся клеток по разным оценкам составляет от 3 до 120 дней. Однако эти оценки получены в клинической практике на очень коротком промежутке наблюдения за ее ростом. Критическая масса достигается по данным [21] при 40 удвоениях. Таким образом, удельная скорость роста опухоли в предположении ее экспоненциального роста может изменяться от 0.001 до 0.25 1/день. Делящиеся клетки имеют меньшую потребность в факторах роста, определяющих скорость их роста, чем нормальные клетки. Соответственно и удельная скорость роста нормальных клеток будет меньше, чем делящихся клеток. Сопротивление опухолевому росту оказывают лимфоциты, которые могут уничтожить небольшое количество делящиеся клетки.

У делящихся клеток нарушен механизм формирования механических контактов, силы адгезии с окружающими клетками малы, по сравнению с нормальными, они свободно распространяются в зоне их формирования. Поэтому подвижностью нормальных и некротических клеток по сравнению с подвижностью делящихся можно пренебречь. Перемещение делящихся клеток происходит по градиенту их концентрации в направлении их меньшей концентрации.

С учетом всех этих факторов математическая модель роста новообразования имеет вид

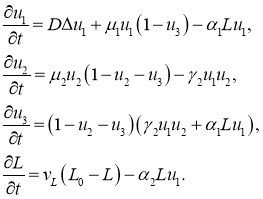(7)

В этих уравнениях , и — концентрации нормальных, делящихся и некротических клеток, — концентрация лимфоцитов, — концентрация лимфоцитов в отсутствие делящихся и некротических клеток. Слагаемое в первом уравнении в (7) является скоростью размножения делящихся клеток, которая ограничена численностью некротических клеток, слагаемое — скорость уничтожения делящихся клеток лимфоцитами. Во втором уравнении в (8) — скорость размножения нормальных клеток при условии занятия части функционального пространства некротическими клетками, — скорость гибели нормальных клеток при контакте их с делящимися клетками. Скорость увеличения численности некротических клеток пропорциональна скоростям гибели нормальных и делящихся клеток, но их рост прекращается, если они заполняют все функциональное пространство. В четвертом уравнении — скорость уменьшения численности лимфоцитов, уничтожающих делящиеся клетки. , , , и — постоянные величины, характеризующие скорости взаимодействия клеток, — скорость поступления лимфоцитов. Предполагается, что нормальные и некротические клетки в функциональном пространстве не перемещаются, делящиеся клетки перемещаются по градиенту их концентрации ( — параметр характеризующих их подвижность), а лимфоциты поступают во все точки функционального пространства.

К системе уравнений (7) добавляются граничные и начальных условия. В качестве граничных условий принимаются условия Неймана. Считается, что в начальный момент времени концентрация некротических клеток равна нулю, концентрация делящихся клеток равна единице во всех точках функционального пространства. Небольшое количество делящихся клеток возникает в малой окрестности точки с координатами в функциональном пространстве.

Локальная модель

Модель представлена системой обыкновенных дифференциальных уравнений

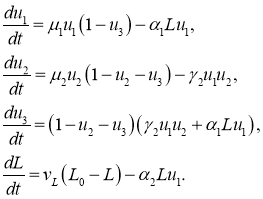(8)

В качестве начальных условий принимаются

, , , ,

где . То есть считается, что в начальный момент времени возникает небольшое количество делящихся клеток.

Система уравнений (9) имеет две стационарные точки, в которых :

, , , ,

соответствующая отсутствию делящихся и некротических клеток, и

, , , ,

соответствующая полному замещению в функциональном пространстве делящихся и нормальных клеток некротическими.

В первой стационарной точке из (8) с точностью до величин второго порядка малости для первого, второго и четвертого уравнений, и с точностью до величин второго порядка малости следуют уравнения для возмущений , , и

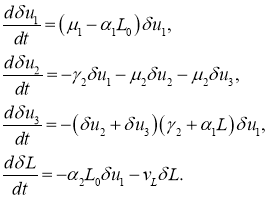
При выполнении неравенства правые части этой системы уравнений будут отрицательными. То есть малые возмущения решения в окрестности первой стационарной точки будут убывающими функции и, соответственно, эта стационарная точка будет устойчивой. То есть увеличение числа делящихся клеток может происходить только в случае выполнения условия

Во второй стационарной точке уравнения для возмущенного состояния положения равновесия приводятся к виду

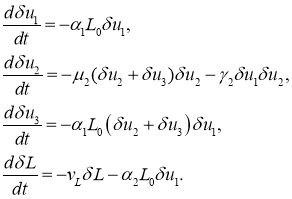
Из первого и четвертого уравнений следует, что и будут убывающими функциями. Из второго и третьего уравнений следует, что

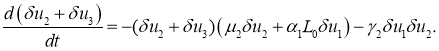
Поскольку в окрестности этой стационарной точки возмущения и должны быть положительными, то из этого уравнения следует, что сумма со временем стремиться к нулю независимо от знака возмущения . То есть, эта стационарная точка устойчивая.

На рис. 16 отражены зависимости функций , и от времени при значениях постоянных , , , , , , и начальных данных при : , , . Время соответствует годам.

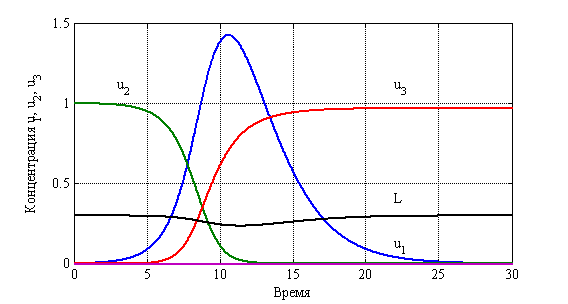
Рис. 16. Зависимость функций , и от времени

Автоволновое решение

Решение уравнений (8) на бесконечной прямой ищется в виде функции, зависящей от аргумента . То есть в виде волны, распространяющейся от к со скоростью . С учетом этого система уравнений (7) для такого решения принимает вид

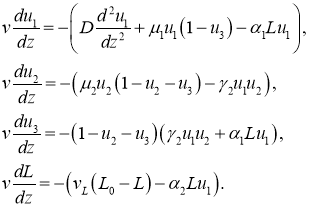(9)

К этой системе уравнения добавляются граничные условия

при :

, , , ;(10)

при :

, , , .(11)

В окрестности точки в первом приближении с точностью до величин второго порядка малости для первого, второго и третьего уравнений и второго порядка для третьего уравнения в (8) эта система уравнений приводится к виду

где , , малые по сравнению с единицей, а по сравнению с величины. Как следует из второго, третьего и четвертого уравнений , и в окрестности этой точки будут возрастающими функциями. Характеристическое уравнение первого уравнения

имеет корни противоположных знаков. Поэтому в окрестности этой точки можно построить решение, на котором будет убывающей функцией.

В окрестности точки в первом приближении с точностью до величин второго порядка малости система уравнений (8) приводится к виду

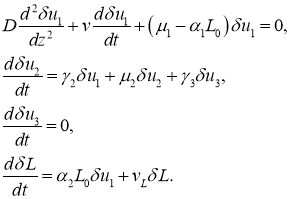
В окрестности этой точки функции и возрастающие функции, не изменяется. Характеристическое уравнение первого уравнения

будет иметь вещественные корни противоположных знаков, если выполняется неравенство . В этом случае в окрестности этой точки можно построить решение, на котором будет убывающей функций. Таким образом, при выполнении условия

(12)

может существовать автоволновое решение уравнений (7), удовлетворяющее условиям (10) и (11). Полученная количественная оценка существования автоволнового решения в рамках модели злокачественной опухоли протока молочной железы естественно сопоставлять со скоростью роста опухоли вдоль протока. При этом эта скорость тем выше, чем выше удельная скорость роста делящихся клеток, и тем меньше, чем больше скорость их уничтожения лимфоцитами.

Ограниченный отрезок

Для случая распространения делящихся клеток на отрезке длины к системе уравнений (7) добавляются граничные условия

при и :

,(13)

и начальные условия при :

.(14)

Система уравнений (7) при этих граничных условий имеет стационарное решение

, , , . (15)

При малых возмущениях , , этого положения равновесия первое уравнение в (8) с точностью до величин второго порядка малости принимает вид

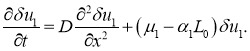
Этому уравнению при рассматриваемых начальных условиях удовлетворяет функция

,

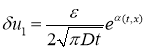где

.

Как следует из анализа этого решения при выполнении неравенства в линейном приближении распространение делящихся клеток на отрезке происходит со скоростью . Положение равновесия (15) в этом случае будет неустойчивым.

Система уравнений (8) при этих граничных условиях имеет стационарное решение

, , , .

При малых возмущениях этого положения равновесия первое уравнение в (7) в линейном приближении приводится к виду

.

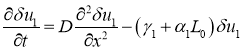Решение этого уравнения при граничных условиях (14) при любых малых начальных положительных значениях будет убывающей функцией времени. То есть это положение равновесия будет устойчивым.

Численное решение системы уравнений (7) при этих граничных условиях при и

и начальных условиях

, , ,

строилось с применением метода сеток. Осуществлялась дискретизация системы уравнений (7) по пространственным и временным переменным. Полученная система нелинейных уравнений решалась с применением метода простой итерации. Итерационный процесс на каждом временном шаге прекращался, если была достигнута заданная точность на двух соседних итерациях. Для отрезка единичной длины решение на 200 и 500 отрезах разбиения совпадало с точностью, не превышающей 1 % в точках максимальных отклонений. Шаг по временной переменной выбирался из условия , где — шаг по пространственной переменной. Результаты решения для случая , , , , , , , , представлены на рис 17 в виде зависимостей в момент времени , и зависимостей , и в момент времени . Скорость распространения делящихся клеток вдоль отрезка оценивается по расстоянию между точками максимума в зависимостях отнесенное к промежутку между временами их достижения. В расчетах она практически совпадает с теоретической ее оценкой (12) следующей из условия существования автоволнового решения (). Этот результат согласуется аналогичными результатами, полученными при моделировании различных биохимических реакций.

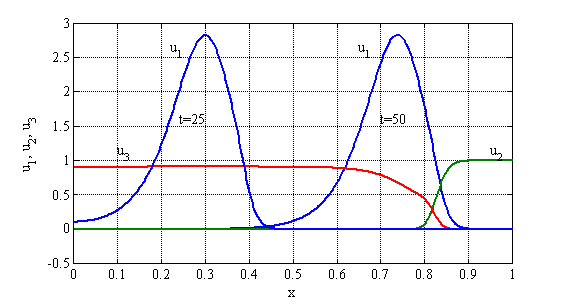
Рис. 17.

Заключение

Анализ статистических данных динамике числа больных, показывает увеличение крупы риска больных злокачественными опухолями молочной железы на 3–4 % в год в большинстве стран Европы, включая Российскую Федерацию. Число больных онкологическими заболеваниями женщин может достигнуть 1 % к 2020 году. Разработанные математические модели позволяют оценить различные программы лечения и дать оценку экономических затрат на лечение и профилактику заболеваний.

Литература:

1. Kolpak E. P, Frantsuzova I. S. Causes of morbidity and mortality from breast cancer // Eurasian Journal of Analytical Chemistry. — 2017. — Т. 12. — № 5b. С. 779–791.
2. Абакушина Е. В., Абакушин Д. Н., Анохин Ю. Н. Экспериментальные и клинические подходы к радиоиммунотерапии в онкологии // Сибирский онкологический журнал. — 2014. — № 3. С. 56–64.
3. Клименко Ш. М., Хаджиматова А. И., Целуйко С. С. Оценка изменения морфологических и иммуногистохимических характеристик карцином молочной железы при проведении неоадъювантной системной терапии // Опухоли женской репродуктивной системы. — 2018. — Том 14. — № 1. С. 12–19.
4. Кухарев Я. В., Стахеева М. Н., Дорошенко А. В., Литвяков Н. В., Бабышкина Н. Н., Слонимская Е. М., Чердынцева Н. В. Связь иммунологических показателей с эффективностью неоадъювантной химиотерапии у больных раком молочной железы // Сибирский онкологический журнал. — 2013. — № 2 (56). С. 50–57.
5. Чернов В. И., Брагина О. Д., Синилкин И. Г., Тицкая А. А., Зельчан Р. В. Радиоиммунотерапия в лечении злокачественных образований // Сибирский онкологический журнал. — 2016. Том 15. — № 2. С. 101–106. DOI: 10.21294/1814–4861–2016–15–2-101–106.
6. Трофимова О. П., Волкова Н. В., Назаренко А. В., Колядина И. В., Хайленко В. А., Ткачев С. И., Прямикова Ю. И., Тимошкина Е. В., Зайченко О. С., Болдырева В. А., Воротников И. К., Алиева С. Б., Борисова Т. Н., Глебовская В. В., Иванов С. М. Результаты лечения больных ранним раком молочной железы по методу ускоренного частичного облучения после органосохраняющих операций. Опыт ФГБУ «НМИЦ онкологии им. Н. Н. Блохина» Минздрава России // Опухоли женской репродуктивной системы. — 2017. — Том 13. — № 4. С. 10–18.
7. Пак Д. Д., Болотина Л. В., Сухотько А. С. Современные принципы комплексного лечения генерализованного рака молочной железы (обзор литературы и анализ собственного материала) // Сибирский онкологический журнал. — 2013. — № 5 (59). С.54–58.
8. Российский статистический ежегодник. 2014: Стат.сб./Росстат. М., 2014. — 693 с.
9. Состояние онкологической помощи населению России в 2014 году. М.: МНИОИ им. П. А. Герцена филиал ФГБУ «НМИРЦ» Минздрава России, 2015. - 236 с.
10. Пак Д. Д., Рассказова Е. А., Данилова Т. В. Подтипы рака молочной железы // Опухоли женской репродуктивной системы. — 2012. — № 3–4. С. 13–18.
11. Стенина М. Б., Царева Е. В., Жаров А. А., Тюляндин С. А. Инфильтрирующие опухоль лимфоциты: биологическая суть и клиническое значение при раке молочной железы // Российский онкологический журнал. — 2016. ‑№ 21 (1–2). DOI: 10.18821/1028–9984–2016–21–1-92–100.
12. Лаптиев С. А., Корженевская М. А., Имянитов Е. Н. Молекулярно-генетический «портрет» рака молочной железы // Ученые записки СПбГМУ им. акад. И. П. Павлова. — 2017. — № 24(2). С. 12–22. DOI: 10.24884/1607–4181–2017–24–2-12–22.
13. Иванов В. Г. Эпидемические факторы риска, ранняя диагностика рака молочной железы // Лекции по фундаментальной и клинической онкологии. / Под ред. В. М. Моисенко, А. Ф. Урманчеевой, К, П. Хансона. СПб: ООО Издательство Н-Л., 2004. — 704. С. 213–221.
14. Моисеенко В. М. «Естественная история» рака молочной железы // Эпидемические факторы риска, ранняя диагностика рака молочной железы // Лекции по фундаментальной и клинической онкологии. / Под ред. В. М. Моисенко, А. Ф. Урманчеевой, К, П. Хансона. СПб: ООО Издательство Н-Л., 2004. — 704. С. 198–212.
15. Harald Weedon-Fekjær, Bo H Lindqvist, Lars J Vatten, Odd O Aalen, Steinar Tretli Breast cancer tumor growth estimated through mammography screening data // Breast Cancer Research 2008, 10:R41 (doi:10.1186/bcr2092).
16. John Carl Pane’ita A Mathematical Model of Breast and Ovarian Cancer Treated with Paclitaxel // Mathematical biosciences. — 1997. — № 146. С. 89–113.
17. Franks S. J., Byrne H. M., King J. R., Underwood J. C. E., Lewis C. E. Modelling the early growth of ductal carcinoma in situ of the breast // J. Math. Biol. 2003. — № 47 С. 424–452. DOI: 10.1007/s00285–003–0214-x.
18. Кузнецов М. Б., Колобов А. В. Исследование влияния антиангиогенной монотерапии на прогрессию гетерогенной опухоли с помощью методов математического моделирования // Компьютерные исследования и моделирование. — 2017. — Т. 9. — № 3 С. 487–501. DOI: 10.20537/2076–7633–2017–9-3–487–501.
19. Колобов А. В., Кузнецов М. Б. Математическое моделирование роста малоинвазивной опухоли с учетом инактивации антиангиогенным препаратом фактора роста эндотелия сосудов // Компьютерные исследования и моделирование. — 2015. — Т. 7. — № 2. С. 361–374.
20. Wise S. M., Lowengrub J. S., Frieboes H. B., Cristini V. Three-dimensional multispecies nonlinear tumor growth–I. Model and numerical method // J Theor Biol. — 2008. № 253(3). С. 524–543. doi:10.1016/j.jtbi.2008.03.027.
21. Ying Chen, John S. Lowengrub Tumor growth in complex, evolving microenvironmental geometries: A diffuse domain approach // J Theor Biol. — 2014. — № 361. С. 14–30. doi:10.1016/j.jtbi.2014.06.024.
22. Башлык В. О., Хаджиматова Ш. М., Криворотько П. В., Артемьева А. С., Кудайбергенова А. Г. Клеточная плотность и пролиферативная активности в промежуточных биоптатах рака молочной железы при неоадъювантной химиотерапии // Злокачественные опухоли. — 2016. — № 4-S1 (21). С. 136
23. Бабушкина Н. А., Глумов В. М., Кузина Е. А. Применение математического моделирования для оценки эффективности противоопухолевых вирусных вакцин // Проблемы управления. — 2017. — № 3. С. 49–56.
24. Andrey, Z.V.^, Konstantin, G. G. Simulation of targeted transport for drug substances part 1: A single administration // Siberian Journal of Oncology. — 2017. — № 16 (1). С. 59–65. DOI: 10.21294/1814–4861–2017–16–1-59–65.
25. Terisse Brocato, Prashant Dogra, Eugene J. Koay, Armin Day, Yao-Li Chuang, Zhihui Wang, Vittorio Cristini Understanding Drug Resistance in Breast Cancer with Mathematical Oncology // Curr Breast Cancer Rep. — 2014. № 6. С. 110–120. DOI 10.1007/s12609–014–0143–2.
26. Hildur Knútsdóttir, EirikurPálsson, Leah Edelstein-Keshet Mathematical model of macrophage-facilitated breast cancer cells invasion // Journal of Theoretical Biology. — 2014. — № 357. С. 184–199. http://dx.doi.org/10.1016/j.jtbi.2014.04.031 0022–5193.
27. Zaborovskiy A. V., Gurevich K. G. Modeling of targeted drug delivery part II. Multiple drug administration // Siberian journal of oncology. — 2017. — № 16(2). С. 36–41. DOI: 10.21294/1814–4861–2017–16–2-36–41.
28. Jan Lankelma, Rafael Ferna´ndez Luque, Henk Dekker, Wim Schinkel, Herbert M. Pinedo A Mathematical Model of Drug Transport in Human Breast Cancer // Microvascular Research. — 2000. № 59. С. 149–161. doi:10.1006/mvre.1999.2218, http://www.idealibrary.com on.