Эффективность применения современных силовых устройств гибкого регулирования (FACTS), основанных на широком применении преобразовательной техники, предлагается выполнять на базе простых моделей, с приемлемой точностью воспроизводящих их внешние характеристики. Более подробно были рассмотрены модели двух устройств: СТАТКОМа и ОРПМ. Моделирование СТК двустороннего действия и УШР, включающего в свой состав нерегулируемую батарею конденсаторов, произведено с помощью управляемой проводимости, с учетом запаздывания в случае необходимости. Полученные результаты используются только для сравнения.
Математическая модель СТАТКОМ
Электромеханические переходные процессы электроэнергетической системы с учетом регулируемого устройства типа СТАТКОМ могут быть определены из следующей динамической модели, описанной системой алгебро-дифференциальных уравнений.
Входной переменной является напряжение на шинах высокого напряжения сети в точке подключения устройства Uст, заданное своими проекциями Uq и Ud на координатные оси q и d.
Проводимость СТАТКОМа, соответствующая, как и ранее, индуктивным сопротивлениям согласующего трансформатора и сглаживающего реактора (xΣ= 0,2), принимается в относительных единицах равной
bст = Sст/0,2.
Мощность СТАТКОМа Sст задается в исходных данных.
Приращение ЭДС СТАТКОМа ΔEст вычисляется на основе следующей передаточной функции:
![]()
где Uуст — напряжение уставки,
Kst–коэффициент регулированияканала отклонения напряжения (Kst = -1…-10),
Tv — постоянная времени канала отклонения напряжения (Tv = 0,001 с).
Величина приращения ЭДС ограничивается на уровне 0,2 о.е., следовательно, модуль тока СТАТКОМа, равный произведению ∆𝐸ст ∙ 𝑏ст не может превысить заданной в относительных единицах величины Sст.
Поскольку при моделировании используется общая координатная система q,d, связанная с математической моделью генератора, то вычисляются коэффициенты распределения приращения ЭДС по осям q и d:
Kq = abs (Uq)/Ug,
Kd = abs (Ud)/Ug.
D, q — составляющие токов СТАТКОМа вычисляются в соответствии с соотношениями, связывающими составляющие его ЭДС и напряжения на его зажимах:
𝐼𝑞ст + 𝑗𝐼𝑑ст = (𝐸𝑞ст + 𝑗𝐸𝑑ст − 𝑈𝑞 − 𝑗𝑈𝑑) ∙ 𝑗𝑏ст,
откуда следует, что
𝐼𝑞ст = −𝑏ст ∙ (𝐸𝑑ст − 𝑈𝑑),
𝐼𝑑ст = 𝑏ст ∙ (𝐸𝑞ст − 𝑈𝑞).
Выражения в круглых скобках представляют собой проекции приращений ЭДС СТАТКОМа соответственно на d и q координатные оси, поэтому q,d — составляющие токов вычисляются по выражениям:
𝐼𝑞ст = − 𝑏ст ∙ ∆𝐸ст ∙ 𝐾𝑑 ∙ 𝑠𝑖𝑔𝑛(𝑈𝑑),
𝐼𝑑ст = 𝑏ст ∙ ∆𝐸ст ∙ 𝐾𝑞 ∙ 𝑠𝑖𝑔𝑛(𝑈𝑞).
Непосредственное использованиерезультатов вычисления токов по алгебраическим выражениям, в балансе токов в узле подключения СТАТКОМа приводит к вычислительной неустойчивости, поэтому значения, участвующие в вычислительном процессе, определяются с помощью передаточных функций:
![]()
![]()
где Ti — постоянная времени, определяющая запаздывание реакции СТАТКОМа на изменение управляющего воздействия по каналу регулирования ЭДС, обычное значение Ti = 0,0033…0,01 с.
Математическая модель ПСТАТКОМа
Для выполнения расчетов электромеханических переходных процессов электроэнергетической системы с учетом регулируемого устройства типа ПСТАТКОМ может быть предложена следующая динамическая модель, описываемая системой алгебро-дифференциальных уравнений. Предполагается, что устройство работает в составе объединенного регулятора перетока мощности (ОРПМ), включающего в себя СТАТКОМ, который передает ПСТАТКОМу определенную величину активной мощности (в соответствии с собственным режимом работы). Совместная работа двух устройств отражена в системе ограничений с учетом возможности независимой генерации устройствами реактивных мощностей.
Входной переменной является значение тока, протекающего по включенному последовательно в линию электропередачи трансформатору в точке подключения устройства Im, заданное своими проекциями Iq и Id на координатные оси общей координатной системы q и d.
Индуктивное сопротивление трансформатора ПСТАТКОМа принимается в относительных единицах равным xпст = 0,04 …0,1 о.е.
Мощность ПСТАТКОМа Sст задается в исходных данных.
Сигнал управления ЭДС ПСТАТКОМа вычисляется по известному отклонению тока с помощью следующей передаточной функции:
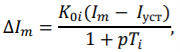
где Iуст — ток уставки,
K0i — коэффициент регулированияканала отклонения тока (K0i = -1…-10),
Ti — постоянная времени канала отклонения тока (Ti = 0,01 с).
D, q — составляющие ЭДС ПСТАТКОМа вычисляются с использованием передаточных функций с учетом дополнительного сигнала управления по отклонению скольжения s ротора генератора относительно синхронной оси:
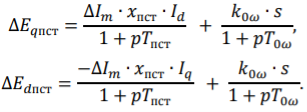
Величины приращений добавочных напряжений ПСТАТКОМа вычисляются по полученным составляющим ЭДС с учетом ограничений, определяемых возможностями передачи мощности от СТАТКОМа в соответствии с его загрузкой; ограничивается на уровне разности комплексных мощностей Sпст=|Sст_max — Scт|, таким образом, приращения напряжений, вносимые ПСТАТКОМом, не превышают заданных величин, соответствующих мощности Sпст_max и величине мощности, поступающей со стороны СТАТКОМа. Для этого рассчитываются коэффициенты распределения в координатной системе q,d:
Kq = abs (Iq)/Im,
Kd = abs (Id)/Im.
D, q — составляющие напряжений ПСТАТКОМа вычисляются в соответствии с ограничениями:
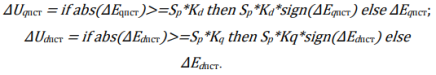
Непосредственное использование результатов вычисления составляющих напряжения по алгебраическим выражениям в балансе напряжений в узле подключения ПСТАТКОМа приводит к вычислительной неустойчивости, поэтому значения, участвующие в вычислительном процессе, определяются с помощью передаточных функций:
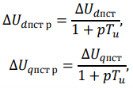
где Tu — постоянная времени, определяющая запаздывание реакции ПСТАТКОМа на изменение управляющего воздействия по каналу регулирования ЭДС, обычное значение Ti = 0,0033…0,01 с.
Разработаннаямодельсоответствуетработе ПСТАТКОМа в режиме «продольной компенсации», то есть вводимое ПСТАТКОМом напряжение всегда ортогонально вектору тока линии. Дальнейшее усложнение модели должно заключаться во включении в выражения оператора поворота вектора ΔIm на заданный угол регулирования ρ.
Заключение
В основу разработанных методов математического моделирования положено воспроизведение внешних характеристик рассматриваемых устройств FACTS.
Разработана методика расчета характеристик мощности электропередачи с компенсирующими устройствами типа СТАТКОМ и ОРПМ для сравнения эффективности влияния устройств FACTS на режимы работы энергосистем. В методике учтены ограничения по режиму напряжения в точке подключения устройства к сети и ограничения тока преобразователя СТАТКОМа (ОРПМ) при изменении угла δ.
Разработаны математические модели двух основных устройств FACTS — СТАТКОМа и ОРПМ (в составе СТАТКОМа и ПСТАТКОМа). Модели могут использоваться в составе любого программного комплекса, предназначенного для расчетов электромеханических переходных процессов.
Литература:
- Александров Г. Н. Передача электрической энергии переменным током. — М.:3нак, 1998.-272 с.
- Важнов А. И. Переходные процессы в машинах переменного тока. // -Л.: Энергия, — 1980. — С.170.
- Веников В. А., Рыжов Ю. П. Дальние электропередачи переменного и постоянного тока: Учебное пособие для вузов. — М.: Энергоатомиздат, 1985.-272 с.: ил.
- Воропай Н. И., Этингов П. В. «Координированное противоаврийное управление нагрузкой и устройствами FACTS» Электричество № 10 2005, стр. 25–37.
- Голов В. П., Мартиросян А. А., Москвин И. А., Кормилицын Д. Н. Использование управляемых электропередач с регулируемой продольной компенсацией для реализации адаптивных сетей // ЭЛЕКТРОТЕХНИКА № 2, 2017.
- Андерсон П., Фуад А. Управление энергосистемами и устойчивость / Пер. с англ. Под ред. Я. Н. Лугинского. — М.: Энергия, 1980. — 568 с.: ил.
- Грюнбаум Р, Уллерюд Ю, «FACTS: новейшее средство увеличения пропускной способности». Гибкость сети. АББ Ревю 4/2005, стр 21–24.
- Дементьев Ю. А. Применение управляемых статических компенсирующих устройств в электрических сетях // Электричество.- 2003. № 9. с.2–11.
- Дементьев Ю. А. и др. Применение статических компенсаторов для регулирования напряжения на подстанциях 330 и 500 кВ // Электрические станции, 2003, № 5.
- Демирчян К. С., Нейман Л. Р., Коровкин Н. В., Чечурин В. Л. Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 1. — 4-е изд. — СПб.: Питер, 2003.- 463 с.:ил.







