Эвристический алгоритм разбиения многосвязного ортогонального полигона с минимизацией протяженности стыков



Предложен эвристический алгоритм для приближенного решения задачи разбиения многосвязного ортогонального полигона на произвольные прямоугольные области. Критерием оптимизации служит минимизация суммарной протяженности стыков между прямоугольными областями. Рассмотрена декомпозиция задачи на две составляющие: представление исходных данных в виде графа и нахождение искомого разбиения. Описаны методы решения.

Ключевые слова: многосвязный ортогональный полигон, разбиение полигона, минимизация протяженности стыков, эвристический алгоритм

Введение

Задачи разбиения многосвязных ортогональных областей имеют важное значение в материалоемких отраслях. Такие задачи часто встречаются в строительной и судостроительной индустриях, а также в промышленности. И довольно часто задачи подобного типа решаются вручную, очевидно, что этот способ является неэффективным и приводит к большим издержкам. На данный момент для решения задачи разбиения многосвязного ортогонального полигона (МОП) на произвольные прямоугольные области с минимизацией протяженности стыков между ними отсутствуют какие-либо точные методы решения для данной задачи. Эвристики для данного критерия оптимизации также плохо изучены. Так как задача является частным случаем задач из класса геометрического покрытия, то соответственно так же имеет экспоненциальную сложность при полном переборе решений, и, следовательно, также относится к классу NP-трудных задач [1]. Как известно, для решения NP-трудных задач рациональным подходом к решению является разработка быстрых эвристических алгоритмов.

Большое количество задач можно свести к теории графов и такой подход может очень эффективно применяться на практике, так как алгоритмы на графах очень хорошо изучены и активно изучаются по сей день. Поэтому в данной статье предлагается поиск рационального решения рассматриваемой задачи с использованием алгоритмов из теории графов.

Постановка задачи разбиения многосвязного ортогонального полигона

Изначально задан многосвязный ортогональный полигон с препятствиями P. Опишем вокруг P прямоугольную область. Получим прямоугольник с шириной W и длиной L (рис. 1).

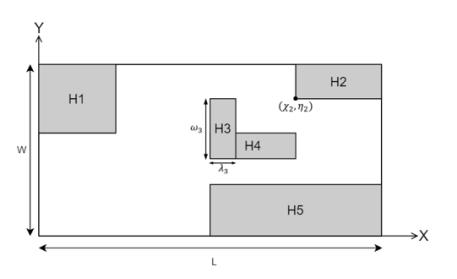
Рис.1. Пример МОП с препятствиями

При этом внутри полученного прямоугольника может образоваться множество многоугольных областей, которые не принадлежат исходному полигону P, это множество добавим ко множеству препятствий исходного полигона P. После чего все препятствия полигона разделим на прямоугольники, а так как препятствия — это односвязные ортогональные многоугольники, то для этого достаточно провести по одному отрезку в любом направлении из каждого угла внутренней области препятствия, который образует угол в 270 градусов.

Теперь введем прямоугольную систему координат, таким образом, чтобы ось OY совпадала с левой стороной прямоугольника, а ось OX — с нижней стороной. Таким образом, получаем МОП P, который можно описать следующим образом:

1) определяют соответственно длину и ширину минимально возможного прямоугольника , описывающего полигон .

2) Прямоугольные области внутри , не принадлежащие полигону , относятся к множеству препятствий , которые описываются координатами левого нижнего угла , длиной и шириной , , где — общее количество препятствий.

Пусть

− — описывает прямоугольную область, где — это координаты левого нижнего угла, — длина и ширина прямоугольника соответственно.

Требуется найти множество прямоугольных областей такое, что:

− — прямоугольные области в совокупности дают исходный полигон;

− прямоугольные области не пересекаются между собой;

− — прямоугольные области не пересекаются с препятствиями полигона;

− — это периметр исходного МОП. Т. е. суммарная протяженность стыков должна быть минимальной (рис. 2).

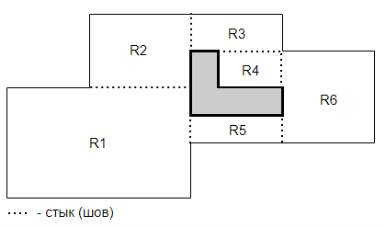
Рис. 2. Пример разбиения МОП на прямоугольники с минимальной протяженностью стыков

Алгоритм поиска рационального разбиения многосвязного ортогонального полигона

Для решения данной задачи предлагается алгоритм, использующий эвристический подход и теорию графов. Но для начала введем некоторые основные понятия. Углы во внутренней области полигона назовем вершинами полигона. Если такая вершина образует угол в 270 градусов, то она называется вогнутой, иначе — выпуклой. Две вершины являются соседями по отношению друг к другу — если они лежат на одной прямой, которая не пересекается с препятствиями полигона и параллельна одной из осей координат. Диагональ в полигоне — это отрезок, соединяющий двух соседей этого полигона.

Идея предлагаемого эвристического алгоритма состоит в том, чтобы сначала получить множество всех диагоналей исходного полигона и затем найти максимальное множество непересекающихся между собой диагоналей, которое даст некоторое начальное разбиение полигона на многоугольные области. Отметим, что таких множеств диагоналей может быть несколько, а учитывая критерий оптимизации поставленной задачи, есть смысл взять множество с минимальной суммарной длинной всех диагоналей. Далее останется сделать разбиения в получившихся многоугольных областях методом поиска кратчайшего отрезка из оставшихся свободных вогнутых вершин полигона.

Таким образом, обобщенный алгоритм решения можно разбить на следующие подзадачи:

1) Поиск максимального множества непересекающихся между собой диагоналей полигона с минимальной суммарной протяженностью. На данном шаге мы еще не имеем итоговое разбиение на прямоугольники, т. к. в результате данного этапа могут получиться многоугольники, а нам требуются прямоугольники.

2) Построение итогового разбиения полигона путем поиска кратчайших отрезков из оставшихся вогнутых вершин полигона.

1. Поиск максимального множества непересекающихся между собой диагоналей полигона. Пересечения всех диагоналей полигона можно представить в виде неориентированного графа G = , где V — множество вершин, а E — множество ребер. Вершинами в графе будут являться диагонали. Две вершины соединяются ребром, если диагонали, которые сопоставляются с этими вершинами пересекаются между собой. Полученный граф будем называть графом пересечений. Таким образом, данная задача сводится к решению задачи о независимом множестве вершин графа максимального размера. Множество вершин графа будет называться независимым, если никакие две вершины из этого множества не соединены ребром. Т. е., переводя это на нашу задачу, получим максимальное множество диагоналей, которые не пересекаются между собой. Для графов в общем случае, задача о независимом множестве является NP-трудной, однако, согласно теореме Кенига, в случае двудольных графов, она эквивалентна задаче поиска наибольшего паросочетания — это наибольшее множество ребер, таких, что никакие два ребра не имеют общей вершины, которая может быть решена за полиномиальное время. Заметим, что наш граф пересечений всегда будет являться двудольным, т. е. его вершины разбиваются на два множества так, что каждое ребро графа соединяет две вершины из разных множеств, в нашем случае два множества вершин — это вертикальные и горизонтальные диагонали.

Теперь рассмотрим подробнее, каким образом с помощью теоремы Кенига задача о независимом множестве вершин графа сводится к задаче поиска наибольшего паросочетания. Теорема Кенига утверждает, что в любом двудольном графе число ребер в наибольшем паросочетании будет равно числу вершин в наименьшем вершинном покрытии. Наименьшее вершинное покрытие графа — это наименьшее множество вершин графа, такое, что любое ребро графа имеет хотя бы одну конечную вершину из этого множества. Дополнение множества вершинного покрытия для любого графа — это независимое множество. А описанная выше эквивалентность между паросочетаниями и покрытиями, из утверждения теоремы Кенига, позволяет найти наименьшее вершинное покрытие и максимальное независимое множество графа по заданному наибольшему паросочетанию за полиномиальное время для двудольных графов, несмотря на NP-полноту этой задачи для остальных семейств графов.

Итак, для того чтобы найти максимальное множество непересекающихся между собой диагоналей полигона необходимо найти максимальное независимое множество в графе пересечений, а для этого нужно найти наибольшее паросочетание в графе и затем найти максимальное независимое множество.

1.1 Поиск наибольшего паросочетания. Все известные на данный момент алгоритмы поиска наибольшего паросочетания в двудольных графах начинают с какого-то произвольного паросочетания (необязательно максимального) и получают паросочетание большей мощности, при его существовании, с помощью выделения увеличивающего пути (определение будет дано ниже). Сложность таких алгоритмов составляет O(n³), где n — это количество вершин в графе. Однако математики Хопкрофт и Карп показали, что если дополнение осуществляется вдоль кратчайшего пути, то решение можно найти за [2]. В данный момент алгоритм Хопкрофта-Карпа является наилучшим алгоритмом нахождения наибольшего паросочетания в двудольных графах [3]. Поэтому будем использовать их алгоритм для нахождения наибольшего паросочетания в нашем двудольном графе пересечений. При этом у графа может быть несколько множеств наибольших паросочетаний и из них мы возьмем то, у которого суммарная протяженность диагоналей будет минимальной.

Алгоритм Хопкрофта-Карпа:

Пусть U, V — множества вершин двудольного графа G, а E — множество его ребер. M — паросочетание графа. Тогда вершина, которая не является концом какого-либо ребра из M, называется свободной вершиной для этого паросочетания. В алгоритме используется понятие увеличивающего пути — это путь в графе, который начинается и заканчивается в свободной вершине, а внутри пути рёбра, которые принадлежат и не принадлежат паросочетанию M чередуются между собой. Тогда если M — это паросочетание, а P — увеличивающий путь в M, то симметрическая разность двух множеств M и P является паросочетанием размера |M| + 1. Таким образом, находя увеличивающие пути, пока это возможно, можно увеличивать размер паросочетания.

Работа алгоритма начинается с пустого паросочетания M. Затем алгоритм последовательно его увеличивает, делая на каждом этапе следующие шаги:

− Поиск в ширину (ПШ) делит вершины графа на слои. ПШ начинается с множества свободных вершин U, которые образуют первый слой разбиения. Т. е. изначально первый слой полностью состоит из свободных вершин. На последующих уровнях поиска алгоритм добавляет вершины на новый уровень чередуя рёбра, добавляя то вершины из паросочетания, то не из него. ПШ прервется на уровне k, как только будет достигнута свободная вершина из множества V.

− Все свободные вершины из V на этом слое k обозначаются как F. Вершина v принадлежит F тогда и только тогда, когда в ней заканчивается кратчайший удлиняющий путь.

− Поиском в глубину находится максимальное множество, непересекающихся по вершинам, путей длины k.

− Каждый найденный путь используется для увеличения M.

Алгоритм заканчивает работу, когда на очередном шаге множество F пустое.

1.2 Поиск максимального независимого множества по заданному наибольшему паросочетанию. Как уже было сказано выше, это можно сделать по теореме Кенига, а именно применяя схему построения, которая используется для доказательства этой теоремы. Для удобства назовем эту схему алгоритмом Кенига.

Алгоритм Кенига:

Пусть М — наибольшее паросочетание двудольного графа G. Разделим вершины V графа G на подмножества S_i по следующему принципу:

− Пусть подмножество S₀ состоит из всех вершин, которые не принадлежат паросочетанию M.

− Для каждого целого , S_{2j+1 —} это множество всех вершин v, таких, что:

1. v связана с некоторой вершиной из S_2j ребром из множества E \ M
2. v не входит ни в одно из ранее построенных подмножеств S_k, для каждого k < 2j + 1.

(Если таких вершин нет, но всё еще остались вершины, которые не содержатся в ранее построенных множествах S_k, то выбираем произвольную из них и считаем, что S_2j+1 состоит из одной этой вершины).

− Для каждого целого, S_2j — это множестве всех вершин u, таких, что u принадлежит некоторому ребру из M со второй вершиной на конце из множества S_2j-1.

Согласно [4], любое ребро из M будет иметь в точности одну вершину в нечетном множестве и любое ребро из E \ M будет иметь по меньшей мере одну конечную вершину в нечетном множестве. Таким образом, объединение всех нечетных множеств даст минимальное вершинное покрытия графа с |M| вершинами, а объединение всех четных множеств даст в результате максимальное независимое множество с |E| — |M| вершинами.

2. Построение итогового разбиения полигона методом поиска кратчайших отрезков.

Пусть S — множество многоугольных областей, полученных после нахождения максимального независимого множества непересекающихся между собой диагоналей полигона, R — итоговое множество прямоугольников (изначально пустое). Работа данного этапа заключается в следующих шагах:

1. Из S берется многоугольная область s и удаляется из данного множества.
2. Если s — прямоугольник, то s добавляется в R и осуществляется переход к шагу 1.
3. Из s берется произвольная вогнутая вершина и из неё проводится отрезок до ближайшего по расстоянию ребра s. Область s при этом будет разделена на две многоугольные области s1 и s2, которые добавляются во множество S и осуществляется переход к шагу 1.

Шаги алгоритма повторяются до тех пор, пока множество S не пустое. Полученное множество R будет разбиением исходного многосвязного ортогонального полигона на прямоугольные области с приближенной к минимальной протяженности стыкам между ними.

Литература:

1. Lingas, Pinter, Rivest and Shamir. Minimum Edge Length Partitioning of Rectilinear Polygons (1982)
2. Свами М., Тхуласираман К. Графы, сети и алгоритмы (1984)
3. Hopcroft, John E. and Karp, Richard M. An n 5/2 algorithm for maximum matchings in bipartite graphs. SIAM Journal on Computing (1973)
4. Bondy J. A., Murty U. S. R. Graph Theory with Applications. North Holland, ISBN 0–444–19451–7 (1976)