Своё начало история логарифмов берёт ещё с античных времён. Источник, ставший идейным толчком применения логарифмов, — давно известный факт, что при перемножении степеней с одинаковым основанием их показатели складываются: 
.
В VIII веке индийский математик Вирасена при исследовании степенных зависимостей, опубликовал таблицу целочисленных показателей для оснований 2, 3, 4. Эта работа в дальнейшем послужила первоисточником для создания таблицы логарифмов.
Главные работы и открытия в области изучения логарифмов были сделаны в средневековой Европе. В тот период времени быстро возросла потребность в сложных расчётах. В XVI веке большая часть трудностей в вычислениях была связана с умножением и делением многозначных чисел, возведением в степень, а также извлечением корней. Идея упрощения вычислений появилась в конце века. Её суть состояла в замене трудоёмкого умножения на простое сложение. Идея основывалась на сопоставлении геометрической и арифметической прогрессий с помощью специальных таблиц, причём геометрическая прогрессия являлась исходной. Соответственно, и деление заменилось на более простое вычитание. Также упростилась работа со степенью и извлечением корня.
Такой метод вычислений впервые был опубликован в 1544 году в книге «Arithmetica integra» Михаэлем Штифелем. К сожалению, ему не удалось найти практической реализации своей идее, т. к. математика в те времена была не столь развита и идея логарифма не нашла своего развития. Да и сам Штифель не приложил серьёзных усилий для этого. Главная заслуга математика — переход от целых показателей степени к произвольным рациональным.
В 1614 году шотландским математиком Джоном Непером было опубликовано сочинение на латинском языке под названием «Описание удивительной таблицы логарифмов». В своей работе ему удалось раскрыть идею логарифма числа как показателя степени, в которую нужно возвести данное основание, чтобы получить это число. Он перенес знакомые свойства прогрессии с общим членом на любые действительные показатели. Это дало непрерывную логарифмическую функцию.
В сочинении Непера было дано краткое описание логарифмов и их свойств и опубликованы 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1'. Термин логарифм, который был предложен Непером, утвердился в науке. В другой книге Непера «Построение удивительной таблицы логарифмов», более подробно описана теория логарифмов. Книга была издана в 1619 году его сыном Робертом уже после смерти учёного.
Анализ документов, изучение сочинений говорят о том, что техникой логарифмирования Непер владел уже к 1594 году. В связи с развитием изучения небесных тел, появилась необходимость в облегчении сложных астрономических расчётов. Именно поэтому в таблицы были включены только логарифмы тригонометрических функций.
В то время понятия функции ещё не существовало, и Непер кинематически определил логарифм, сопоставляя равномерное и логарифмически-замедленное движение. К примеру, логарифм синуса был определен так:
«Логарифм данного синуса есть число, которое арифметически возрастало всегда с той же скоростью, с какой полный синус начал геометрически убывать» [1].
В истории математики зародилось такое понятие как «Логарифм Непера» (обозначается LogNap). Основное его свойство звучит так: «Если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую». Но правила логарифмирования отличались от современных.
Одновременно с Непером изучением логарифмов занимался английский математик Генри Бригс. В 1617 году он опубликовал первый свой труд — таблицу, в которой содержались 14-значные десятичные логарифмы от 1 до 1000. — «Первую тысячу логарифмов» в год смерти Непера. Здесь даны были десятичные логарифмы чисел от 1 до 1000 с четырнадцатью знаками. Позднее, Бригсом была выпущена «Логарифмическая арифметика», в которой содержались 14-значные таблицы логарифмов целых чисел от 1 до 20 000 и от 90 000 до 100 000.
В 1703 году были изданы первые таблицы на русском языке при участии русского математика Леонтия Филипповича Магницкого. Активно теорию логарифмов развивал петербургский академик Леонард Эйлер. Именно он впервые стал рассматривать логарифмирование как действие, которое обратно возведению в степень. Также им введены в употребление в термины «основание логарифма» и «мантисса».
В истории математики описывается и другой подход к определению логарифма. Учёные-математики рассматривали его как площадь криволинейной трапеции. Данный подход основывается на рассмотрении связи натурального логарифма 
с гиперболой. Григорий Сен Венсан во второй трети 17 века показал, что если абсциссы любых двух точек А и В на гиперболе 
соответственно пропорциональны абсциссам точек А1 и В2 на той же кривой, то площади криволинейных четырехугольников, расположенных под отрезками гиперболы АВ и А1В1, равны [4]. Такое предложение определило развитие следующего равенства: , где 
. По этой формуле вычислялась площадь под данной гиперболой, и она равнялась , чему соответствует рисунок 1.
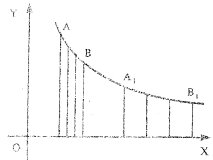
Рис. 1. Связь гиперболы и площади криволинейной трапеции
Такую связь выразил в форме бесконечного ряда и опубликовал около 1657г. в статье «Квадратура гиперболы с помощью бесконечного ряда рациональных чисел» Уильям Броункер. Ряд таких чисел выглядел следующим образом:
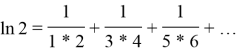
Ранее данное разложение опубликовал итальянский математик Пьетро Менголи. В «Новых арифметических квадратурах или о сложении дробей» учёным были просуммированы некоторые числовые ряды:
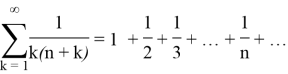
Им же была доказана расходимость гармонического ряда 
путём применения неравенства:
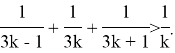
Эту работу он применил к изучению логарифмов [2, c. 160]. Но труды Менголи не привлекли должного внимания большинства современников. Отчасти, работы не получили широкого применения из-за трудности изложения материала.
Возникновение аналитического аппарата бесконечно малых в конце 17в. определило следующий подход к изучению логарифма. Путём представления логарифмической функции в форме бесконечного степенного ряда было получено её аналитическое представление:
[3, c.44].
В 1711 году Исаак Ньютон в сочинении «Анализ с помощью уравнений с бесконечным числом членов» применил методы неопределенных коэффициентов и последовательных приближений. Именно ему удалось получить аналитическое выражение показательной функции:
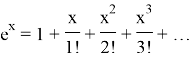
и дать трактовку показательной функции как обратной к логарифмической.
Важный шаг в исследовании логарифмической функции сделал Николай Кауфман (более известный как Меркатор). Он представил логарифмическую функцию в форме бесконечного степенного ряда. Почти одновременно с появлением статьи Броункера был опубликован труд Меркатора в «Логарифмотехнике», посвященный изучению логарифмов. Перейдя от равносторонней гиперболы , он применил к дроби 
деление по правилам алгебры, которое, в данном случае, продолжается без конца
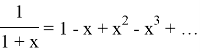
и путём почленного интегрирования он нашёл связь натурального логарифма с данной дробью:
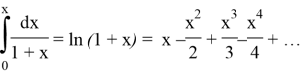
Меркатор не первый пришел к разложению логарифмической функции в степенной ряд. К такому же результату пришли Гудде в 1656г. и Ньютон в 1665г., но каждый из них хранил свой труд, не опубликовав его. Именно поэтому значение публикации «Логарифмотехника» оказалось очень велико.
История изучения логарифмов и логарифмической функции подчеркивает неразрывную связь отдельных областей математики — алгебры, геометрии, математического анализа. Логарифм стал великим открытием, значимым для математики и дал толчок развитию математического образования.
Литература:
- История логарифмов [Электронный ресурс]/ Википедия — интернет-энциклопедия. Режим доступа: https://ru.wikipedia.org — свободный. Дата обращения: 27.03.2019г.
- История математики с древнейших времен до начала XIX столетия/ Под ред. А. П. Юшкевича М.: Наука, 1972. Т.II. 300 с.; Т. III. 495 с.
- Прокина-Игнатушина И. В. Об истории возникновения понятия логарифмической функции// Научные труды молодых ученых ОГПУ. Оренбург: ОГПУ, 2000. С. 43–49.
- Различные подходы к определению логарифма и логарифмической функции [Электронный ресурс]/ Инфоурок — образовательный портал. Режим доступа: https://infourok.ru — свободный. Дата обращения: 25.03.2019г.
