В статье описаны условия и качества знаний, оказывающие влияние на прочность знаний, а также показатели, с помощью которых можно проверить прочность знаний учащихся. Предложена методика повышения прочности знаний, основанная на использовании коммуникативных задач, и проведена проверка ее эффективности.
Ключевые слова: коммуникативная задача, осознанность знаний, прочность знаний, система качеств знаний.
В обучении принцип прочности знаний рассматривается как один из основополагающих. Особенно важным является формирование прочных знаний в процессе обучения математике (в частности, геометрии). Это связано с особенностью содержания предмета в общеобразовательной школе. Данная особенность состоит в жесткой связи разделов курса, предыдущие знания являются основой для построения последующих, поэтому от того, насколько прочно усвоены предшествующие знания, зависит усвоение последующих. Достижение прочного усвоения материала учащимися остается одной из главных проблем в методике обучения на протяжении многих лет. Поиск возможных путей повышения прочности знаний учащихся привел к использованию на уроках коммуникативных задач, так как со стороны учащихся был отмечен повышенный интерес к задачам, решение которых можно обсуждать с учеником-партнером. Все вышесказанное в целом актуализирует проблему повышения прочности знаний учащихся и показывает, что ее решение приведет к получению большего количества выпускников с качественными, прочными знаниями.
Цель статьи состоит в том, чтобы рассмотреть основные аспекты данной проблемы и проверить эффективность методики повышения прочности знаний при обучении геометрии, основанной на использовании такого средства как коммуникативные задачи.
Условия и показатели формирования прочных знаний. И. Я. Лернер рассматривал знания, как результат общественного познания и выделял следующие качества знаний, которые все вместе образуют систему качеств знаний:
– полнота и глубина;
– оперативность и гибкость;
– систематичность и системность;
– осознанность и прочность;
– конкретность и обобщенность;
– свернутость и развернутость [5, стр.38].
Педагогика рассматривает личностные знания учащегося, которые формируются постепенно: одни раньше, другие позже. Таким образом, часть качеств знаний формируются уже на первом уровне усвоения, а часть только на втором и третьем[1]. Следовательно, если учащийся не смог освоить все три уровня усвоения материала, то он не может обладать всей системой качеств знаний, а только частью из них. В первую очередь знания обретают конкретность, затем определенную степень полноты, оперативности и систематичности. В зависимости от системы обучения и конкретного учащегося постепенно могут формироваться и другие качества, но не обязательно. Достижение учащимися определенного набора качеств имеет прямое отношение к формированию одного из самых важных качеств знаний — прочности. «Прочность состоит в устойчивой фиксации в памяти системы существенных знаний и способов их применения или в готовности вывести необходимые знания, основываясь на других опорных знаниях» [5, стр.38].
В современном мире при обучении нужно стараться организовывать учебный процесс таким образом, чтобы добиваться прочности знаний за счет осознанности учащимися полученных знаний (учитывая также и психофизиологическую особенность памяти учащихся). Таким образом, необходимое условие получения прочно усвоенных знаний — их осознанность.
Как показал анализ литературы, про осознанность можно сказать, что она является базовым качеством знаний: все остальные качества знаний связаны с ней. Для одних качеств знаний осознанность является средством их проявления, для других — средством формирования. Среди набора качеств знаний есть несколько, оказывающих влияние на формирование осознанности знаний учащихся:
– определенная степень полноты и систематичности, поскольку они касаются связей между знаниями;
– оперативность, поскольку применение знаний при решении различных задач или ситуаций помогает осознанному усвоению знаний.
Для формирования и совершенствования систематичности знаний в геометрии полезно давать учащимся задания на самостоятельное установление связей между объектами. Например, при объяснении темы «ромб» или «квадрат» попросить их определить связь данных объектов с другими четырехугольниками и подумать, частными случаями каких четырехугольников они могут являться.
Для формирования и совершенствования оперативности знаний необходимо, чтобы учащиеся старались увидеть несколько способов решения каждой задачи. Для этого регулярно нужно предлагать учащимся решить задачу несколькими способами.
Ряд педагогов (Л. Я. Зорина, И. П. Подласый, С. Л. Рубинштейн и др.) считает, что существенным условием для получения прочно усвоенных знаний является положительное эмоциональное отношениекизучаемому материалу и учебной деятельности в целом. Следовательно, память учащихся имеет избирательный характер: чем значимее и интереснее для них учебный материал, тем прочнее этот материал фиксируется в памяти.
При создании методики, направленной на получение учащимися прочно усвоенных знаний, необходимо учитывать психофизиологическую особенность памяти учащихся. Частота и время повторений должны быть связаны с кривой забывания. Герман Эббингауз установил, что процессы запоминания и забывания имеют нелинейный характер. Рассмотрим особенности кривой забывания: она показывает, что в течение первого часа после безошибочного повторения материала забывается более 50 % данных. Следовательно, большая часть материала забывается в первые минуты после обучения, гораздо меньше в ближайшие дни [8].
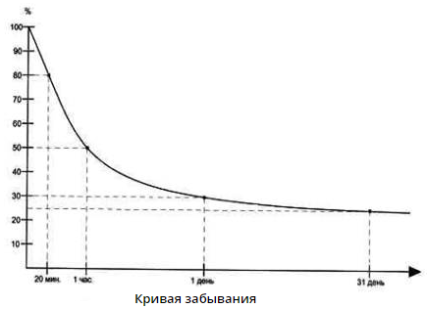
Учитывая данные особенности памяти, предлагаем организовать учебный процесс, используя следующий график повторения Эббингауза для длительного запоминания:
|
Номер повторения |
Рекомендуемый срок повторения |
|
I |
сразу же после изучения материала |
|
II |
через 20–30 минут |
|
III |
через сутки |
|
IV |
через 2–3 недели |
|
V |
через 2–3 месяца |
|
VI |
Через 2 года |
Если мы говорим о показателях формирования прочных знаний, то мы имеем в виду способ, с помощью которого можно проверить, прочно усвоены те или иные знания учащимися или нет. Проведя анализ литературы, было выявлено, что осознанность является не только условием получения прочных знаний, но и первым показателем прочности усвоения знаний.Если учащийся не в состоянии осознать полученное знание, то вероятность того, что «зазубривание» поможет запомнить его на длительный срок, крайне мала.
Второй показатель прочности знаний — это способность ученика, используя знания, служащие в данном случае опорными, восстанавливать в памяти другие знания. Полученные знания далеко не всегда сохраняются в памяти на длительный срок. Это в первую очередь связано с перенасыщением нашего мозга огромным количеством информации каждый день. Следовательно, способность восстанавливать в памяти одни знания, опираясь на другие, является очень важной. В качестве примера можно привести задачу, в которой ученику нужно найти градусную меру всех углов ромба ABCD, при этом известна градусная мера угла A. В данной задаче ученику нужно помнить, что ромб — это частный случай параллелограмма. Противоположные углы параллелограмма равны — а значит и у нашего ромба противоположные углы также равны. Получается, что ученику не надо отдельно запоминать, что у ромба противоположные углы равны: это можно вывести на основе опорных знаний о том, что ромб — это частный случай параллелограмма, а значит все свойства, которые работают для параллелограмма, работают и для ромба.
Систематизируем все вышеизложенное и представим его в виде схемы.
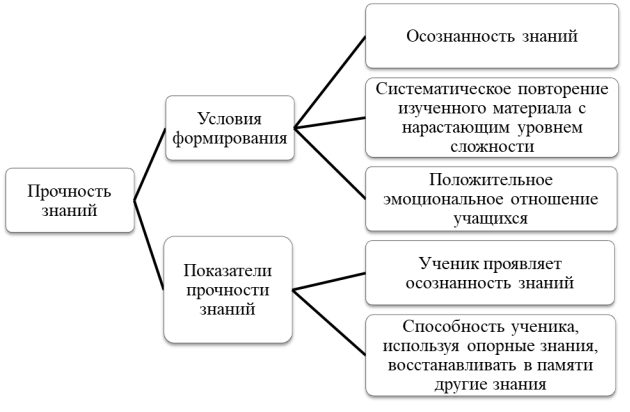
Понятие коммуникативной задачи. Рассмотрим понятие «коммуникативная задача» и её соотношение с познавательной. Как отмечает автор системного анализа задач Г. А. Балл, структура предмета этих задач аналогична, а предметом этих двух видов задач является знание, нуждающееся в усовершенствовании [4, с.87]. Значит, когда мы говорим о коммуникативных задачах, мы имеем в виду познавательные задачи, которые решаются совместно учениками-партнерами. Например, ученик I умеет решать определенную задачу (боковые стороны трапеции, описанной около окружности, равны 3 и 5, найдите среднюю линию трапеции), тогда его коммуникативная задача будет состоять в том, чтобы объяснить ученику II, как можно решить эту задачу (рассказать ему о свойстве четырехугольника, описанного около окружности и том, как найти среднюю линию трапеции). При этом решая свою коммуникативную задачу (научить решать данную задачу ученика II) ученик I предлагает решить познавательную задачу ученику II. Если ученик II поймет, как решать такую задачу, то можно сказать, что ученик I решил свою коммуникативную задачу (научить ученика II решать данную задачу).
Насыщение деятельности учащихся коммуникативными задачами повышает мотивационную составляющую и результативность обучения. Например, в экспериментах В. В. Андриевской [3] ученики должны были вычленить смысловую структуру сюжетного рисунка (мыслительная задача) и описать эту структуру понятно для ученика-партнера (коммуникативная задача). Было установлено, что при выполнении коммуникативной задачи ученики прилагали больше усилий, чем при выполнении познавательной задачи (ранее в эксперименте предлагалось подобное задание по картинкам, только не нужно было описывать структуру рисунка другому ученику), они пытались выработать эффективную стратегию анализа изображений, чтобы быстрее и понятнее объяснять информацию ученику-партнеру.
Методика, направленная на получение учащимися прочных знаний. Для развития качеств знаний, оказывающих влияние на прочность, достаточно решения коммуникативных задач обучающего и поискового уровня. В современных учебниках по геометрии крайне мало таких познавательных задач. Чтобы иметь возможность отличать познавательные задачи друг от друга (и от других задач), рекомендуем использовать типологию познавательных задач, разработанную О. А. Абдулаевой [1,2].
Познавательные задачи (обучающий и поисковый уровень)
|
Обучающие задачи |
Задачи, в которых неизвестен (или плохо определен) один из основных компонентов структуры задачи |
хТОР |
Алгоритмический уровень (интерпретирующий уровень) |
|
УТхР | |||
|
УТОх | |||
|
Поисковые задачи |
Неизвестны какие-либо два компонента структуры задачи |
ххОР |
Творческий (поисковый уровень) |
|
УххР | |||
|
УТхх | |||
|
хТхР | |||
|
хТОх | |||
|
УхОх |
В данной таблице приняты следующие обозначения:
У — условие задачи;
Т — требование задачи;
О — обоснование решения;
Р — решение задачи;
x — неизвестные компоненты структуры задачи.
Для достижения цели данного исследования на уроках будет организовано решение коммуникативных задач по следующей схеме:
- Решение поисковых задач на уроке в парах/группе (учитель направляет и корректирует деятельность учащихся).
- Раз в неделю в качестве домашнего задания будут выдаваться две обучающие задачи на пару (ученики-партнеры, сидящие за одной партой). Ученик I дома разбирает первую полученную задачу таким образом, чтобы на следующем уроке в классе смочь доступно объяснить решение данной задачи ученику II (ученику-партнеру). Аналогично работает дома ученик II. В начале следующего урока для объяснения своих задач ученику-партнеру будет выделено 6–8 минут (в зависимости от уровня класса). Затем каждый учащийся письменно должен решить задачу, подобную одной из двух заданных на дом.
Проверка эффективности разработанной методики производилась путем проведения опытно-экспериментальной работы, котораяпроходила в два этапа: констатирующий и обучающий.
Констатирующий этап опытно-экспериментальной работы включал проверку того, насколько прочно были сформированы знания по геометрии учащихся 8 классов. В диагностической работе учащимся предлагалось решить 6 задач по геометрии, которые учащиеся уже решали ранее (за 2–6 месяцев до проведения эксперимента). Анализ выполненных работ показал, что учащиеся смогли решить только 36 % того, что они решали ранее. Таким образом, рабочая гипотеза констатирующего эксперимента подтвердилась — современные учащиеся не обладают достаточной прочностью знаний.
Основная цель обучающего этапа опытно-экспериментальной работы состояла в том, чтобы проверить эффективность методики, основанной на использовании при обучении коммуникативных задач. До проведения обучающего эксперимента была проведена подготовительная работа:
– были отобраны познавательные задачи обучающего и поискового уровня;
– разработана методика работы с данными задачами на уроках геометрии.
Эксперимент проводился в школе № 559 Выборгского района г. Санкт-Петербурга. Всего в эксперименте приняло участие 53 учащихся 8 класса. На протяжении двух месяцев проводились уроки с использованием коммуникативных задач в экспериментальной группе (ноябрь и март) и познавательных задач в контрольной группе. В мае (т. е. через 2–6 месяцев после работы с данными задачами) была предложена диагностическая работа для проверки прочности знаний учащихся обеих групп.
Результаты экспериментальной группы
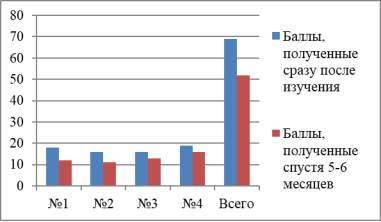
Результаты контрольной группы
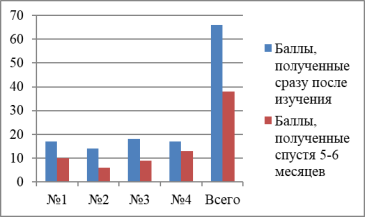
Анализ диаграмм показывает, что у учащихся экспериментальной группы прочность знаний оказалась выше (75 %), чем у учащихся контрольной группы (58 %). Также учащиеся экспериментальной группы в целом показали лучший результат сразу после изучения материала, чем учащиеся контрольной группы (44,2 % против 40,7 %).
Заключение. Результаты обучающего эксперимента подтвердили эффективность систематического использования коммуникативных задач при обучении геометрии. Разработанная методика способствовала повышению прочности знаний учащихся. Также со стороны учащихся был отмечен повышенный интерес к задачам, решение которых можно обсуждать с учеником-партнером.
Литература:
- Абдулаева О. А. Педагогический потенциал учебно-познавательных задач: учебно-методическое пособие. — СПб.: СПб АППО, 2010. — 74 с.
- Абдулаева О. А. Учебно-познавательные задачи как способ приобщения учащихся к творческой деятельности: учебно-методическое пособие. — СПб.: СПб АППО, 2015. — 84 с.
- Андриевская В. В. Влияние регламентированного общения учащихся на их деятельность по анализу сюжетных изображений // Учебный материал и учебные ситуации. — Киев, 1986. — с. 13–20
- Балл Г. А. Теория учебных задач: Психолого-педагогический аспект. — М.: Педагогика, 1990. — 184с.
- Лернер И. Я. Качества знаний учащихся. Какими они должны быть? — М.: Знание, 1978. — 48с.
- Подласый И. П. Педагогика: 100 вопросов — 100 ответов: учебное пособие для вузов. — М.: ВЛАДОС-пресс, 2004. — 365 с.
- Рубинштейн С. Л. Проблемы общей психологии. — М.: Педагогика, 1973. — 424 с.
- Эббингауз Г. О памяти. — Lpz., 1885
[1] Существует три уровня усвоения знаний:
- первый уровень состоит в осознанном восприятии новых знаний и первичном их закреплении, т.е. выделение объекта из общей среды и встраивание информации о нем в систему знаний учащихся;
- второй уровень заключается в усвоении способов применения данных знаний в типовых задачах, включая легко опознаваемые вариации типовых задач.
- третий уровень усвоения знаний представляет собой готовность учащегося творчески применить усвоенную информацию в новой, нетиповой задаче.

