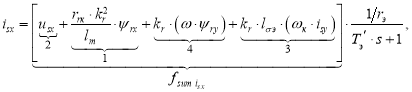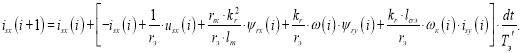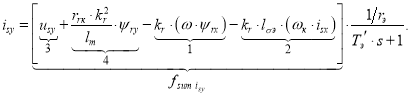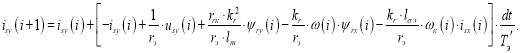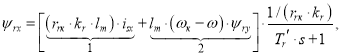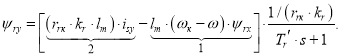В данной работе дадим сравнение математических моделей в Matlab-Simulink, Matlab-Script и Си. Причем модели в Matlab были рассмотрены ранее в журналах «Молодой ученый», начиная с 2017 г., а в Си приводим впервые.
На наш взгляд, будет правильным дать каждое уравнение в сравнении друг с другом в различных способах решения.
1. Определение статорного тока isx
Matlab-Simulink:
В работе [1] была получена структурная схема для определения статорного тока isx в Simulink по следующему уравнению, которому соответствует структурная схема (рис. 1):
|
|
(1) |
где![]() - электрическая скорость вращения ротора;
- электрическая скорость вращения ротора;
![]() - механическая угловая скорость на валу двигателя;
- механическая угловая скорость на валу двигателя;
![]() - постоянная времени статорной обмотки.
- постоянная времени статорной обмотки.
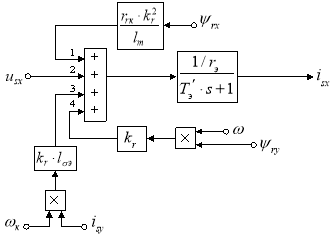
Рис. 1. Структурная схема для определения тока isx в Simulink
Matlab-Script:
Из выражения для isx (1) получим выражение в Script. Обозначим сумму в квадратных скобках через fsum isx, тогда:
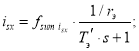
![]()
Перейдем к оригиналу, для этого оператор s заменим ![]() :
:
![]()
Оставим первую производную в левой части:
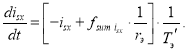
Заменим disx конечной разностью isx(i+1) isx(i):
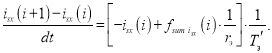
Отсюда ток isx:
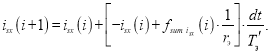
Раскрывая fsum isx(i), получим:
|
|
(1') |
Си:
Это уравнение (1’) является основой для определения isx в Си:
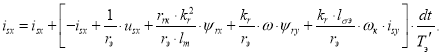
Это уравнение повторяет уравнения в Script (1’) с небольшими изменениями в виде исключения скобок с переменными i и i+1. Видимо, если циклы будут составлять несколько сотен тысяч, то это скажется на быстродействии.
2. Определение статорного тока isy
Уравнение для определения тока isy в Simulink, полученное в работе [1]:
|
|
(2) |
Структурная схема реализации уравнения (2) приведена на рис. 2.

Рис. 2. Структурная схема для определения тока isy в Simulink
Аналогично преобразуем выражение тока isy для программирования в Matlab-Script:
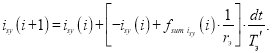
Раскрывая fsum isy(i), получим:
|
|
(2') |
Это уравнение (2’) лежит в основе для записи уравнения тока isy при программировании на языке Си:
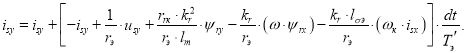
3. Определение потокосцепления ψrx
В работе [1] была получена структурная схема для определения потокосцепления ψrx в Simulink (рис. 3) по следующему уравнению:
|
|
(3) |
где![]() - постоянная времени потока.
- постоянная времени потока.

Рис. 3. Структурная схема для определения потокосцепления ψrx в Simulink
Преобразуем уравнение (3) для программирования в Matlab-Script:
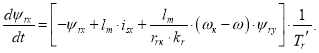
Переходим к конечным разностям:
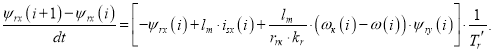
Определим потокосцепление ψrx в Matlab-Script:
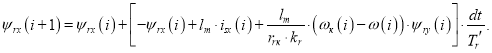
Уравнение потокосцепления ψrx для программирования на языке Си:
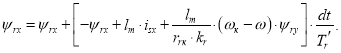
4. Определение потокосцепления ψry
Уравнение для определения потокосцепления ψry в Simulink, полученное в работе [1], имеет следующий вид:
|
|
(4) |
Структурная схема реализации уравнения (4) приведена на рис. 4.
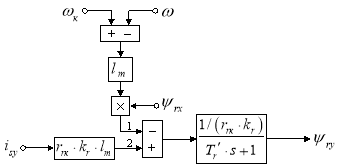
Рис. 4. Структурная схема для определения потокосцепления ψry в Simulink
Преобразуем выражение потокосцепления ψry в форму, удобную для программирования в Matlab-Script:
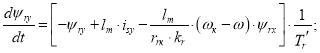
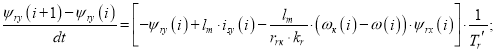
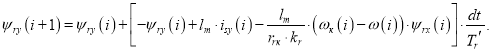
Уравнение ψry для программирования на языке Си будет иметь вид:
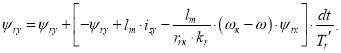
На рис. 5 представлена структурная схема для реализации уравнения электромагнитного момента в Matlab-Simulink:
![]()

Рис. 5. Математическая модель электромагнитного момента m в Simulink
Уравнение электромагнитного момента для Matlab-Script:
![]()
Уравнение электромагнитного момента для реализации на языке Си:
![]()
Механическая угловая скорость вращения вала двигателя в Simulink (рис. 6):
![]()
![]()
Рис. 6. Математическая модель определения механической угловой скорости вращения вала двигателя в Simulink
Отсюда механическая угловая скорость вращения вала двигателя в Matlab-Script:
![]()
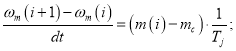
Уравнение механической угловой скорости на языке Си:
![]()
Электрическая скорость вращения ротора в Simulink (рис. 7):
![]()
![]()
Рис. 7. Математическая модель определения электрической скорости вращения ротора в Simulink
Электрическая скорость вращения ротора в Matlab-Script:
![]()
Уравнение электрической скорости на языке Си:
![]()
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными is – ψr на выходе апериодических звеньев приведена на рис. 8. Параметры асинхронного двигателя рассмотрены в работах [2] и [3].
Расчет параметров производим в Script:
|
PN=320000; |
UsN=380; |
IsN=324; |
fN=50; |
zp=3; |
|
Omega0N=104.7; |
Rs=0.0178; |
Xs=0.118; |
Xm=4.552; |
Xr=0.123; |
|
OmegaN=102.83; |
J=28; |
kd=1.0084; |
roN=0.9962; |
|
|
Ub=sqrt(2)*UsN; |
OmegasN=2*pi*fN; |
Omegab=OmegasN; |
||
|
Ib=sqrt(2)*IsN; |
Omegarb=Omegab/zp; |
Mb=kd*PN/OmegaN; |
||
|
betaN=(Omega0N-OmegaN)/Omega0N; |
Zb=Ub/Ib; |
|||
|
rrk=roN*betaN; |
lbs=Xs/Zb; |
lbr=Xr/Zb; |
lm=Xm/Zb; |
rs=Rs/Zb; |
|
kr=lm/(lm+lbr); |
lbe=lbs+lbr+lbs*lbr/lm; |
Pb=Mb*Omegarb; |
||
|
Tr=lm/(rrk*kr); |
re=rs+rrk*kr^2; |
Tj=J*Omegarb/Mb; |
||
|
Tr1=Tr/Omegab; |
Te=kr*lbe/re; |
SsN=3*UsN*IsN; |
||
|
Te1=Te/Omegab; |
ZetaN=SsN/Pb; |
|||
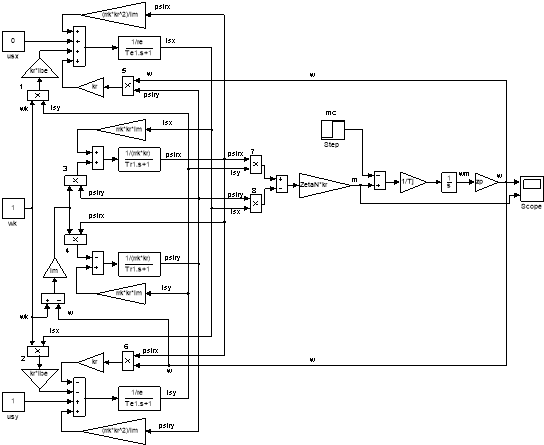
Рис. 8. Математическая модель асинхронного двигателя с переменными is – ψr на выходе апериодических звеньев в Matlab-Simulink
Результаты моделирования асинхронного двигателя в Simulink представлены на рис. 9.
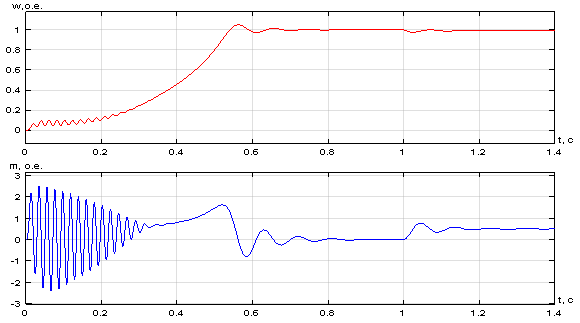
Рис. 9. Графики скорости и электромагнитного момента в Simulink
Реализация математической модели асинхронного двигателя с короткозамкнутым ротором с переменными is – ψr в Matlab-Script в системе относительных единиц приведена в листинге 1.
Листинг 1
% Номинальные данные
PN=320000; UsN=380; IsN=324; fN=50;
Omega0N=104.7; OmegaN=102.83; zp=3;
% Параметры Т-образной схемы замещения при номинальной частоте
Rs=0.0178; Xs=0.118; Xr=0.123; Xm=4.552; J=28;
% Базисные величины системы относительных единиц
Ub=sqrt(2)*UsN;
Ib=sqrt(2)*IsN;
OmegasN=2*pi*fN;
Omegab=OmegasN;
Omegarb=Omegab/zp;
Zb=Ub/Ib;
kd=1.0084;
Mb=kd*PN/OmegaN;
Pb=Mb*Omegarb;
% Расчет коэффициентов
rs=Rs/Zb;
lbs=Xs/Zb;
lbr=Xr/Zb;
lm=Xm/Zb;
Tj=J*Omegarb/Mb;
betaN=(Omega0N-OmegaN)/Omega0N;
SsN=3*UsN*IsN;
ZetaN=SsN/Pb;
kr=lm/(lm+lbr);
lbe=lbs+lbr+lbs*lbr/lm;
roN=0.9962;
rrk=roN*betaN;
Tr=lm/(rrk*kr);
Tr1=Tr/Omegab;
re=rs+rrk*kr^2;
Te=kr*lbe/re;
Te1=Te/Omegab;
% Расчет модели асинхронного двигателя
dt=0.000001; t=0; t1=1.4;
cnt=t1/dt;
for i=1:cnt
if(t>=1)
mc=0.5;
else
mc=0;
end;
wk(i)=1; usx(i)=0; usy(i)=1; isx(1)=0; isy(1)=0;
psirx(1)=0; psiry(1)=0; wm(1)=0; w(1)=0;
isx(i+1)=isx(i)+(-isx(i)+(1/re)*usx(i)+rrk*(kr^2)/ (re*lm)*psirx(i)+(kr/re)*w(i)*psiry(i)+(kr*lbe/re)*wk(i)*isy(i))*dt/Te1;
isy(i+1)=isy(i)+(-isy(i)+(1/re)*usy(i)+rrk*(kr^2)/(re*lm)*psiry(i)-(kr/re)*w(i)*psirx(i)-(kr*lbe/re)*wk(i)*isx(i))*dt/Te1;
psirx(i+1)=psirx(i)+(-psirx(i)+lm*isx(i)+(lm/(rrk*kr))*(wk(i)-w(i))*psiry(i))*dt/Tr1;
psiry(i+1)=psiry(i)+(-psiry(i)+lm*isy(i)-(lm/(rrk*kr))*(wk(i)-w(i))*psirx(i))*dt/Tr1;
m(i+1)=ZetaN*kr*(psirx(i+1)*isy(i+1)-psiry(i+1)*isx(i+1));
wm(i+1)=wm(i)+(m(i)-mc)*dt/Tj;
w(i+1)=wm(i+1)*zp;
t=t+dt;
% mass
mass_t(i)=i*dt;
mass_m(i)=m(i+1);
mass_w(i)=w(i+1);
end;
% Построение графиков
figure(1);
plot(mass_t,mass_w,'r');
grid on;
figure(2);
plot(mass_t,mass_m,'b');
grid on;
Результаты моделирования асинхронного двигателя в Matlab-Script даны на рис. 10.
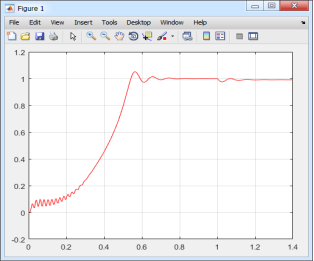
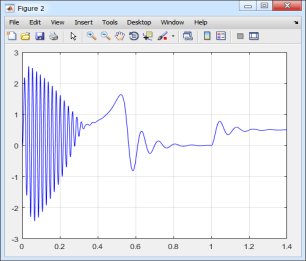
Рис. 10. Графики скорости и электромагнитного момента в Matlab-Script
Математическая модель асинхронного двигателя с переменными is – ψr на языке программирования Си дана в листинге 2.
Листинг 2
#include
#undef __STRICT_ANSI__
#include
#include "gnuplot_i.h"
#define FILENAME "tmp.txt"
int main(void) {
// номинальные данные
const double PN=320000,
UsN=380,
IsN=324,
fN=50,
Omega0N=104.7,
OmegaN=102.83,
zp=3,
// параметры Т-образной схемы замещения при номинальной частоте
Rs=0.0178,
Xs=0.118,
Xr=0.123,
Xm=4.552,
J=28,
// базисные величины системы относительных единиц
Ub=sqrt(2)*UsN,
Ib=sqrt(2)*IsN,
OmegasN=2*3.14*fN,
Omegab=OmegasN,
Omegarb=Omegab/zp,
Zb=Ub/Ib,
kd=1.0084,
Mb=kd*PN/OmegaN,
Pb=Mb*Omegarb,
// расчет коэффициентов
rs=Rs/Zb,
lbs=Xs/Zb,
lbr=Xr/Zb,
lm=Xm/Zb,
Tj=J*Omegarb/Mb,
betaN=(Omega0N-OmegaN)/Omega0N,
SsN=3*UsN*IsN,
ZetaN=SsN/Pb,
kr=lm/(lm+lbr),
lbe=lbs+lbr+lbs*lbr/lm,
roN=0.9962,
rrk=roN*betaN,
Tr=lm/(rrk*kr),
Tr1=Tr/Omegab,
re=rs+rrk*kr*kr,
Te=kr*lbe/re,
Te1=Te/Omegab;
// переменные математической модели асинхронного двигателя
double wk=1,
usx=0,
usy=1,
isx=0,
isy=0,
psirx=0,
psiry=0,
wm=0,
w=0,
m=0,
mc=0;
double dt=1e-3; // шаг интегрирования
double t=0; // текущее значение времени
double t1=1.4; // конечное значение времени расчета
unsigned int cnt=t1/dt; // количество точек
// Создаем временный файл, в который будем записывать текущие значения
FILE *fp = fopen(FILENAME, "w");
// цикл расчета
for (unsigned int i = 0; i < cnt; i++) {
// подача возмущающего воздействия
mc = (t >= 1.0f)? 0.5f: 0.0f;
// расчет мат модели асинхронного двигателя
isx=isx+(-isx+(1/re)*usx+rrk*(kr*kr)/(re*lm)*psirx+(kr/re)*w*psiry+ (kr*lbe/re)*wk*isy)*dt/Te1;
isy=isy+(-isy+(1/re)*usy+rrk*(kr*kr)/(re*lm)*psiry-(kr/re)*w*psirx-(kr*lbe/re)*wk*isx)*dt/Te1;
psirx=psirx+(-psirx+lm*isx+(lm/(rrk*kr))*(wk-w)*psiry)*dt/Tr1;
psiry=psiry+(-psiry+lm*isy-(lm/(rrk*kr))*(wk-w)*psirx)*dt/Tr1;
m=ZetaN*kr*(psirx*isy-psiry*isx);
wm=wm+(m-mc)*dt/Tj;
w=wm*zp;
// записываем точки во временный файл
fprintf(fp,"%f\t%f\t%f\n", t, m, w);
// увеличиваем переменную время
t=t+dt;
}
// Закрываем текстовый файл с текущими значениями
fclose(fp);
// Рисуем графики
gnuplot_ctrl *h;
h=gnuplot_init();
gnuplot_cmd(h, "set grid xtics ytics"); // вкл сетка
gnuplot_cmd(h, "plot '%s' u 1:2 w li lt rgb 'blue' ti 'm',\
'%s' u 1:3 w li lt rgb 'red' ti 'w'", FILENAME, FILENAME);
getchar();
gnuplot_close(h);
// Удаляем временный файл с точками
if (!remove(FILENAME))
printf("Deleting file is complete\n");
else
printf("Temp file does not delete\n");
return 0;
}
Результаты моделирования асинхронного двигателя на языке Си даны на рис. 11.
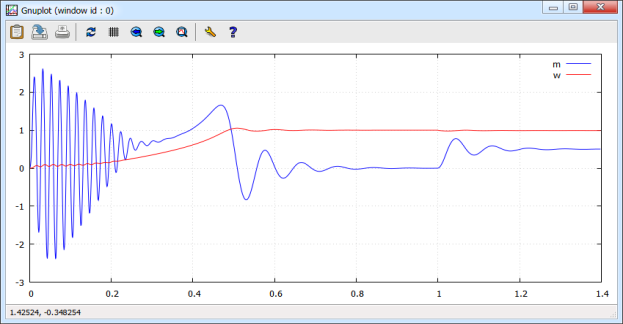
Рис. 11. Графики скорости и электромагнитного момента при моделировании на языке Си
Литература:
- Емельянов А.А., Бесклеткин В.В., Иванин А.Ю., Соснин А.С., Воротилкин Е.А., Забузов Е.И., Волков Е.Н., Вандышев Д.М., Власова А.А., Попов С.Ю. Моделирование асинхронного двигателя с переменными is – ψr на выходе апериодических звеньев в Simulink-Script с базовым вариантом // Молодой ученый. - 2017. - №12. - С. 1-10.
- Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург: УРО РАН, 2000. - 654 с.
- Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.
- Васильев А.Н. Matlab. Самоучитель. Практический подход. – СПб.: Наука и Техника, 2012. – 448 с.
- Васильев А.Н. Программирование на C++ в примерах и задачах. – М.: Издательство «Э», 2017. – 368 с.