Широкий пласт задач теории линейного программирования занимают задачи транспортного типа. Их важность и несомненная значимость в современном мире невероятно велика. Эффективные методы по нахождению оптимального решения Т-задач вручную занимают большое количество времени. Данная работа ориентирована на программный подход для решения транспортной задачи методом потенциалов. Представленная ниже программная реализация позволяет пользователю построить и проанализировать начальный опорный план одним из двух методов: северо-западного угла и минимального элемента, а затем, применив метод потенциалов, найти оптимальное решение и значение целевой функции.
Главное назначение Т-задачи — определить объем перевозок из пунктов отправления в пункты назначения с минимальной суммарной стоимостью перевозок.
Формулировка транспортной задачи представляет собой схему перевозок (рис. 1) и несколько условий, необходимые и достаточные, чтобы найти оптимальное решение. В общем виде она представляет собой следующую схему:
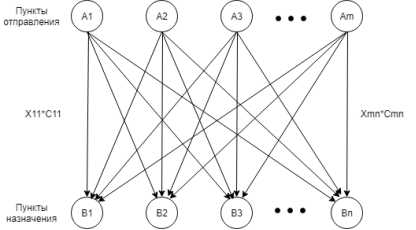
Рис. 1. Графическое представление транспортной задачи
Каждому пункту отправления соответствует количество поставляемого этим пунктом товара — ![]() , аналогично с пунктами назначения —
, аналогично с пунктами назначения — ![]() . Формулами (1) и (2) обозначены основные условия для разрешимости Т-задачи.
. Формулами (1) и (2) обозначены основные условия для разрешимости Т-задачи.
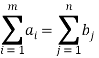 (1)
(1)
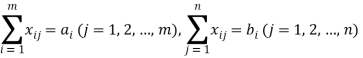 (2)
(2)
Для каждого, полученного в процессе решения, опорного плана вычисляется значение целевой функции ![]() , определяющее минимальную цену на перевозки:
, определяющее минимальную цену на перевозки:
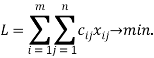
Постановка Т-задачи, применяемая в обозреваемой программе имеет следующий вид: имеется множество пунктов отправления (3)
![]() (3)
(3)
Множество пунктов назначения (4)
![]() (4)
(4)
И матрица тарифов на перевозки между поставщиками и потребителями ![]() , зависящая от предыдущих двух множеств, и содержащая затраты на перевозку
, зависящая от предыдущих двух множеств, и содержащая затраты на перевозку ![]() :
:
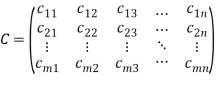
Программная реализация предполагает именно такую форму постановки задачи. Она является понятой для любого пользователя, даже такого, который не знаком с задачами транспортного типа.
Разработка программы проводилась в среде Microsoft Visual Studio 2017 на языке программирования C#. Программа является полностью автономной (состоит из одного файла расширения.exe) и предоставляет пользователю классический, интуитивно понятный оконный интерфейс. Самой значимой частью программы, несомненно, является решение транспортных задач различных размерностей, включающее в себя два основных блока. Первый — это нахождения начального опорного плана методом северо-западного угла или минимального элемента, где пользователь может наглядно увидеть первичную матрицу перевозок. И второй — последующая оптимизация опорного плана методом потенциалов и вывод значения целевой функции.
Давайте найдем оптимальный опорный план для заданной Т-задачи. Предполагается, что пользователь ознакомлен с необходимой теорией. Заполнение полей производится в соответствии с заданными выше условиями.
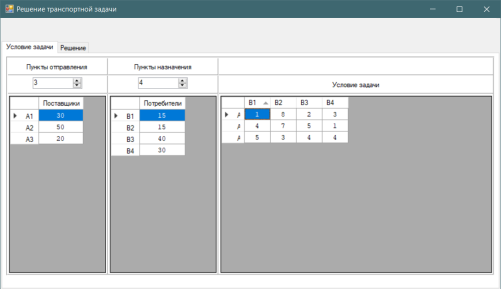
Рис. 2. Заполнение полей условия Т-задачи
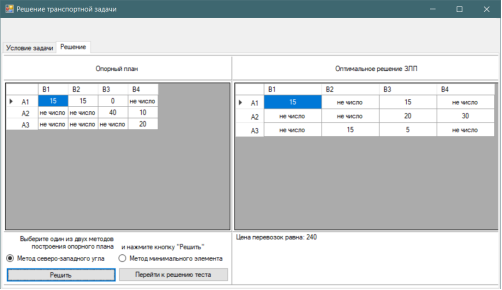
Рис. 3. Решение методом северо-западного угла
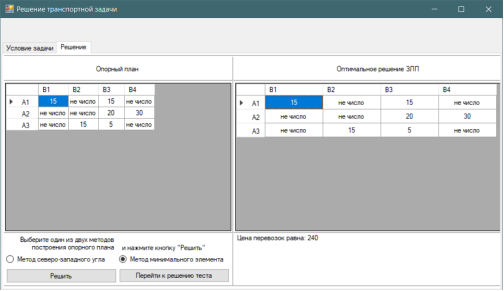
Рис. 4. Решение методом минимального элемента
Помимо решения, программа включает в себя тест, состоящий из 8 вопросов с вариантами ответа на знание теории по методам нахождения предварительного опорного плана и методу потенциалов. Поэтому перед тем, как приступить к непосредственному решению задач, пользователь может проверить свои знания в тесте, решив теоретические и практические задания (рис 5, 6), а затем, скажем, проверить решенную самостоятельно задачу в основной части программы.
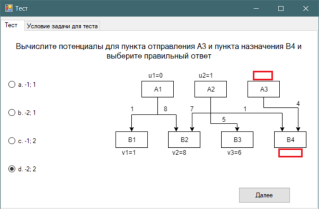
Рис. 5. Один из вопросов теста
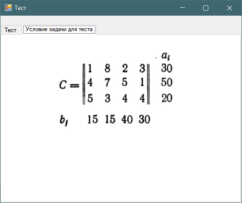
Рис. 6. Условие задачи, которая представлена в тесте
Подводя итог, можно сказать, что в данной статье была представлена работа, имеющая практических интерес среди людей, в частности студентов, кто заинтересован в области задач линейного программирования, изучающей транспортные модели. Была представлена программа, позволяющая пользователю, уже ознакомленному с основными понятиями о транспортных моделях, решать такие задачи разных размерностей, выбирая для построения первичного плана один из двух методов; представленная программная реализация позволяет наглядно продемонстрировать начальный и оптимальный планы перевозок и значение целевой функции конечного опорного плана. Помимо этого, пользователь сможет проверить свои навыки и знания в тесте.
Литература:
- Таха Х. А. Введение в исследование операций — 7-е издание.: Пер. с англ. — Москва: Издательский дом «Вильяме», 2005. — 912 с.
- Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования транспортного типа — М.: Наука, ФИЗМАТЛИТ, 1969. — 384 с.
- Зайченко Ю. П. Исследование операций — Киев: Вища школа. Головное изд-во, 1979 г.
- Кнут Д., Искусство программирования на ЭВМ. 1-й том Основные алгоритмы. Учебное пособие. 3-е изд. — М.: Издательский дом “Вильямс”. — 2000. — 712с.







