Key words: clusters, algorithms, data mining, distance, metrics, normalize, k-means
In [1] [2], the authors have described that clustering algorithms divide a data set into many groups which aims to establish the input dataset in to a set of finite number of groups with respect to some similar quantity. These clustering algorithms can be used both normalized and non-normalized data. If users have normalized data then number of iteration of the algorithms are lesser. So most of the situation normalized data offers good outcome as compared to non-normalizes data. Among of these many clustering algorithms, Density based clustering is the most popular data mining algorithm. This paper, all these clustering algorithms are differentiated according to their own properties. Several issues associated with the use of these clustering techniques are described and emphasizing on some challenges of these algorithms.
Clustering algorithm also uses distance formula. When data is higher dimension [2] then uses Minkowski metric,
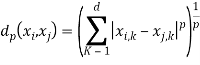 (1)
(1)
where d is dimension of the data.
In case of Euclidean distance, value of p=2, and Manhattan distance the value of p=1.
Some clustering algorithms work at normalized data such as distributed K-Means clustering. Data normalization is the way to linear transforms data to a precise range.
There are several approaches for normalization. The author in [1] have addressed the most popular methods are Min-Max data Normalization, data normalization by Decimal Scaling and Z-score data Normalization. The Min-Max Normalization performed a linear transformation on the original data. In [2], the authors supposed that we have attribute A and Maxa, Mina are the maximum and the minimum values of that attribute. Min-Max normalization maps a value (suppose V of A-V) in the range (0, 1) by computing
![]() (2)
(2)
In Z-score normalization, the values for an attribute (attribute A) is normalized based on the Mean value and Standard Deviation of the attribute(A). Value (suppose V) of attribute A is normalized to v by calculating:
![]() (3)
(3)
where, ![]() is Mean value and σA is standard deviation.
is Mean value and σA is standard deviation.
This method works effectively in two cases: when the actual minimum value and maximum value of attribute (A) is unfamiliar and when there are noise which dictate the min-max data normalization.
In case of Decimal scaling data Normalization the value (suppose V) of attribute (suppose A) is normalized to V’ by calculating:
![]() (4)
(4)
Where j is small integer.
In this article, I analyzed many data mining algorithms which are K-Means clustering, Distributed K-Means algorithm, K-Medoids clustering, Hierarchical clustering, Grid -based clustering and Density based clustering [2] and after analyzing I have shown result according to its performance.
The area of data mining are used various clustering approaches. But every clustering technique has some advantage and disadvantage. Every clustering technique is not appropriate for all the condition. These clustering algorithms work as follows:
K-means clustering technique is a way to organize the data items base on some features into K group. Where K is positive integer. Grouping is completed by reducing the total amount of squares of distances between cluster centroid and data.
K- Medoids Clustering Method is same as K-mean clustering but here calculate medoids instead of mean. Partitioning around medoids works successfully for small data sets it does not works for huge data sets. The time complexity is O (k(n-k)/2) for each repetition where n is number of data objects and k is number of groups.
Difference between K-Means clustering and K-Medoids clustering: K-means Compute group centre but in K-medoids clustering each group’s centroid is denoted by a point with in the groups. K-means is less strong than K-medoids in existence of noise because a medoids are less effected by noisy values. So both clustering algorithms are not gives good performance for noisy data [3]. So new clustering algorithm came for normalized data which called Distributed K-Means clustering.
Hierarchical Clustering technique is a process of cluster (group) analysis which form a hierarchy of clusters (groups). Hierarchical clustering is two type.
1)Agglomerative Hierarchical clustering or AGNES (agglomerative nesting)
2)Divisive Hierarchical clustering or DIANA (divisive analysis).
Grid-based Algorithm makes grid. It works as follows.
1.Label the set of grid-cells
2.Give objects to the appropriate grid cell and calculate the density of every cell.
3.Remove cells, whose density value is below a certain threshold value assume t.
4.Form clusters from adjacent groups of dense cells.
There are two approaches: First is STING (a statistical information Grid approach) and second one is CLIQUE
References:
- Ignatiev N. A. Obobschennye ocenki i lokalnye metriki obyektov v intellektialnom analize dannyh // NUU, Tashkent, 2015.
- Vorontsov K. V. Matematicheskie metody obucheniya po precendentam //Wiki-source MachineLearning.ru
- Ignatyev N. A., Madrakhimov Sh.F., Saidov D. Y. Stability of object classes and selection of the latent features // International journal of engineering technology and sciences (IJETS), 2017, Malaysia, Vol. 7

