В данной работе изложен новый способ геометрического моделирования сечения поверхности туннелей в шахтном строительстве с использованием геометрического преобразования, который позволяет получить новые криволинейные поверхности по заранее заданным условиям.

Ключевые слова: квадратичные геометрические преобразования, туннель, каналовые поверхности, вертикальная ось симметрии, прообраз окружности.

В настоящее время при шахтном строительстве наиболее часто используются каналовые поверхности со сводчатой формой, так как сводчатая форма наиболее эффективна по устойчивости. При этом важно правильное применение крепи и ее несущей способности, и равномерное перераспределение воспринимающей ею нагрузки. При проектировании туннелей часто возникает проблема конструирования поверхности сводчатой формы. На данный момент в основном применяются сплайны или своды, составленные из нескольких дуг кривых 2-го порядка, а это намного усложняет пути решения технологических и конструкторских задач.

Поэтому при проектировании сводов туннелей предлагается применить квадратичные геометрические преобразования, которые позволят смоделировать сложные поверхности туннелей по заранее заданным параметрам и облегчить процесс их проектирования. В связи с этим, разработка новых оптимальных способов и алгоритмов моделирования очень сложных поверхностей туннелей является актуальной проблемой.

Использование геометрических преобразований является одним из способов получения криволинейных поверхностей туннелей в начертательной геометрии. Ранее квадратичные преобразования с вертикальной осью симметрии в начертательной геометрии не использовались. Данная научная статья рассматривает геометрическое конструирование поверхностей туннелей с использованием квадратичного преобразования с вертикальной осью симметрии, которое дает возможность получить новые криволинейные поверхности по заранее заданным параметрам.

Криволинейная поверхность туннелей может иметь поперечное сечение в виде кривой, которая задана на рисунке 1, где h, p — это заданные параметры.

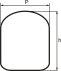
Рис. 1Вид формы сечения туннеля

Сущность предлагаемого способа задания кривой в виде «сечения туннеля» заключается в том, что данная кривая линия может задаваться прообразом-окружностью (рис. 2):

, (1)

и геометрическим преобразованием:

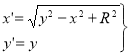, (2)

где x, y — координаты точек прообраза;

x', y'- координаты точек искомой кривой;

r — радиус прообраза-окружности;

t — параметр прообраза;

R — параметр преобразования.

Суть рассматриваемой обратной задачи заключается в том, что по заранее заданным параметрам (h, p) кривой необходимо определить параметры окружности-прообраза и параметр преобразования R.

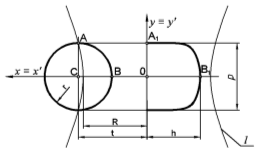
Рис. 2Способ определения значений параметров прообраза и преобразования

Анализ рисунка 2 показывает, что

или (3)

. (4)

На рис. 2 точка В (t- r, 0) преобразуется в точку В₁.

В этом случае расстояние 0В₁ будет равно:

. (5)

x_B, y_B координаты точки В₁ будут иметь следующие значения:

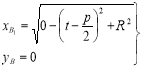. (6)

Далее, из рис. 2 видно, что

. (7)

Из уравнения (7), подставив значение в первое уравнение (6), получим следующее:

. (8)

. (9)

На рис. 2 прообраз n2 и граничная гипербола l пересекаются в точке А (t, ). Далее из точки А опустим перпендикуляр к оси Ох и получим новую точку С (t, 0).

Значения R и t определим в следующем виде:

а) использовав уравнение граничной гиперболы l и координаты точки А (t, ), находим, что:

, (10)

. (11)

б) используя уравнения (9) и (11), находим:

, (12)

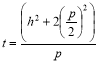. (13)

Тогда, если заранее заданы параметры h, p сечения рассматриваемого туннеля (рис. 2), значения r, t, R можно определить в следующем виде:

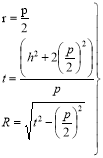. (14)

В этом случае уравнение сечения поверхности или образа определяется следующим способом:

1) сперва находим уравнение прообраза-окружности

. (15)

2) далее находим уравнение преобразования:

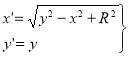. (16)

3) из данной системы уравнений (16) определим:

. (17)

4) далее, подставив уравнение (17) в уравнение (15), находим уравнение сечения поверхности или образа:

, (18)

где t, r, R определяются по формулам (14).

Таким образом, из полученных расчетов можно сделать следующий вывод: использование квадратичного геометрического преобразования с вертикальной осью симметрии позволяет смоделировать новые виды кривых поверхностей туннелей, но при этом каждое сечение поверхности может задаваться одним уравнением.

Литература:

1. Байдабеков А. К. Теория нелинейных преобразований и их применение в науке и технике: автореф. … докт. техн. наук: 05.01.01. — М., 2006. — 36с.
2. Джапаридзе И. С. Геометрические преобразования пространства и их применения в начертательной геометрии. Методы начертательной геометрии и ее приложения. — М.: 1955, — С. 54–222.
3. Нурмаханов Б. Н. Теоретические и прикладные основы проектирования кривых поверхностей и гиперповерхностей методом моноидальных преобразований: автореф.... докт. техн. наук: 05.01.01. — М., 1992. — 36с.
4. Нурмаханов Б. Н., Усупов М. М. Разработка способа задания (1–4)- значных преобразований и их применение в построении кривых — Алматы: Поиск, 1997. — № 1.
5. Нгуен Ван Дьем. К вопросу исследования квадратичного преобразования. // Прикладная геометрия и инженерная графика. — Вып. 3. — Киев, 1956.