Предлагается математическая модель распространения радиосигнала с цифровой модуляцией на основе волнового уравнения в частных производных, решаемого по методу Фурье разделения переменных с комплексным временным базисом, приводится пример моделирования.
Ключевые слова: цифровая модуляция, волновое уравнение, метод Фурье разделения переменных, комплексный временной базис.
Современные системы передачи бинарной информации [1], как правило, используют беспроводные каналы радиосвязи с цифровой модуляцией полезного сигнала: амплитудной или частотной. Значение несущей частоты в таких системах могут достигать нескольких гигагерц, а сами сигналы имеют достаточно сложную форму (пример — системы передачи широкоформатных видеоизображений). По этой причине для описания распространения таких сигналов плохо подходит существующий математический аппарат, а требуется разработка новых математических моделей.
Математическая модель
Разработанная математическая модель построена на основе волнового уравнения в частных производных с двумя слагаемыми со вторыми производными по времени и координате, решаемого по методу Фурье разделения переменных [2]. Однако, вместе с тем, в предложенной модели можно выделить два выгодных отличия от стандартного волнового уравнения и стандартного метода его решения.
Первое отличие состоит в том, что в исходное уравнение дополнительно введено слагаемое с первой производной по координате, за счёт которого учитывается затухание сигнала в пространстве. Второе отличие состоит в возможности задания произвольного возмущающего воздействия в правой части, вследствие перехода к математическому аппарату комплексных чисел (поскольку только он позволяет корректно объединить и чётные, и нечётные гармоники аппроксимируемых функций в методе Фурье).
Для описания распространения радиосигнала произвольной формы было выбрано комплексное уравнение в частных производных второго порядка с постоянными коэффициентами, записанное в виде:
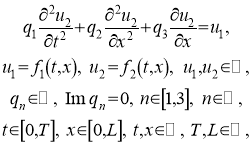 (1)
(1)
c краевыми и начальными условиями:
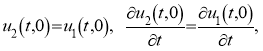 (2)
(2)
![]() (3)
(3)
где: u1(t,x) — комплексная функция входных воздействий (эквивалент напряжения возмущения); u2(t,x) — комплексная искомая функция (эквивалент напряжения распространения); q1,q2,q3 — постоянные комплексные коэффициенты, учитывающие свойства среды; T — период разложения функций по времени; L — период разложения функций по координате; t — время; x –координата.
Решение данного уравнения находится на основе метода Фурье разделения переменных, аналогично действительному случаю, но при использовании временного комплексного базиса разложения функции входных воздействий u1(t,x) и искомой функцию u2(t,x):
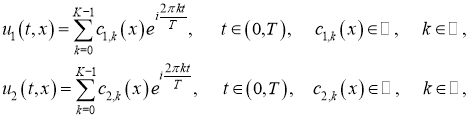 (4)
(4)
где: c1,k(x),c2,k(x) — комплексные коэффициенты разложения функции входных воздействий и искомой функции соответственно; k — индекс коэффициентов разложения (индекс гармоник); K — количество коэффициентов (гармоник) разложения; i — мнимая единица.
После получения на основе последних формул выражений для частных производных и их подстановки в исходное уравнение, согласно алгоритму действий в методе Фурье, для нахождения отдельного коэффициента c2,k(x) приходим к комплексному дифференциальному уравнению вида:
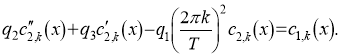 (5)
(5)
При этом коэффициенты разложения входного воздействия c1,k(x) здесь предполагаются уже известными (полученными за счёт предварительного постолбцового разложения функции возмущений u1(t,x) в ходе моделирования). Сам же полезный сигнал с цифровой модуляцией следует размещать в действительной части u1(t,x).
Таким образом, исходное уравнение в частных производных распадается на некоторое множество обыкновенных дифференциальных уравнений, а поиск его общего решения сводится к нахождению всех решений уравнений данного множества, то есть к нахождению всех коэффициентов c2,k(x) с последующим возвратом к начальной формуле разложения искомой функции u2(t,x).
Каждое действительное обыкновенное дифференциальное уравнение для c2,k(x), в свою очередь, решается приближённым методом с использованием разностных отношений вместо производных. Окончательно решение извлекается из действительной части u2(t,x), поскольку для задания возмущения используется действительная часть u1(t,x).
Подчеркнём, что модель работает корректно только для линейного случая, то есть когда в исходное уравнение входят функции от двух аргументов (в данном случае в качестве аргументов выступают время t и координата x). При этом задержка распространения сигнала между двумя точками пространства не учитывается.
Результаты моделирования
В качестве примера приведём результат моделирования радиосигнала с амплитудной цифровой модуляцией (рис. 1). Моделирование осуществлялось в среде MATLAB. Параметру эквивалента напряжения распространения, обозначенного на графике как U, в математической модели соответствует функция u2(t,x).
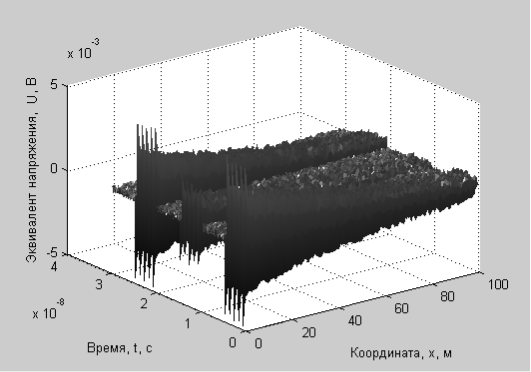
Рис. 1. Пример программной реализация математической модели для сигнала с амплитудной цифровой модуляцией (c учётом шумов передатчика и внешних помех)
Согласно результатам математического моделирования, необходимо отметить следующие важные аспекты относительно предложенной модели. Собственные шумы передающего устройства при небольших значениях уровня их напряжения можно включить в модель как составную часть полного передаваемого сигнала в правой части. Внешние помехи с большими уровнями напряжения следует накладывать после получения u2(t,x) и по принципу суперпозиции.
Заключение
Опираясь на результаты проведённых исследований, в качестве основных преимуществ предложенной математической модели, прежде всего, следует выделить следующие: произвольность задания возмущающего воздействия в правой части уравнения (что даёт возможность задавать сложный сигнал с цифровой модуляцией), учёт затухания сигнала в пространстве (что делает модель приближенной к реальности), а также удобный способ задания свойств конкретной среды или границы раздела нескольких сред (через коэффициенты исходного уравнения).
Вследствие указанных преимуществ, предложенная модель позволяет задавать произвольный полезный сигнал сложной формы, а также учитывать внешние помехи радиоканала и затухание сигнала в пространстве в зависимости от свойств конкретной среды, что открывает возможность моделирования и предварительной оценки качества приёмно-передающих устройств с амплитудной и частотной цифровой модуляцией сигнала.
Последнее крайне важно на этапе проектирования измерительных систем, оперирующих большими объёмами информации (к примеру, широкоформатными видеоизображениями). Примерами таких систем, в свою очередь, могут служить системы видеомониторинга автотранспортных заторов мегаполисов [3–6], а также системы идентификации очагов возгорания лесных массивов по цифровым панорамным аэровидеоизображениям [7,8].
Литература:
-
Feher, K.: Wireless

 Digital
Digital
 Communications: Modulation and Spread Spectrum Applications, Prentice-Hall PTR, 1995
Communications: Modulation and Spread Spectrum Applications, Prentice-Hall PTR, 1995
- Мартинсон Л. К., Малов, Ю. И. Дифференциальные уравнения математической физики: учеб. для вузов. — М.: Изд-во МГТУ им. Баумана, 2002. — 368 с.
- Barhotkin V. A., Minakov E. I., Kalistratov D. S., Kochetkov M. P. (2017) Methods of artificial intelligence in the tasks of information and measuring analysis and digital processing of quasistationary aerovideoimages. Conference Proceedings — 2016 International Conference on Actual Problems of Electron Devices Engineering, APEDE 2016 (Saratov, Russia, September 22–23, 2016), v.2, pp. 305–311, DOI: 10.1109/APEDE.2016.7879017
- Barhotkin V. A., Minakov E. I., Kalistratov D. S., Kochetkov M. P. (2017) Methods of digital filtering in the tasks of information and measuring analysis and compression of panoramic videoimages of road traffic. Conference Proceedings — 2016 International Conference on Actual Problems of Electron Devices Engineering, APEDE 2016 (Saratov, Russia, September 22–23, 2016), v.2, pp. 311–316, DOI: 10.1109/APEDE.2016.7879018
- Калистратов Д. С., Минаков Е. И., Бархоткин В. А., Киселёв А. П. Статистический анализ и компрессия цифровых аэровидеоизображений транспортных потоков: монография / Д. С. Калистратов, Е. И. Минаков, В. А. Бархоткин, А. П. Киселёв, — Тула: Издательство ТулГУ, 2016. — 121 с.
- Минаков Е. И., Калистратов Д. С. Метод геометрической стабилизации квазистационарных аэровидеоизображений в информационно-измерительных системах видеомониторинга / Е. И. Минаков, Д. С. Калистратов // Вестник компьютерных и информационных технологий, — 2016. — № 4 — С.46–49.
- Калистратов Д. С., Минаков Е. И., Мирчук С. Г. Методы идентификации и измерения пространственных координат очагов возгорания лесных массивов по цифровым изображениям: монография / Д. С. Калистратов. Е. И. Минаков, С. Г. Мирчук — Тула: Издательство ТулГУ, 2018. — 116 с.
- Минаков Е. И., Калистратов Д. С., Мирчук С. Г. Модель информационно-измерительной системы видеомониторинга лесных пожаров. / Е. И. Минаков, Д. С. Калистратов, С. Г. Мирчук // Известия Тул ГУ. Технические науки. Вып. 11. Ч. 2. Тула: Изд-во ТулГУ, 2017. С. 194–200.







