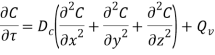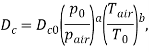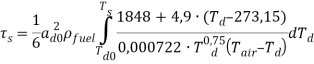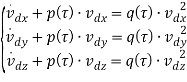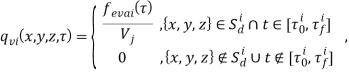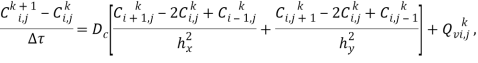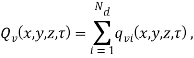Предмет. Процесс смесеобразования, отвечающий за подготовку горючей смеси для последующего сгорания, является важнейшей частью рабочего процесса, как воздушно-реактивных двигателей, так и двигателей внутреннего сгорания. Испарение и диффузия паров жидкого топлива в совокупности являются последней стадией смесеобразования. После распада струи, отдельные капли продолжают движение, испаряясь. Исследование вопроса об испарении движущихся капель представляет из себя достаточно сложную задачу за счет того, что при этом процессе одновременно меняется диаметр капель, их температура, относительная скорость движения, давление насыщенных паров, коэффициент теплопередачи, а также разность температур между поверхностью капли и окружающим воздухом. Таким образом, в данной работе предпринята попытка разработать и реализовать математическую модель процессов испарения и диффузии в условиях, сравнимых с условиями в рабочем объеме камеры сгорания дизелей при впрыске.
Цель. Расчет распределения паров топлива по объему камеры сгорания.
Прочие задачи. Расчет времени существования капли топлива среднего Заутеровского диаметра, расчет траектории движения капли до момента полного испарения, оценка влияния давления и температуры газа на динамику и скорость испарения капель.
Методология. При исследовании использовались известные полуэмпирические зависимости совместно с численными методами решения дифференциальных уравнения в частных производных. Расчеты и визуализация результатов проводились с применением программы математического моделирования MATLAB 2017a.
Ключевые слова: капля топлива, процесс испарения, распределение концентраций.
Математическая модель
В основе математической модели расчета заложена нестационарная диффузия паров топлива, приводящая к установлению равновесного распределению концентраций. В трехмерном пространстве нестационарное распределение концентраций ![]() (
(![]() ) k-го компонента газовой смеси можно описать с помощью уравнения конвекции-диффузии (или уравнение переноса)
) k-го компонента газовой смеси можно описать с помощью уравнения конвекции-диффузии (или уравнение переноса)
|
|
(1) |
где ![]() коэффициент концентрационной диффузии, м2/с;
коэффициент концентрационной диффузии, м2/с; ![]() поле скоростей среды, в которой происходит распределение концентраций, м/с;
поле скоростей среды, в которой происходит распределение концентраций, м/с; ![]() величина, описывающая “источники” или “стоки” концентрации, кг/(м3⋅ с). Далее, индекс k будет опускаться, подразумевая, что речь идет о концентрации паров топлива.
величина, описывающая “источники” или “стоки” концентрации, кг/(м3⋅ с). Далее, индекс k будет опускаться, подразумевая, что речь идет о концентрации паров топлива.
Выражение ![]() описывает явление диффузии. Составляющая
описывает явление диффузии. Составляющая ![]() описывает процесс конвекции, то есть в данном случае перенос концентрации каким-либо потоком совместно со средой. В двигателях внутреннего сгорания примером потока, переносящего концентрации, могут служить поток сжимающегося воздуха при движении поршня или вихрь, создающийся в КС. Для простоты изложения данным элементом уравнения (1) можно пренебречь. Последний компонент уравнения,
описывает процесс конвекции, то есть в данном случае перенос концентрации каким-либо потоком совместно со средой. В двигателях внутреннего сгорания примером потока, переносящего концентрации, могут служить поток сжимающегося воздуха при движении поршня или вихрь, создающийся в КС. Для простоты изложения данным элементом уравнения (1) можно пренебречь. Последний компонент уравнения, ![]() , определяет возникновение или убывание исследуемой величины. В общем случае,
, определяет возникновение или убывание исследуемой величины. В общем случае, ![]() может являться функцией как от концентрации, так и от координат. Примем, что этот элемент будет обозначать источник концентраций паров топлива, испаряющихся с поверхности капель при их неравномерном движении в пространстве.
может являться функцией как от концентрации, так и от координат. Примем, что этот элемент будет обозначать источник концентраций паров топлива, испаряющихся с поверхности капель при их неравномерном движении в пространстве.
В условиях КС поршневых двигателей концентрационный коэффициент диффузии газов и паров топлива
|
|
(2) |
Согласно [2, с. 41] ![]() пропорционален температуре воздуха
пропорционален температуре воздуха ![]() в степени b и обратно пропорционален давление
в степени b и обратно пропорционален давление ![]() в степени a среды, в которой диффундируют газы
в степени a среды, в которой диффундируют газы
|
|
(3) |
где ![]() эмпирические коэффициенты,
эмпирические коэффициенты, ![]() ;
; ![]() коэффициент диффузии при нормальных условиях
коэффициент диффузии при нормальных условиях ![]() , определяемый для дизельного топлива на практике по выражению
, определяемый для дизельного топлива на практике по выражению ![]() [1, с. 70, табл. 2.1].
[1, с. 70, табл. 2.1].
Кроме того, для расчёта необходим коэффициент бародиффузии, то есть коэффициент диффузии, отнесенный к градиенту давления. В предположении о том, что испарение ![]() изотермический процесс [2, с. 42], он может быть найден как
изотермический процесс [2, с. 42], он может быть найден как
|
|
(4) |
где ![]() также коэффициент бародиффузии при нормальных условиях
также коэффициент бародиффузии при нормальных условиях ![]() .
.
Коэффициенты ![]() и
и ![]() связаны соотношением
связаны соотношением
|
|
(5) |
Испарение капли вобъеме КС
В поршневых двигателях тепловой поток может подводиться к капле топлива от нагретых окружающего воздуха, поверхности стенки КС или и от воздуха, и от стенки. В общем случае, преобразование капли жидкого топлива в пар разделяется на два последовательных этапа:
-
Подогрев капли, при котором температура капли возрастает до температуры равновесного испарения
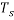 ;
;
- Процесс испарения, который продолжается до полного превращения капли в пар.
Разберем, первый этап, записав закон сохранения энергии для капли топлива, как термодинамической системы
|
|
(6) |
где ![]() изменение внутренней энергии, Дж;
изменение внутренней энергии, Дж; ![]() изменение теплоты, подведенной или отведенной к термодинамической системе, Дж;
изменение теплоты, подведенной или отведенной к термодинамической системе, Дж; ![]() работа, совершаемая над изменением объема рабочего тела, Дж.
работа, совершаемая над изменением объема рабочего тела, Дж.
По определению внутренней энергии
|
|
(7) |
где
Используя закон Ньютона-Рихмана о теплопередаче и пренебрегая радиационным теплообменом, количество теплоты, подведенное к/отведенное от рассматриваемой термодинамической системы, представляется в виде
|
|
(8) |
где ![]() — коэффициент теплоотдачи, определяющий плотность теплового потока при перепаде температур на 1 К, Вт/(м2 ⋅ К);
— коэффициент теплоотдачи, определяющий плотность теплового потока при перепаде температур на 1 К, Вт/(м2 ⋅ К); ![]() — площадь поверхности капли, м3. Для сферической капли диаметром
— площадь поверхности капли, м3. Для сферической капли диаметром ![]() площадь поверхности
площадь поверхности ![]() , а объем
, а объем ![]() [1, с. 279].
[1, с. 279].
Принимая во внимание, что первая стадия изучаемого процесса изохорная, так как при нагреве объем капли не меняется, то ![]() . Тогда выражение (6) с учетом (7) и (8) можно представить, как
. Тогда выражение (6) с учетом (7) и (8) можно представить, как
|
|
(9) |
Начальную массу капли топлива с полностью ![]() можно представить в виде
можно представить в виде
|
|
(10) |
Так как на первом этапе процесса испарения масса капли не меняется, то выражение (9) преобразуется в
|
|
(11) |
Ввиду малых размеров капель ![]() . Следовательно, можно принять число Нуссельта
. Следовательно, можно принять число Нуссельта ![]() [1, с. 82]. По определению числом Нуссельта называется отношением теплового потока за счет конвекции к тепловому потоку за счет тепопроводности.
[1, с. 82]. По определению числом Нуссельта называется отношением теплового потока за счет конвекции к тепловому потоку за счет тепопроводности.
Коэффициент теплопроводности для рабочего тела в зависимости от его температуры с достаточной для практических расчетов точностью найти по формуле, предложенной в [3, с. 131]
|
|
(12) |
Тогда, из определения числа ![]() можно найти зависимость коэффициента теплоотдачи от температуры
можно найти зависимость коэффициента теплоотдачи от температуры
|
|
(13) |
Теплоемкость ![]() для дизельного топлива также может быть выражена как функция от температуры с помощью следующей формулы [1, с. 70, табл. 2.1]
для дизельного топлива также может быть выражена как функция от температуры с помощью следующей формулы [1, с. 70, табл. 2.1]
|
|
(14) |
Объединяя (12), (13) и (14) в (10) и интегрируя по ![]() , получаем время, в течение которого капля топлива прогревается до температуры
, получаем время, в течение которого капля топлива прогревается до температуры ![]()
|
|
(15) |
При приближенном решении интеграла выше получаем
Саму же температура насыщения можно найти как зависимость от ![]() и
и ![]() по соотношению, составленному на основе экспериментальных данных [1, с. 279]
по соотношению, составленному на основе экспериментальных данных [1, с. 279]
|
|
(16) |
причем, ![]() находится в диапазоне температур 623…873 К, а
находится в диапазоне температур 623…873 К, а ![]() берется в бар.
берется в бар.
Когда температура капли достигает значения ![]() начинается вторая стадия ее преобразования в топливные пары
начинается вторая стадия ее преобразования в топливные пары ![]() испарение. На этом этапе рассмотрим закон сохранения массы, имеющий вид
испарение. На этом этапе рассмотрим закон сохранения массы, имеющий вид
|
|
(17) |
Так как суммарный перенос вещества в движущейся среде подчиняется законам, аналогичным законам конвективного теплообмена, то согласно закону Дальтона, массовый расход диффундирующих в воздушном потоке паров топлива определяется следующим соотношением
|
|
(18) |
где ![]() — коэффициент массообмена, с/м;
— коэффициент массообмена, с/м; ![]() — парциальное давление паров топлива над свободной поверхностью, в данном случае поверхностью испарения, Па;
— парциальное давление паров топлива над свободной поверхностью, в данном случае поверхностью испарения, Па; ![]() — парциальное давление на удаленном расстоянии от поверхности испарения в воздушном потоке, Па.
— парциальное давление на удаленном расстоянии от поверхности испарения в воздушном потоке, Па.
Сопоставляя зависимости (9) и (18), можно сделать вывод о подобии процессов тепло- и массообмена. Таким образом, коэффициент ![]() является аналогом коэффициента теплоотдачи
является аналогом коэффициента теплоотдачи ![]() и также зависит не только от свойств жидкой и газообразной фаз топлива, но и от гидродинамических условий (скорость, масштаб и степень турбулентности). Кроме того, на основе подобия данных процессов можно принять равенство числа Нуссельта
и также зависит не только от свойств жидкой и газообразной фаз топлива, но и от гидродинамических условий (скорость, масштаб и степень турбулентности). Кроме того, на основе подобия данных процессов можно принять равенство числа Нуссельта ![]() и числа Шервуда
и числа Шервуда ![]() (диффузионное число Нуссельта).
(диффузионное число Нуссельта).
Тогда, из определения ![]() можно найти коэффициент массообмена
можно найти коэффициент массообмена
|
|
(19) |
где ![]() текущий радиус капли, м. Как упоминалось ранее,
текущий радиус капли, м. Как упоминалось ранее, ![]() .
.
Предполагая сферичность капли топлива, изменение ее массы можно выразить как
|
|
(20) |
Таким образом, из уравнения (17) с учетом, того что текущая площадь поверхности испарения ![]() , а также (18), (19) и (20) получаем
, а также (18), (19) и (20) получаем
|
|
(21) |
Для процесса испарения капли справедливо
|
|
(22) |
где ![]() в бар;
в бар; ![]() эмпирические коэффициенты, для дизельного топлива можно принять
эмпирические коэффициенты, для дизельного топлива можно принять ![]() [4].
[4].
Таким образом, объединяя (21) и (22), получаем дифференциальное уравнение для скорости уменьшения диаметра капли
|
|
(23) |
Обозначим соотношение ![]() константой C, размерность которой составляет м2/с. Интегрируя (23) в интервале от
константой C, размерность которой составляет м2/с. Интегрируя (23) в интервале от ![]() до некого текущего значения
до некого текущего значения ![]() с учетом того, что
с учетом того, что ![]() , получаем время, за которой диаметр капли топлива уменьшился от начального
, получаем время, за которой диаметр капли топлива уменьшился от начального ![]() до текущего
до текущего ![]() в результате испарения
в результате испарения
|
|
(24) |
Полученное выражение описывает закон Срезневского, а константа С, зачастую получаемая опытным путем, называется константой Срезневского.
При полном преобразовании капли в пар ![]() , следовательно, время полного испарения капли топлива
, следовательно, время полного испарения капли топлива
|
|
(25) |
Теперь допустим, что при ![]() масса капли диаметром
масса капли диаметром ![]() составляет
составляет ![]() , тогда ее массу при
, тогда ее массу при ![]() можно найти как
можно найти как ![]() . Выразив из (24) текущий диаметр капли
. Выразив из (24) текущий диаметр капли ![]() , получаем зависимость испарившейся массы топлива с поверхности капли от времени
, получаем зависимость испарившейся массы топлива с поверхности капли от времени
|
|
(26) |
В дальнейшем ![]() каждой капли предполагаются известными, как результат расчета дробления струи.
каждой капли предполагаются известными, как результат расчета дробления струи.
Динамика испаряющейся капли
Запишем второй закон Ньютона, который говорит о том, что в инерциальных системах отсчёта производная импульса материальной точки (испаряющейся капли) по времени равна действующей на неё силе
|
|
(27) |
где ![]() — вектор количества движения капли, (кг ⋅ м)/с;
— вектор количества движения капли, (кг ⋅ м)/с; ![]() — вектор скорости капли соответственно, м/с;
— вектор скорости капли соответственно, м/с; ![]() вектор равнодействующей всех сил, действующих на тело, Н;
вектор равнодействующей всех сил, действующих на тело, Н;
Как было показано ранее масса капли
|
|
(28) |
Тогда левую часть равенства (27) можно представить в виде
|
|
(29) |
Продифференцировав (29), получим
|
|
(30) |
Разберем составляющие вектора ![]()
|
|
(31) |
где ![]() — вектор инерционной силы, возникающий при ускоренном движении системы координат, в которой исследуются перемещение капли, Н;
— вектор инерционной силы, возникающий при ускоренном движении системы координат, в которой исследуются перемещение капли, Н; ![]() — сила гидродинамического сопротивления, Н.
— сила гидродинамического сопротивления, Н.
Для упрощения ![]() учитываться не будет, в предположении об инерционности рассматриваемой системы отчета.
учитываться не будет, в предположении об инерционности рассматриваемой системы отчета.
Допуская движение рассматриваемой материальной точки в неподвижном газе, сила сопротивления может быть выражена как
|
|
(32) |
где ![]() — коэффициент гидродинамического сопротивления, определяющийся зависимостью от числа Рейнольдса [5];
— коэффициент гидродинамического сопротивления, определяющийся зависимостью от числа Рейнольдса [5]; ![]() — площадь миделевого сечения капли, очевидно, зависящая от времени, так как
— площадь миделевого сечения капли, очевидно, зависящая от времени, так как ![]() .
.
Таким образом, из уравнения (27) с учетом (30), (31), (32) можно получить следующее дифференциальное уравнение
|
|
(33) |
где ![]() и
и 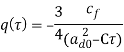 .
.
Спроецировав выражение (33) на оси, например, прямолинейной системы координат, имеем системы дифференциальных уравнений
|
|
(34) |
Начальным условием для данной системы будет являться скорость капли в некоторый начальный момент
Все уравнения системы (37) имеет один и тот же вид — дифференциального уравнения Я. Бернулли. Подобные уравнения можно привести к линейному виду, а, следовательно, найти аналитическое решение. Однако, очевидно, что составляющие системы изменятся при исследовании неинерциальной системы отчета, в которой происходит перемещение капли топлива. Это связано с тем, что проекция силы ![]() на разные оси не всегда будет иметь нулевые значения. В этом случае, для решения системы необходимо использовать такие численные методы, как методы Эйлера или Рунге-Кутта.
на разные оси не всегда будет иметь нулевые значения. В этом случае, для решения системы необходимо использовать такие численные методы, как методы Эйлера или Рунге-Кутта.
Таким образом, с помощью найденных проекций скорости на оси координат можно рассчитать и проекции траектории движения капли в пространстве, причем, начальные координаты капли будут являться начальным условием. Из координат i-ой капли в каждый момент времени составляется множество ![]() . Стоит заметить, что конечная траектории капли также определяется временем ее полного испарения, то есть каждое множество
. Стоит заметить, что конечная траектории капли также определяется временем ее полного испарения, то есть каждое множество ![]() имеет различное количество элементов.
имеет различное количество элементов.
Расчет источников концентраций
Для наглядности расчетов рассмотрим подробнее полет и испарение некой i-ой капли. Ведем некую функцию ![]() , учитывающую долю испаряемых паров топлива с поверхности i-ой капли в каждый момент времени. Кроме этого, данная величина зависит и от пространственных координат ввиду перемещения источника концентраций. Тогда, представим
, учитывающую долю испаряемых паров топлива с поверхности i-ой капли в каждый момент времени. Кроме этого, данная величина зависит и от пространственных координат ввиду перемещения источника концентраций. Тогда, представим ![]() в следующем виде:
в следующем виде:
|
|
(35) |
где ![]() — функция, определяющая массу топлива, испарившегося с поверхности i-ой капли в момент времени
— функция, определяющая массу топлива, испарившегося с поверхности i-ой капли в момент времени ![]() , кг;
, кг; ![]() — величина j-го контрольного объема, в котором в данный момент времени находится капля,
— величина j-го контрольного объема, в котором в данный момент времени находится капля, ![]() ;
; ![]() — множество координат x, y, z, определяемое траекторией движения в пространстве i-ой капли;
— множество координат x, y, z, определяемое траекторией движения в пространстве i-ой капли; ![]() — время начала испарения капли, с;
— время начала испарения капли, с; ![]() — время полного испарения капли, с.
— время полного испарения капли, с.
Для единичной капли функция ![]() определяется как
определяется как
|
|
(36) |
где ![]() — масса испарившегося топлива с поверхности данной капли к моменту времени
— масса испарившегося топлива с поверхности данной капли к моменту времени ![]() , кг (определяется выражением (26));
, кг (определяется выражением (26)); ![]() малое приращение времени, с.
малое приращение времени, с.
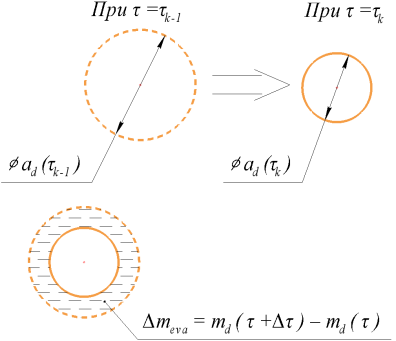
Рис. 1. К определению функции ![]()
Как видно на рис. 2, исследуемое пространство делится не только основной сеткой для решения ДУ, но и вспомогательной, определяющей расположение контрольных объемов
Далее капля перемещается в другой КО (см. рис. 3), а за время перемещения ![]() с поверхности капли испарилась некоторая масса топлива, рассчитываемая согласно (36). Масса этого испарившегося пара складывается с массой, уже содержащемся в объеме
с поверхности капли испарилась некоторая масса топлива, рассчитываемая согласно (36). Масса этого испарившегося пара складывается с массой, уже содержащемся в объеме ![]() . Однако очевидно, что траектория капли проходит через объем
. Однако очевидно, что траектория капли проходит через объем ![]() , и с выбранным
, и с выбранным ![]() расчет испарившейся в нем массы не учитывается. Для решения этой проблемы необходимо уменьшать шаг по времени. Далее, опять же рассматривается следующее положение капли при
расчет испарившейся в нем массы не учитывается. Для решения этой проблемы необходимо уменьшать шаг по времени. Далее, опять же рассматривается следующее положение капли при ![]() .
.
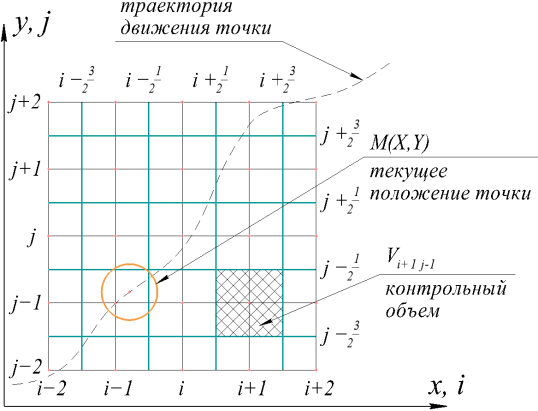
Рис. 2. Положение капли при ![]() на шаблоне разностной схемы
на шаблоне разностной схемы
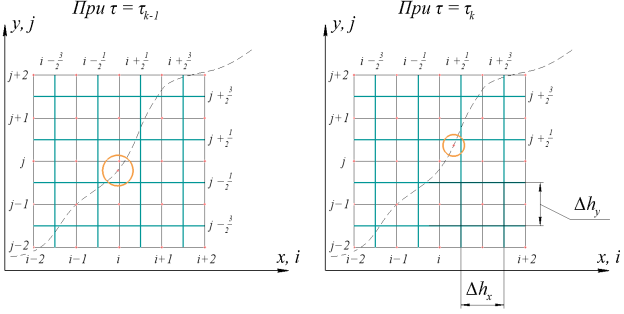
Рис. 3. Положение капли при ![]() (слева) и
(слева) и ![]() (справа) на шаблоне разностной схемы
(справа) на шаблоне разностной схемы
В случае, если капля остается в том же объеме, в котором была и до этого, масса испарившееся за время ![]() суммируется с той, что ранее уже испарилась в данном КО. Так и определяется значение функции
суммируется с той, что ранее уже испарилась в данном КО. Так и определяется значение функции ![]() для одной капли, описанной ранее выражением (35), то есть в точках, не принадлежащих траектории материальной точки, значение
для одной капли, описанной ранее выражением (35), то есть в точках, не принадлежащих траектории материальной точки, значение ![]() .
.
Численный эксперимент
Для простоты изложения рассмотрен случай двумерного пространства, однако, подобные соотношения выводятся и для трехмерного случая. Используя явную разностную схему, уравнение (2) представляется в виде
|
|
(37) |
Индексы ![]() указывают на узлы пространственной сетки, а
указывают на узлы пространственной сетки, а ![]() соответственно временной. Тогда
соответственно временной. Тогда ![]() — шаги данных сеток. Составляющая
— шаги данных сеток. Составляющая ![]() является значением функции
является значением функции ![]() в узле с координатами
в узле с координатами ![]()
Аналогично, можно составить подобную схему и для уравнений из (37), а далее и для нахождения самих траекторий капель. Например,
Для нахождения составляющей ![]() уравнения (2) требуется введение некоторых допущений о протекании процесса испарения. Допустим, что химическая реакция между парами топлива, испарившихся с поверхностей различных капель отсутствует. Тогда, возникшие в каждом конечном объеме концентрации газообразного топлива просто суммируются. Таким образом,
уравнения (2) требуется введение некоторых допущений о протекании процесса испарения. Допустим, что химическая реакция между парами топлива, испарившихся с поверхностей различных капель отсутствует. Тогда, возникшие в каждом конечном объеме концентрации газообразного топлива просто суммируются. Таким образом, ![]() можно рассчитать как:
можно рассчитать как:
|
|
(38) |
где ![]() — число капель, движущихся в рассматриваемом объеме.
— число капель, движущихся в рассматриваемом объеме.
Результаты иобсуждение
Для реализации численных схем, изложенных выше, используется программный комплекс MATLAB 2017b.
На рис. 4 приведена зависимость времени полного испарения капель разных диаметров ![]() при различных параметрах окружающей среды. Данная зависимость дает возможность оценить влияние давления и температуры на протекание процесса испарения: с увеличением температуры или давления капля одного и того же диаметра испаряется медленнее.
при различных параметрах окружающей среды. Данная зависимость дает возможность оценить влияние давления и температуры на протекание процесса испарения: с увеличением температуры или давления капля одного и того же диаметра испаряется медленнее.
Для расчета испарения и динамики нескольких капель задаются такие начальные параметры как, диаметры капель, вектор начальной скорости капли в расчетной сетке. Эти значения предполагаются известными из результатов расчета дробления капель в камере сгорания, поэтому для каждой i-ой капли значения ![]() и
и ![]() задаются случайно с помощью специальной функции из следующих диапазонов: начальный диаметр
задаются случайно с помощью специальной функции из следующих диапазонов: начальный диаметр ![]() мкм, модуль начальной скорости
мкм, модуль начальной скорости ![]() м/с и угол, под которым капля влетает в расчетную область
м/с и угол, под которым капля влетает в расчетную область ![]() . На рис. 5 представлена рассчитанная траектория движения некой единичной капли.
. На рис. 5 представлена рассчитанная траектория движения некой единичной капли.
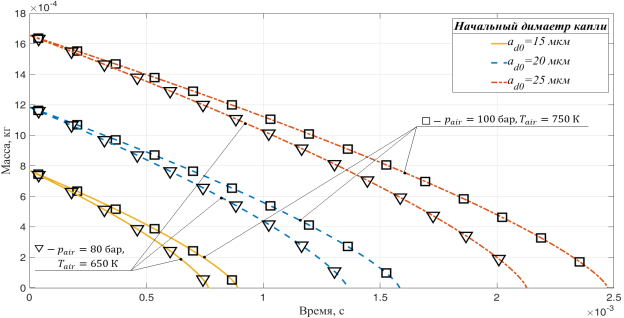
Рис. 4. Изменение масс капель от времени испарения при различных термодинамических условиях
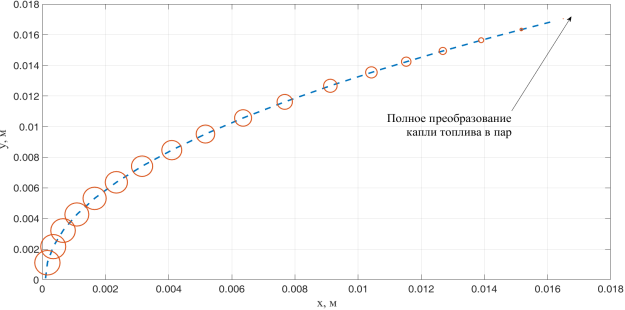
Рис. 5. Траектория движения единичной капли в двумерной постановке (изменение объема капли показано условно)
Итоговым расчетом является решение дифференциального уравнения (2) с помощью разностной схемы (37). На рис. 6 представлено распределение паров топлива по объему камеры сгорания (расчетной области) в разные промежутки времени. По данной зависимости можно увидеть соответствие между распределением паров топлива по расчетной области и траекторией движения капли.
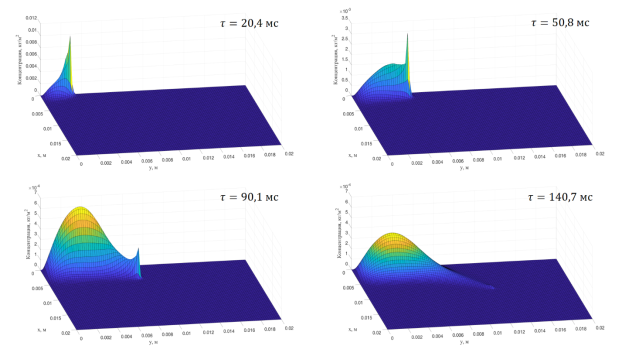
Рис. 6. Расчет распределения паров топлива по расчетной области в двумерной постановке для единичной капли (в горизонтальной плоскости координаты сетки, по вертикали откладывается значение концентрации паров топлива кг/м3)
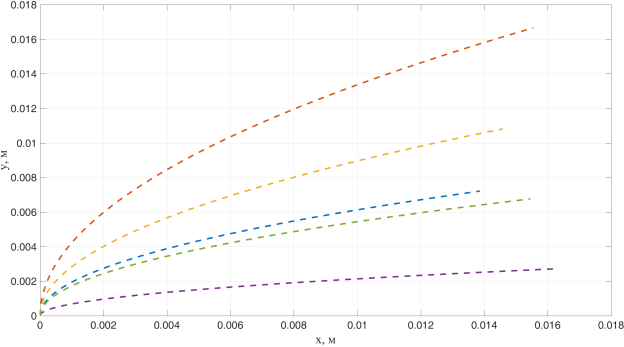
Рис. 7. Траектории движения 5-ти различных капель в двумерной постановке
На рис. 7–8 аналогично представлены траектории 5-ти различных капель и соответственно распределение концентрации паров топлива по расчетной области от испарения данных капель.
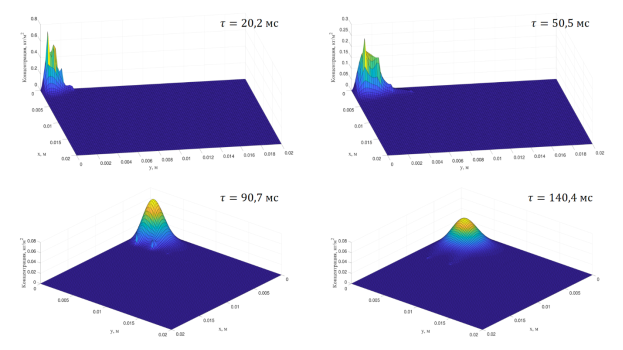
Рис. 8. Расчет распределения паров топлива по расчетной области в двумерной постановке для 5-ти индивидуальных капель
На рис. 9 представлена статистика времени расчета при различных количествах капель, влетающих в расчетную область.
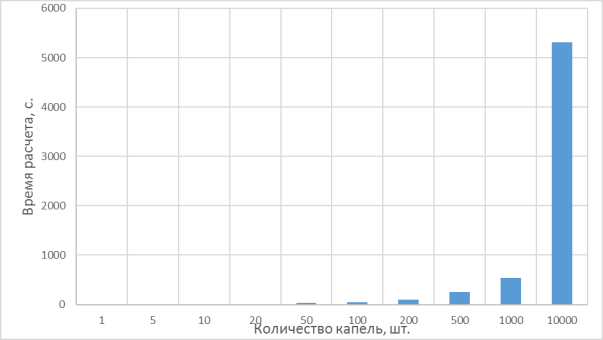
Рис. 9. Зависимость времени счета от количества капель
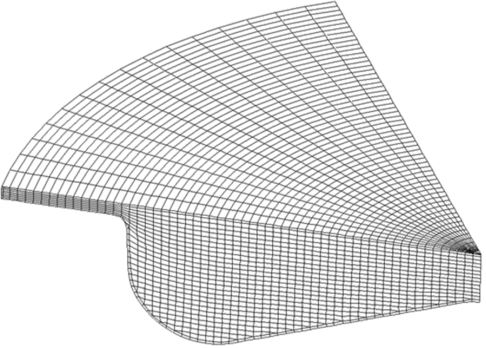
Рис. 10. Трехмерная математическая модель КС дизеля
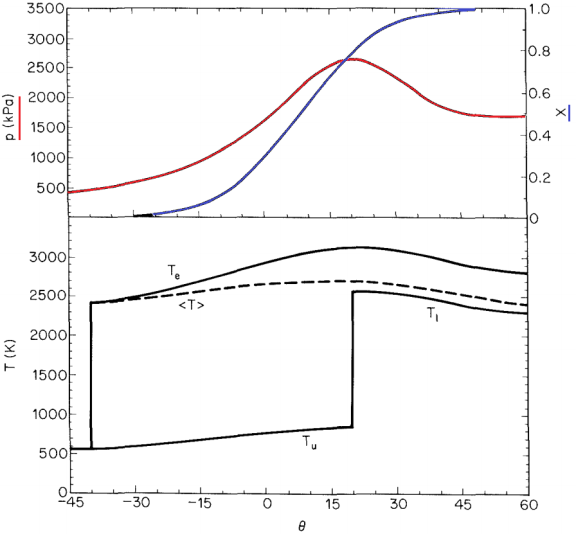
Рис. 11. Изменение параметров состояние газов в КС поршневых двигателей
Таким образом, при исследовании была разработана база для расчета испарения капель в упрощенной постановке, рассчитано время существования капель различного диаметра в неподвижном воздухе, разработана программа для расчета траекторий капель. Созданная упрощенная математическая модель учитывает влияние давления и температуры газа на испарение и динамику капли.
В дальнейших исследованиях необходимо уточнить эмпирические зависимости (концентрационный коэффициент диффузии газов и паров топлива ![]() , давление насыщенных паров
, давление насыщенных паров ![]() ), верифицировать созданную модель с уже существующими, учесть сложность геометрии расчетной области (см. рис. 10), усовершенствовать газодинамическую модель (влияние давления и температуры на траекторию капель), учесть изменение параметров состояния газов в течение всего процесса испарения (см. рис. 11), спланировать эксперимент.
), верифицировать созданную модель с уже существующими, учесть сложность геометрии расчетной области (см. рис. 10), усовершенствовать газодинамическую модель (влияние давления и температуры на траекторию капель), учесть изменение параметров состояния газов в течение всего процесса испарения (см. рис. 11), спланировать эксперимент.
Литература:
- Теория поршневых двигателей. Специальные главы: учебник для вузов / Кавтарадзе Р. З. — 2-е изд., испр. и доп. — Москва: Издательство МГТУ им. Н. Э. Баумана, 2016. — 589, [3] с.: ил.
- Справочник по теплофизическим свойствам углеводородных топлив и их продуктов сгорания / Дубовкин Н. Ф. — Мосэнергоиздат, 1962. — 288 с.: ил.
- Локальный теплообмен в поршневых двигателях: учебник для вузов / Кавтарадзе Р. З. — Москва: Издательство МГТУ им. Н. Э. Баумана, 2016. — 515, [5] с.: ил.
- Процессы в перспективных дизелях / Под ред. А. Ф. Шеховпова. Харьков: Изд-во «Основа» при Харьковском государственном университете, 1992.
- Drag Coefficient / [Электронный ресурс]; URL: http://www.thermopedia.com/content/707/