ПИ-реттегіш пен қозғалтқышты модельдеу Matlab Simulink компонентінің S-Function көмегімен іске асырылды, ол бағдарламалық код түрінде модельді іске асыруға мүмкіндік береді.
1-суретте нейрожелілік реттегіші бар жүйенің моделі ұсынылған.
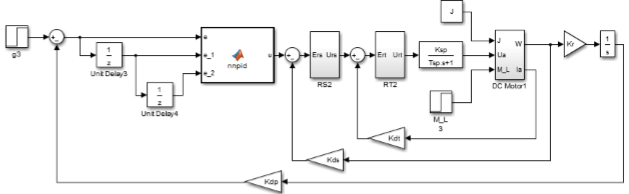
Сурет 1. Нейрожелілік реттегіші бар қадағалау жүйесінің Simulink-моделі
1-суретте келтірілген пайдаланушының nnpid блогы НР алгоритмін іске асырады. Оның кірісіне қате e келіп түседі, қате кідірісі бір таймерлік цикл және екі цикл. Блок шығысы орналасу контурына басқарушы әсер болып табылады [1].
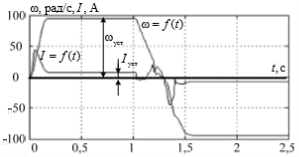
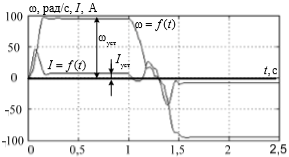
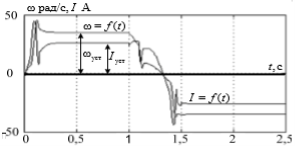
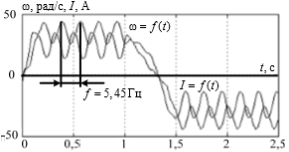
Төменде жүйе жұмысының нәтижелері келтірілген. 2-суретте жүйенің сатылы әсерге реакциясы көрсетілген. Бұл кезде кезектегі сатыны берген кезде жүйеде инерция моменті өзгереді. Бастапқыда ол J= 0.0835 кг*м2 тең, ол 3 есе ұлғаяды 3J=0.2505 кг*м2 және соңғы тапсырма алдында бастапқы шамаға J/3=0.0278 кг*м2 қатысты 3 есе азаяды. 3-суретте синусоидалды тапсырманың жүйе кірісіне келіп түсетін шығыстық шаманың графигі келтірілген. Моменттің өзгеру жағдайлары өзгеріссіз қалады. Өзгеру уақыты 0,5 және 1 секунд.
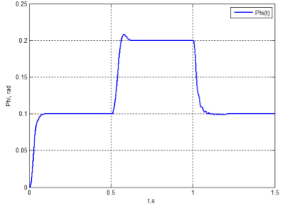
Сурет 2. Инерцияның өзгеру моменті кезінде сатылы әсерге нейрожелілік реттігіші бар жүйенің реакциясы
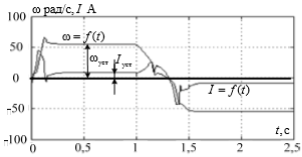
Жүйенің екі түрлі нейрожелілік басқару кезінде жұмыс нәтижелерін салыстыра отырып келесі қорытынды жасауға болады: ПИД-реттегіші бар дәстүрлік басқару әдісімен салыстырғанда екі әдіс те реттеу сапасын едәуір жақсартады.
Гибридті нейро-ПИД басқару жағдайында жүйенің адаптациясы тез арада жүзеге асырылады, алайда нейрореттегішпен салыстырғанда сапасы төмен болады. Бұл туралы қайта реттеу шамасы бойынша айтуға болады.
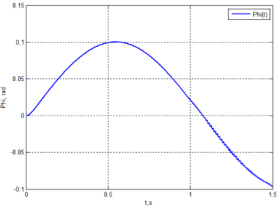
Сурет 3. Инерцияның өзгеру моменті кезінде синусоидалды әсерге нейрожелілік реттегіші бар жүйенің реакциясы
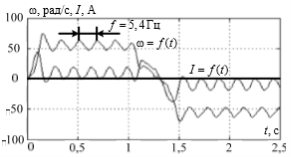
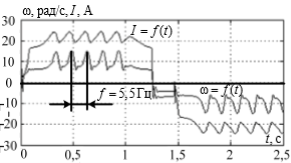
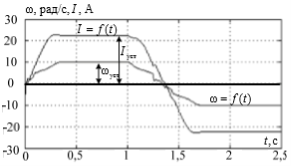
4-суретте модельдеу нәтижелері келтірілген: сол жағында – нейрожелілік реттегіштің көмегімен алынған өтпелі процестер, ал оң жақта – реттегіштің көмегінсіз алынған өтпелі процестер [1]. Графиктерден көрінетіндей автоауытқуларды пайда болу диапазонында жоюға мүмкін болды және жетек статикалық қатесіз берілген жылдамдықта жұмыс істейді.
|
Нейрожелілік реттегіш пен ПИ-реттегіш көмегімен алынған өтпелі процестер |
ПИ-реттегіштің көмегімен алынған өтпелі процестер |
|
|
|
|
а | |
|
|
|
|
б | |
|
|
|
|
в | |
|
|
|
|
г | |
Сурет 4. Нейрожелілік реттегіші бар және жоқ кезіндегі тоқ пен жылдамдықтың өтпелі процестері: а – 95 рад/с; б – 55 рад/с; в – 35 рад/с; г – 10 рад/с
Соңғы кездері, тез көбейіп жатқан жасанды нейрондық желілерді қолдануына байланысты, дамыған нейронды есептеулерді, қосымша бағдарламалық құрал мен аппараттық өнімдерін өндіру үшін қажетті есептеулерді жиі іске асуда.
Ол нейрожелілер мен нейронды есептеулерді іске асыруда бағдарламалық шешім болып табылатынын атап өткен жөн. НЖ модельдеу үшін ең көп таралған бағдарламалық пакетін Mathworks фирмасының Matlab деңгейіндегі Neural Network Toolbox өнімі болып табылады [2]. 5-суретте НЖ және Neural Network Toolbox оқыту процесі көрсетілген.
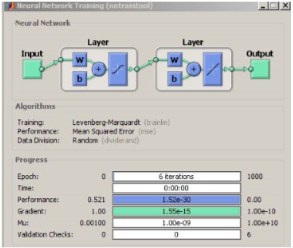
Сурет 5. НЖ және Neural Network Toolbox оқыту процесі
Бұл пакет, НЖ құру мен оқытудың мысалдары ретінде үлкен базаға ие, топологиялық мәліметтерді алуда және оқу-әдістемелік тәжірибесі жоқ пайдаланушылар үшін қолайлы болып есептелінеді.
Нейрондық желілердің Neural Network Toolbox арқылы жиналған деректерін (болжау, бөлуіне) талдау және кез келген жабдықты өлшеу немесе басқа бағдарламаларды нақты уақыт режимінде алынған ақпаратты өңдеу үшін пайдалануға болады. Сондай-ақ, деректер жағдайында қажетті өңдеу қуатын қамтамасыз ету үшін көп ядролы процессорлар немесе Matlab бағдарламасының компьютерлік кластерлерін есептеу және бөлуге болады.
Әдебиет:
- Круглов В.В., Дли М.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети. – М.: ФИЗМАТЛИТ, 2001. – 201 с.
- Медведев В.С., Потемкин В.Г. Нейронные сети. MATLAB6. Кн. 4. Пакеты прикладных программ / Под общ. ред. В.Г. Потемкина. – М.: ДИАЛОГ-МИФИ, 2002. – 496 с.