В статье приводятся исследования по индексу геомагнитной активности часового разрешения, что характеризует степень возмущения магнитосферы Земли. Приводится статистический поход по прогностическому моделированию индекса Dst часового разрешения без процедур экстраполяции.
Ключевые слова: гравитационные силы, геомагнитный индекс, прогностическая модель, регрессия, адекватность.
The article presents studies on the geomagnetic activity of hourly resolution, which characterizes the degree of perturbation of the Earth’s magnetosphere. A statistical approach to the predictive modeling of the Dst index of hourly resolution without extrapolation procedures is given.
Keywords: gravitational forces, geomagnetic index, prognostic model, regression, adequacy.
Исследования индексов геомагнитной активности (ГМА) [1] обусловлены необходимостью прогнозирования электромагнитного состояния околоземной среды. Это позволяет минимизировать негативное воздействия солнечного ветра на работу спутниковых и наземных радиотехнических систем, электрических линий передач, электростанций, железнодорожной автоматики.
В связи с этим, представляется актуальным исследование индекса ГМА — Dst часового разрешения, численные значения которых характеризуют степень возмущения магнитосферы Земли.
Индексы ГМА, как правило, испытывают циклические и случайные колебания, которые ведут к непостоянству их средних величин за большие интервалы времени. Поэтому методы прогнозирования являются чисто эмпирико-статистическими, опирающимися исключительно на всевозможные статистические связи между различными характеристиками ГМА.
В последнее время увеличивается количество работ по исследованию влияния сил гравитации на природные процессы [2,3].
Изложим концепцию методики прогнозирования индекса Dst на основе перераспределения гравитационных сил в солнечной системе относительно конкретной географической точки Земли.
Постановка задачи. Согласно вышеизложенному, индекс Dst зависит от степени возмущения магнитосферы Земли солнечным ветром. Качественное и количественное значение индекса Dst зависит от многих факторов, которые условно можно разбить на следующие категории:
- Категория «Место наблюдения (M(i))».
- Категория «Время». Индекс Dst меняется в течение суток t.
- Категория «Дата (Время года)». Индекс Dst меняются в течение года.
-
Категория «Гравитационные силы». Индекс Dst зависит от распределения масс в солнечной системе относительно точки наблюдения
 .
.
Таким образом, для получения эффективных прогнозов по динамике индекса Dst, необходимо производить построение регрессионного уравнения в виде:
![]()
В этом случае, математическая модель прогноза индекса Dst будет зависеть от многих факторов, которые в свою очередь непрерывно меняются во времени и пространстве. Это приводит к нарушениям требований метода наименьших квадратов (МНК) [4]. Для повышения однородности исходной выборки данных при решении задачи прогнозирования индекса Dst предлагаются следующие процедуры.
Фактор «Место наблюдения». Любая географическая точка характеризуется следующими характеристиками: географическая широта и долгота, высота над уровнем моря, степень загрязненности атмосферы. Используя эту процедуру, мы повышаем однородность исходного массива данных за счет исключения из рассмотрения характеристик, описывающих специфические особенности места наблюдения.
![]()
Фактор «Время суток» и «ДАТА (Время года)».
Можно констатировать, что использование процедуры 2 позволяет параметры категорий «Время», «Дата» перевести в разряд констант и, соответственно, задача сводится к определению динамики индекса Dst на основе гравитационных сил солнечной системы.
![]()
Предлагаемая процедура позволяет повысить однородность исходной выборки данных, но при этом построение прогностической модели индекса Dst для каждого момента времени и дня года в отдельности.
Фактор «Гравитационные силы». На предыдущих этапах при помощи процедур влияние параметров факторов «место наблюдения», «время суток» и «время года» были сведены к постоянному уровню, что позволило исходную задачу (1) преобразовать к виду (3).
Построение моделей прогноза производилось в виде регрессионных уравнений. При этом использовались только те характеристики приливообразующего потенциала, которые имеют достоверную корреляционную связь со значениями индекса Dst (p<0,05).
В нашем случае из кинематических характеристик в рассмотрение были включено только смещение (14850 характеристик). Чтобы исключить нарушение предположений о ранге МНК гравитационные волны были объединены в 6 групп в зависимости от проекции (mer, par, wer) и характера корреляционной связи с Индексом Dst (r>0, r<0): S1 (mer, r +), S2 (mer, r -), S3 (par, r +), S4 (par, r -), S5 (ver, r +), S6 (ver, r -).
Прогнозирующие правила индекса Dst строились в виде простой регрессии от каждой из этих сумм. За окончательный результат принималась среднеарифметическая значений простых регрессий.
Изложенная методика была апробирована при прогнозировании индекса Dst часового разрешения. Исходный массив был взят из интернет-источника Мирового Центра Данных по солнечно-земной физике (http://www.wdcb.ru/stp/index.ru.html) за период 1938–1987 годы. Общее количество замеров составило 17824, получено 384 прогностические модели индекса Dst.
О степени соответствия прогностических моделей исходным статистическим данным Dst. можно судить по рис.1.
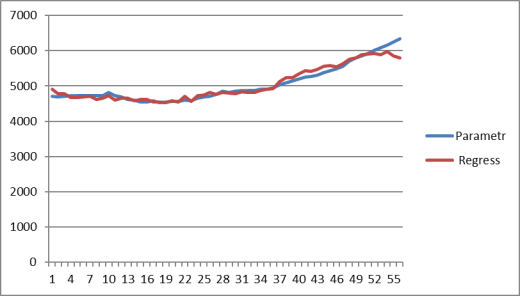
Рис.1. Графики значений индекса Dst. и его отклонение от реальных значений
Преимуществами предлагаемого подхода прогнозирования является отсутствие процедур экстраполяции, т. е. точность прогноза индексов Dst не зависит от срока прогнозирования.
Литература:
- Огурцов М. Г.: 2005. Современные достижения солнечной палеоастрофизики и проблемы долговременного прогноза активности Солнца. Астрономический Журнал. Т. 82, № 6,
- Амиантов А. С., Зайцев А. Н., Одинцов В. И., Петров В. Г. Вариации магнитного поля Земли. М., 2001.
- Константиновская Л. В. Положение планет и долгосрочное прогнозирование. — Математические методы анализа цикличности в геологии, вып.6, РАЕН, М., 1994, с.113–117.
- Дубров А. М., Мхитарян В. С., Трошин Л. И. Многомерные статистические методы. М.: Финансы и статистика, 2000. — 352 с.

