Наряду с исследованием и изучением тепловых процессов, сегодня, благодаря стремительному прогрессу в области нанотехнологий, активно происходит изучение физических свойств и характеристик коллоидных суспензий, находящихся как в статическом состоянии, так и при различных нагрузках, включая тепловые. Данная тематика актуальна, и любые продвижения в исследованиях характерны не только новыми теоретическими познаниями, но и зачастую несут в себе значения прикладного характера.
Коллоидные суспензии или, как сейчас их принято называть, наножидкости, широко применяются в различных сферах нанотехнологии. Например, их используют в химических процессах (катализе), при создании новых лекарств, смазочных материалов и т.д.
Наножидкости участвуют в создании эффективных охлаждающих систем и управления большими тепловыми потоками. Они характеризуются особыми свойствами переноса. Существуют феноменологические подходы при описании процессов переноса в таких отрытых системах как наночастицы + жидкость + лазерное излучение, основанные на первых принципах: законах сохранения энергии и массы. Решение подобной системы балансных уравнений, содержащих конкретные теплофизические и оптические параметры, даёт возможность исследовать динамику концентрации наночастиц, определить температурные поля и изучить нелинейные оптические свойства наножидкости. Однако, упомянутая система уравнений слабо исследовалась аналитически и численно, кроме того недостаточно изучены эффекты самовоздействия световых полей в наножидкости на фоне зависимости коэффициента поглощения излучения от концентрации частиц, а также вклад термодиффузионных и электрострикционных механизмов оптической нелинейности, практически не рассматривались вопросы формирования диссипативных структур и процессы распространения концентрационных волн переключения применительно к упомянутым выше открытым системам.
Анализируя все вышесказанное на данном этапе, можно сформулировать цель научного исследования, по результатам которого и была написана данная работа: теоретическое исследования динамики поведения наночастиц в наножидкости, используя методы математического моделирования процессов тепломассопереноса.
В качестве объекта исследования выступила: жидкофазная среда с наночастицами, находящаяся под воздействием лазерного излучения, конкретнее, в качестве наножидкости выступила дистиллированная вода с частицами латекса.
Система уравнений, основанная на законах сохранения энергии и массы, описывающая эти процессы, была представлена в работах авторов, однако, для полного понимания картины происходящих физических процессов, описывающих эволюцию наночастиц в жидкости, находящейся под воздействием светового поля без учёта конвекции, было получено дифференциальное уравнение в частных производных (1) с начально краевыми условиями (2) и (3):
![]() (1)
(1)
![]()
![]()
![]() (2)
(2)
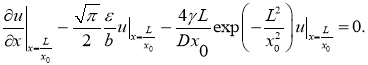 (3)
(3)
Заметим, что уравнение (1) записано таким образом, чтобы в дальнейшем можно было выделить вклады в динамику концентрации от термодиффузии и электрострикции (второе и третье слагаемые соответственно в правой части уравнения).
Численные оценки коэффициентов в краевом условии (3) показывают, что двумя последними слагаемыми можно пренебречь. В этом случае краевые условия становятся однородными:
![]()
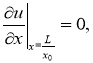 (4)
(4)
Суммируя все вышесказанное, можно записать математическую постановку для описания эволюция наночастиц в жидкости, находящейся под воздействием светового поля без учёта конвекции:
![]() (5)
(5)
с начальными и краевыми условиями
![]()
![]()
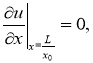 (6)
(6)
![]()
На следующем этапе, математическая модель (5) – (6) при помощи метода конечных разностей была сведена к системе линейных алгебраических уравнений для решения которой был реализован численный метод, при помощи средств высокоуровневого языка программирования C++. Позже на основе рассчитанных данных были построены различные графики при помощи пакета прикладных программ для решения задач технических вычислений Matlab.
Исходя из математической постановки (5) – (6) было принято решение проводить численный эксперимент при фиксированном параметре ![]() характеризующем зависимость коэффициента теплопроводности от концентрации, однако варьировать показателем
характеризующем зависимость коэффициента теплопроводности от концентрации, однако варьировать показателем ![]() , отвечающим за вклад в конценрационный поток от электрострикции, для исследования его вклада в процесс протекания физических процессов тепломассопереноса.
, отвечающим за вклад в конценрационный поток от электрострикции, для исследования его вклада в процесс протекания физических процессов тепломассопереноса.
Например, на рисунке 1 изображены зависимости решения от времени при фиксированных пространственных координатах, при ![]() - сплошная линия, и при
- сплошная линия, и при ![]() - пунктирная линия при
- пунктирная линия при ![]() . Для наглядности и более детального исследования, приведены графики зависимости решения от времени при фиксированных пространственных координатах при
. Для наглядности и более детального исследования, приведены графики зависимости решения от времени при фиксированных пространственных координатах при ![]() и при
и при ![]() .
.
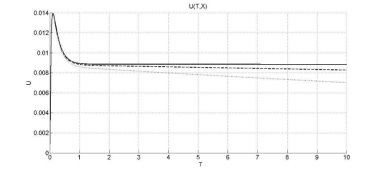
Рисунок 1 – Полученные зависимости решения от времени при следующих значениях параметров ![]() Сплошной линии соответствует
Сплошной линии соответствует ![]() , пунктирной -
, пунктирной - ![]() , а прерывистой –
, а прерывистой – ![]() .
.
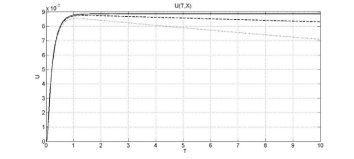
Рисунок 2 – Полученные зависимости решения от времени при следующих значениях параметров ![]() Сплошной линии соответствует
Сплошной линии соответствует ![]() , пунктирной -
, пунктирной - ![]() , а прерывистой –
, а прерывистой – ![]() .
.
Графики, изображенные на рисунках 1 – 2, позволяют сделать следующие выводы:
- Учёт параметра m приводит к уменьшению со временем величины концентрации частиц в различных точках пространства.
- Скорость этого убывания существенно зависит от знака этого параметра и расстояния от начала координат.
На следующем этапе были построены графики зависимости решений от пространственных координат при фиксированной переменной времени. Для выявления визуальных отличий и более детального изучения, было принято решение построить графики, прибегая к более мелкому масштабированию (рисунок 3).
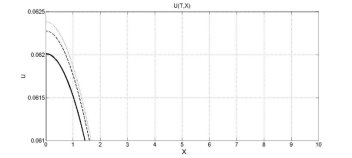
Рисунок 3 - Зависимости решений от координат (t=0.02), полученные при m= 0 – пунктирная линия, m= 0,1 – прерывистая линия и m=-0.1 – сплошная линия, ![]()
Далее, для более детального представления физических процессов, на основе полученных численных результатов, была построена поверхность, изображенная на рисунке 4.
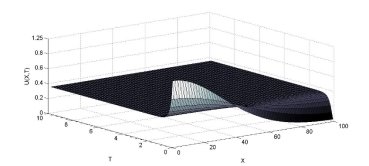
Рисунок 4 – Графическая зависимость решения от пространственной переменной и переменной времени при ![]()
На основе всего вышеописанного можно сделать следующие выводы:
- Если при изучении процессов тепломассопереноса, происходящих в наножидкости, находящейся под воздействием лазерного облучения с гауссовым профилем интенсивности пренебречь конвекцией, то в рамках линейного приближения по концентрации с течением времени наблюдается «расплывание» изначальной кривой распределения интенсивности. Заметим, что этот результат качественно отличается от выводов, полученных в работе. Мы полагаем, что этот факт связан с использованием в этой работе приближения очень малых возмущений концентрации, наш подход свободен от этого ограничения.
- Благодаря численному эксперименту была выявлена значимая роль электрострикционного эффекта в переходном режиме динамики наночастиц. Работоспособность и точность предложенного метода проводилась на ряде численных экспериментов.
- Разработанные методы и представленные результаты работы могут быть полезны специалистам в сфере теплоснабжения, а также другим исследователям подобной тематики.
Литература:
- Рудяк В. Я., Белкин А. А., Томилина Е. А., О коэффициенте теплопроводности наножидкостей, Письма в ЖТФ, 36:14 (2010), 49
- Виноградова П.В., Ливашвили А.И., Манжула И.С., Моделирование процессов тепломассопереноса в наножидкости // Хабаровск: Тихоокеанский государственный университет, 2017, с. 23 – 27.
- Виноградова П.В., Ливашвили А.И., Манжула И.С., Численное моделирование процесса термодиффузии в наножидкости // Хабаровск: Дальневосточный государственный университет путей сообщения, 2017, с. 275 – 279.

