О методе подготовительных задач



Потребность в подготовительных задачах при изучении доказательств особенно ощутима в тех случаях, когда в доказательстве используются новые непривычные для учащихся рассуждения, которыми «с ходу» овладеть достаточно трудно. Подготовительные задачи позволяют сформировать у учащихся некоторый опыт в проведении таких рассуждений и тем самым облегчить усвоение доказательства. [1. c 12]

Сказанное, например, относится к доказательству теоремы о площади криволинейной трапеции. Эта теорема является «центральной» в теме «Интеграл». С её помощью геометрический смысл понятия первообразной, а позднее обосновывается формула Ньютона-Лейбница. В действующих учебниках она формулируется следующим образом. Теорема. Пусть f-непрерывная и неотрицательная на отрезке [a;b] функция, S-площадь соответствующей криволинейной трапеции (рис 1). Если F есть первообразная для f на отрезке [a;b], то S= F(b)-F(a).

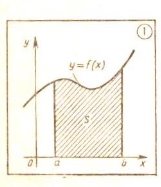
Выясним, какие подготовительные задачи целесообразно рассмотреть при изучении данной теоремы.

1. Необходимо, прежде всего учесть что в доказательстве известные учащимся понятия (приращение аргумента, приращение функции) используются в специфических условиях: функция S(x) задается не формулой, таблицей, графиком, а указанием геометрической фигуры — криволинейной трапеции; аналогичным образом представляются её значения S(x), S(x+ Δx) и приращение ΔS =S(x+ Δx) — S(x).Такая интерпретация значений функции и её приращения является новой для учащихся. Поэтому доказательство, полезно предварить следующим заданием: На рисунке 2 площадь криволинейной трапеции S есть функция от х. Укажите на этом рисунке фигуры площади которых равны S(x), S(x+ Δx) и ΔS =S(x+ Δx) — S(x).

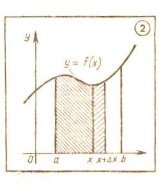
2. Определение производной тоже применяется в новой ситуации — к функции S(x). Учащихся можно подготовить к этому поставив такое задание: «Запишите определение производной применительно к функции S(x)».

3. В теореме на наглядном уровне используется понятие непрерывности функции. С этим понятием следует предварительно поработать: «Пусть f(x) — функция непрерывная в точке х₀. Отметьте на оси абсцисс точки х₀, x₀+ Δx и точку С, лежащую между ними (рис 3). Пусть Δx стремится к 0. К чему стремится f(с)?»

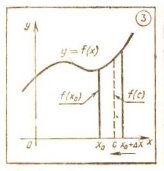
4. В теме «Интеграл» важную роль играет утверждение о том, что площадь криволинейной трапеции с основанием Δx и высотой f(с), где с — некоторая точка отрезка [х; x+ Δx]. Существование такой точки с как раз и утверждает данный факт.

Учащихся полезно отдельно ознакомить с данным фактом, проиллюстрировав его на рис. 4 и предложив следующее задание: «Дана криволинейная трапеция с основанием Δx. Постройте прямоугольник, у которого основание Δx, а площадь равна площади криволинейной трапеции».

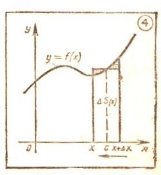
5. При доказательстве теоремы о площади криволинейной трапеции определение первообразной применяется в новых обозначениях. Перед рассмотрением доказательств учащимся полезно поупражняться в оперировании с новыми обозначениями: «Пусть S(x) — первообразная f(x). Поясните, что это означает. Пусть S(x) — одна из первообразных для функции f(x). Запишите формулу для общего вида первообразных функции f(x)».

После разбора указанных подготовительных заданий можно перейти к изложению доказательства теоремы, которое целесообразно разбить на три части.

а) Введение функции S(x).

Рассмотрим функцию S(x), определенную на отрезке [a;b] которая выражает зависимость площади криволинейной трапеции от аргумента х. Дадим аргументу х приращение Δx такое, что а≤ x+ Δx≤ b. Тогда приращение функции S(x) в точке х равно ΔS(x) =S(x+ Δx) — S(x) (Δx полагаем положительным).

б) Доказательство того, что S'(x)= f(x) для всех х принадлежащих [a;b]. Согласно определению производной имеем: S'(x) равна пределу отношения ΔS(x) к Δx, при стремлении Δx к нулю. Площадь ΔS(x) криволинейной трапеции с основанием Δx можно заменить равной площадью прямоугольника с основанием Δx и высотой f(с), где с принадлежит [х; x+ Δx]: ΔS(x) = f(с) Δx Тогда S'(x) равна пределу f(с) при Δx стремящемуся к нулю. Поскольку с лежит между х и x+ Δx, то при Δx стремящемуся к нулю точка с стремится к х, а f(с) стремится к f(х). Поэтому предел f(с) равен f(х), при Δx стремящемся к нулю. Итак, S'(x)= f(x).

в) Доказательство равенства S = F(b) –F(a).

Мы доказали, что S(х) — первообразная для f(x) на этом же отрезке. Следовательно функции S(x) и F(х) отличаются друг от друга на некоторую константу С: S(x) = F(х) +С. При х=а это равенство примет вид 0= F(a)+С. Отсюда С = — F(a). При х = b равенство S(x) = F(х) + С примет вид S(b) = F(b) + С. Поэтому S=S(b)= F(b)-F(a), что и требовалось доказать.

Отметим, что использование метода подготовительных задач привносит в изложение доказательства некоторое своеобразие. Оно состоит главным образом в разбиении доказательства на отдельные части, что помогает лучше воспринять общий замысел рассуждений и облегчает соотнесение каждой части доказательства с выполненными ранее подготовительными заданиями.

Литература:

1. Н. М. Рогановский «Методика преподавания в средней школе», Мн., «Высшая школа», 1990г.