В данной статье приведены основные оперируемые величины, составляющие геомеханическую модель. Кратко описан принцип их определения.
Ключевые слова: геомеханическое моделирование, геомеханика, стресс, деформации, модуль Юнга, коэффициент Пуассона.
Чтобы реализовать на практике возможности геомеханики, прежде всего необходимо создать так называемую Геомеханическую Модель Земли [1]. Геомеханическая Модель Земли состоит из шести ключевых компонентов, которые могут быть как рассчитаны, так и оценены, используя полевые данные:
– Вертикальный стресс, σV (часто называемое геостатическим давлением);
– Максимальный горизонтальный стресс, σHmax;
– Минимальный горизонтальный стресс, σHmin;
– Ориентационный стресс, Azi σHmax;
– Поровое давление, Pp.
В качестве базового рабочего потока, составляющего одномерную геомеханическую модель, выступает поток с оценкой свойств горной породы. Для оценки свойств используются данные каротажей в связке с лабораторными данными по керну. Для построения профиля напряжений существуют различные эмпирические модели, в соответствии с которыми необходимо откалибровать лабораторные данные.
Давление вышележащих пород рассчитывается с помощью плотностного каротажа, поровое давление с помощью каротажей и гидродинамических исследований скважин (ГДИС), если те присутствуют.
Самая сложная часть — определение диапазона значений и азимута максимального горизонтального стресса, в этом существенную помощь оказывает измерительный прибор — микроимиджер.
Напряжения горной породы
Горная порода снаружи испытывает влияние нормальных ортогональных и сдвиговых напряжений. Нормальные напряжения ортогональны друг другу и подразделяются на: вертикальное σV— вес вышележащих пород, максимальное горизонтальное σH, минимальное горизонтальное σh. Тангенциальные напряжения стремятся развернуть участок породы.
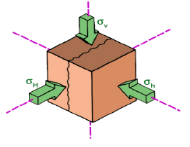
Рис. 1. Схематичное отображение основных напряжений
Напряжённое состояние можно выразить тремя основными перпендикулярными напряжениями и азимутом максимального/минимального горизонтального напряжения, избавившись от сдвиговых (тангенциальных) путём доворота осей.
Изнутри же порода оказывает воздействие на соседние участки своим поровым давлением
Рис. 2. Схематичное отображение воздействия порового давления
Деформации
Деформации подразделяются на упругие и пластичные. При упругой деформации участок, при снятии с него напряжений, восстанавливается в прежнюю форму. Пластичные же деформации откладывают на породу отпечаток в виде невосстановления в предыдущую форму и вплоть до разрушения. Например, обрушение стенок скважины вызывается влиянием сдвиговых разрушений при дисбалансе напряжений вокруг скважины.
Пластичность проявляет себя формированием микротрещин, перестройкой зёрен кристаллической решётки, формированием разломов, растворением минералов горной породы.
Опытным путём способности к деформациям определяют в лабораторных условиях, применяя одноосное и/или всестороннее сжатие/растяжение керна.
Деформации можно рассчитывать методом Мора-Кулона, графическим представлением величин напряжений деформации и слома.
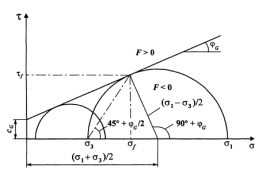
Рис. 3. Критерий Кулона-Мора: t — огибающая предельных кругов напряжений; Cg — коэффициент сцепления; φg — угол внутреннего трения; σ1 — максимальное главное напряжение; σ3 — минимальное главное напряжение; F>0 — предел прочности превышен; F<0 — предел прочности не достигнут
В расчётной части имеют значение такие величины как модуль Юнга (E) и коэффициент Пуассона (ν). Модуль Юнга (модуль продольной упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению, сжатию при упругой деформации [2]. Коэффициент Пуассона — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала [3].
Напряжённое состояние пласта
Скелет пластовой породы совместно с поровым давлением удерживают вес вышележащих пород и горизонтальные напряжения. Эффективные напряжения первым делом передаются именно на скелет. Таким образом, при увеличении эффективного напряжения, порода уплотняется, уменьшаются её фильтрационно-емкостные свойства (ФЕС).
Встречаются и зоны с аномально высоким пластовым давлением (АВПД) — недоуплотнённые зоны, образованные благодаря завышенному поровому давлению. АВПД представляют интерес в процессе разработки месторождений с точки зрения ФЕС.
Вертикальное напряжение пласта определяет собой вес вышележащих пород рассчитывается методом интегрирования плотности с глубиной. Горизонтальные же напряжения, МПа, рассчитываются сложной функцией вертикального напряжения, порового давления, модуля Юнга, коэффициента Пуассона, Биота и тектонических деформаций.
Факторы, влияющие на напряженное состояние пласта:
- Однородность и изотропность механических свойств;
- Геологическая структура;
- Разломы;
- Аномальное пластовое давление;
- Естественная трещиноватость.
Для оценки напряжённого состояния используются данные сейсморазведки (скорости волны продольная и поперечная, плотность), гамма-каротаж, пористость, глинистость, объёмный минералогический состав, анизотропия свойств породы. Ориентацию напряжений оценивают комплексом АКШ и микроимеджеров, многорычажными ориентированными каверномерами.
Затем геомеханическая модель калибруется замерами пластовых давлений и давлений разрыва пласта, закрытия трещин, данными буровых отчётов. Важную роль в калибровке играет механическое тестирование керна.
Вывод: геомеханическая модель подразумевает собой характеристики напряжённо-деформированного состояния горной породы в пластовых условиях. Составляющие модели есть: вертикальное напряжение, максимальное и минимальное горизонтальные напряжения и их ориентация, поровое давление. В результате действия этих сил и процесса разработки порода деформируется как с восстановлением, так и без вплоть до разрушения. Напряжённое состояние пласта оценивается методом корреляции сейсмо-, электро-разведки и иных с лабораторными характеристиками керна.
Литература:
- Карьера в области геомеханики. Инженерный форум. — URL: https://www.petroleumengineers.ru/blogpost/8409 (дата обращения: 16.10.2018)
- Модуль Юнга. Википедия. — URL: https://ru.wikipedia.org/wiki/Модуль_Юнга (дата обращения: 16.10.2018)
- Коэффициент Пуассона. Википедия. URL: https://ru.wikipedia.org/wiki/Коэффициент_Пуассона (дата обращения: 16.10.2018)







