Как известно, к настоящему времени предложено большое число уравнений состояния для описания свойств систем природных углеводородов. Для инженерных расчетов более удобны кубические относительно объема уравнения состояния. Их теоретической основой является знаменитое уравнение состояния Ван-дер-Ваальса. Уравнения состояния Ван-дер-Ваальсового вида выгодно отличаются от различных модификаций многокоэффициентных уравнений своей простотой и возможностью аналитического определения корней. При этом кубические уравнения состояния зачастую не только не уступают, но и превосходят эти уравнения по точности предсказания термодинамических свойств чистых веществ и их смесей. Это направление в разработке и применении уравнений состояния для моделирования фазового равновесия нефтегазоконденсатных смесей в последние годы стало доминирующим [1–5].
В работе устанавливается аналитический вид кривых, ограничивающих область двухфазного состояния (бинодаль и спинодаль). Это позволяет установить состояние фазового равновесия системы углеводородов. Знания аналитического вида уравнения кривых, характеризующих двухфазное состояние, позволяют математически решать многие задачи разработки совместно с использованием других важных уравнений в одной системе. А это, в свою очередь, повышает качество проектирования и эксплуатации нефтяных и газоконденсатных месторождений.
Ключевые слова: фазовое равновесие, прогнозирование, неравенство, объем, давления, температура, бинодаль, спинодаль.
As is known to date, a large number of state equations have been proposed for describing the properties of natural hydrocarbon systems. For engineering calculations, cubical relative to the volume of the equation of state is more convenient. Their theoretical basis is the famous Van der Waals equation of state. The equations of state of the van der Waals type favorably differ from the various modifications of the multi-coefficient equations by their simplicity and the possibility of an analytic determination of the roots. In this case, the cubic equations of state are often not only inferior, but also exceed these equations in the accuracy of predicting the thermodynamic properties of pure substances and their mixtures. This direction in the development and application of the equations of state for modeling the phase equilibrium of oil and gas condensate mixtures has become dominant in recent years [1–5].
In the paper, an analytical form of the curves that bound the region of the two-phase state (binodal and spinodal) is established. This allows us to establish the state of phase equilibrium of the hydrocarbon system. Knowledge of the analytical form of the equation of curves characterizing a two-phase state allows us to mathematically solve many development problems in conjunction with the use of other important equations in one system. And this, in turn, improves the quality of design and operation of oil and gas condensate fields.
Keywords: phase equilibrium, prediction, inequality, volume, pressure, temperature, binodal, spinodal.
К настоящему времени предложено большое число уравнений состояния для описания свойств систем природных углеводородов. В инженерной практике наиболее широкое применение нашли два вида — многокоэффициентные и кубические.
К кубическим относятся уравнения Ван-дер-Ваальса и его различные модификации.
Предположим, что уравнение состояния в наиболее общем случае имеет вид:
![]() . (1)
. (1)
После подстановки
![]() (2)
(2)
получается уравнение ![]() ,где
,где
![]() ,
, ![]() (3)
(3)
Нами было установлено, что, если уравнение ![]() имеет три действительных корня
имеет три действительных корня ![]() , то корни находятся в промежутках:
, то корни находятся в промежутках:
![]() (4)
(4)
Известно, что это возможно, когда коэффициенты р и q удовлетворяют условию ![]() ,
, ![]()
В модифицированных уравнениях Ван-дер-Ваальса, как известно, меньший корень соответствует жидкой фазе, средний — двухфазному состоянию, а больший корень –газовому. Этот факт можно использовать для нахождения зависимостей и графиков, соответствующих этим фазам. Например, для нахождении области, соответствующей двухфазному состоянию, необходимо решить уравнение ![]() (учитывая формулы (2), (3)) или
(учитывая формулы (2), (3)) или
![]() . (5)
. (5)
Как известно
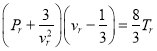 . (6)
. (6)
Если последнее написать в виде (1), то получим:
![]() (7)
(7)
Подставляя эти выражения в (5) и решая его относительно ![]() , получаем формулу:
, получаем формулу:
![]() (8)
(8)
При ![]() мы получаем формулу
мы получаем формулу
![]() (9)
(9)
график, которой называется бинодалью.
Эта формула соответствует двухфазному состоянию.
Если решить уравнение (6) относительно ![]() , то получим:
, то получим:
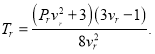 (10)
(10)
Подставляя последнее выражение в (8) и решая полученное уравнение относительно ![]() мы получаем формулу:
мы получаем формулу:
![]() (11)
(11)
График, полученный формулой (10), называется спинодалью.
Подставляя выражение (10) в (9), получаем:
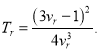 (12)
(12)
Следует отметить, что формулы (8)–(12) можно получить и другим способом. Как известно, на кривой спинодали ![]() . Если уравнение Ван-дер-Ваальса решить относительно
. Если уравнение Ван-дер-Ваальса решить относительно ![]() и найдя
и найдя 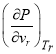 решить уравнение
решить уравнение 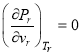 , то получим формулу (12). Подставляя ее в (6), получим формулу (11). Продолжая аналогичным образом, мы получим и все другие формулы.
, то получим формулу (12). Подставляя ее в (6), получим формулу (11). Продолжая аналогичным образом, мы получим и все другие формулы.
Для того чтобы получить формулу между ![]() и
и ![]() , представим формулу (11) в виде:
, представим формулу (11) в виде: ![]() или
или
![]() (13)
(13)
Введя обозначение ![]() и используя формулу Карно, для решения кубического уравнении (13) получаем:
и используя формулу Карно, для решения кубического уравнении (13) получаем:
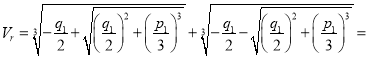 (14)
(14)
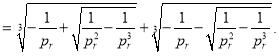
Подставляя значение ![]() из (14) в (12), получаем зависимость
из (14) в (12), получаем зависимость ![]() Все это можно сделать, не представляя уравнение Ван-дер-Ваальса в приведенном виде.
Все это можно сделать, не представляя уравнение Ван-дер-Ваальса в приведенном виде.
Действительно, решая уравнение Ван-дер-Ваальса относительно ![]() можно представить его в виде
можно представить его в виде ![]() , а затем, решая уравнение
, а затем, решая уравнение ![]() , мы получим
, мы получим 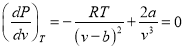 или
или
![]() . (15)
. (15)
Далее, подставляя (15) в уравнение Ван-дер-Ваальса, мы получаем:
![]() (16)
(16)
Здесь ![]() .
.
Затем, если найти зависимость между ![]() и Р из (17), подставив ее в уравнение (16), мы получим формулу
и Р из (17), подставив ее в уравнение (16), мы получим формулу ![]() .
.
С целью необходимости учета свойств многокомпонентных систем получим эти же зависимости для более сложных уравнений состояния с набором экспериментально определяемых констант. Используем, например, уравнение состояния Редлиха-Квонга, которое является модификацией уравнения Ван-дер-Ваальса:
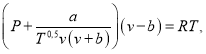 (17)
(17)
где ![]() ,
, ![]()
Решая уравнение
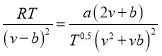 или
или
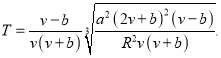 (18)
(18)
Подставляя последнее уравнение в (17), получаем формулу:
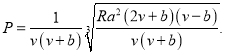 (19)
(19)
Последнее уравнение является уравнение спинодали.
А теперь решим эту задачу в наиболее общем виде:
![]() , (20)
, (20)
где b, c, d — коэффициенты, постоянные для данного вещества; коэффициент а зависит от температуры (![]() константа,
константа, ![]() — температурная функция, равная единице при критической температуре).
— температурная функция, равная единице при критической температуре).
Уравнение состояния (20) можно записать также в кубическом относительно мольного объема виде:
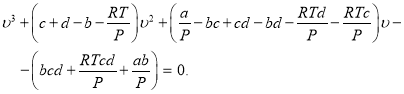 (21)
(21)
Здесь ![]()
Для расчетов коэффициентов
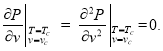 (22)
(22)
Для уравнения (20) решим уравнение ![]() откуда получаем:
откуда получаем:
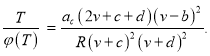 (23)
(23)
Для уравнения Соаве-Редлиха-Квонга![]()
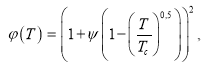 (24)
(24)
где ![]() . (25)
. (25)
Для формулы Редлиха-Квонга (RK) ![]() определяется также, однако здесь:
определяется также, однако здесь:
![]() (26)
(26)
Здесь величину ![]() можно приближенно оценить по формуле
можно приближенно оценить по формуле
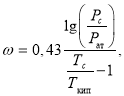 (27)
(27)
где
Учитывая (23) и (24) можно получить:
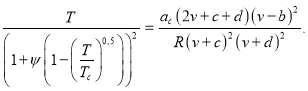 (28)
(28)
Решая последнее квадратное уравнение относительно ![]() , мы получаем зависимость
, мы получаем зависимость ![]() Далее, подставляя последнее в (20), мы получим уравнение спинодали
Далее, подставляя последнее в (20), мы получим уравнение спинодали ![]()
Таким образом, в работе устанавливается аналитический вид кривых, соответствующих двухфазному состоянию. Это позволяет установить состояние фазового равновесия системы углеводородов. Знания аналитического уравнения кривых, характеризующих двухфазное состояние, позволяют математически решить многие задачи разработки совместно с использованием других важных уравнений в одной системе. А это, в свою очередь, повышает качество проектирования и эксплуатации нефтяных и газоконденсатных месторождений.
Литература:
- Брусиловский А. И. Фазовые превращения при разработке месторождений нефти и газа. —М.: Грааль, 2002. –575 с.
- Мирзаджанзаде А. Х., Аметов И. М., Ковалев А. Г. Физика нефтяного и газового пласта. – Москва-Ижевск: Институт компьютерных исследований. — 2005. –280 с.
- Мирзаджанзаде А. Х., Кузнецов О. Л., Басниев Х. С., Алиев З. С. Основа технологии добычи газа. — М.: Недра, 2003. — 880 с.
- Гиматудинова Ш. К., Ширковский А. И. Физика нефтяного и газового пласта. — М.: Недра, 1982.
- Гуревич Г. Р., Брусиловский А. И. Справочное пособие по расчету фазового состояния и свойств газоконденсатных смесей. — М.: Недра, 1984.







