О неустановившемся режиме работы скважин с учетом влиянии инерционных сил



В статье предложены формулы для изучения нестационарного движении нефти в пористой среде при наличии влиянии инерционных сил. Для этого рассмотрены как двучленные, так и трехчленные законы фильтрации

Ключевые слова: градиент, давление, депрессия, фильтрация.

The article proposes formulas for studying the unsteady motion of oil in a porous medium in the presence of the influence of inertial forces. For this, we consider both binomial and three-term filtering laws.

Keywords: gradient, pressure, depression, filtration.

Рассмотрим уравнение для неустановившейся фильтрации жидкости при влиянии инерционных сил. Примем что закон изменения параметров пласта и жидкости в зависимости от давления имеет вид:

, (1)

При влиянии инерционных сил, т. е. когда фильтрация происходит по двучленному или же по трехчленному закону фильтрации полученная скорость при одних и тех же значениях исходных параметров будет меньше, чем по закону Дарси.

Тогда можно написать (2)

Дифференциальная уравнение такой задачи будет

(3)

где .

Эта задача эквивалентна задаче, которая решена []. В этом случае закон изменения параметров пласта и жидкости в зависимости от давления имеет вид:

(4)

Линериализация такого дифференциального уравнения имеет вид:

(5)

где

Формулы для определения изменения давлении при работе скважины с постоянным дебитом будут:

(6)

Наконец, формулы для расшифровки кривых восстановлении давления без учета притока будут иметь вид:

,(7)

, (8)

Исследования скважин на неустановившихся режимах работы подразделяются на следующие основные виды.

1. Снятие кривых восстановления забойного давления после остановки эксплуатационной или нагнетательной скважины.
2. Пьезоразведка (гидропрослушивание) пласта, при которой фиксируют влияние изменения режима работы возмущающей скважины на характер изменения давления в соседних реагирующих скважинах. Расшифровка данных почти всех видов исследования скважин основаны на решении нелинейного уравнения, полученном как первое приближение линеаризации Лейбензона. Обобщение известных в линейной теории упругого режима методов обработки материалов изучения нелинейно-упругого режима фильтрации однородной жидкости достигается путем замены в расчетных формулах давления 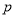на функцию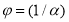 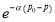, а дебит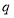а на 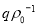. Здесь коэффициент изменения параметров 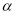предварительно определяется по данным расшифровки результатов исследования скважин на установившихся режимах, т. е. индикаторных линий. Пренебрежение сведениями о стационарном притоке к скважинам оправдано лишь в том случае, если индикаторные линии-прямые. При этом справедливы способы расшифровки результатов исследования скважин, следующие из линейной теории упругого режима фильтрации. Если индикаторная линия кривая, то необходимо прибегать к способам определения параметров пласта при нелинейно-упругом режиме фильтрации.

Как известно, двучленный закон фильтрации имеет следующий вид []:

(9)

Перепишем его в следующем виде:

(10)

где . (11)

Понятно, что при одних и тех же значениях исходных параметров скорость, полученная из двучленного закона фильтрации, будет меньше, чем по закону Дарси. Если скорость по закону Дарси обозначим через то для значения скорости фильтрации при двучленном законе фильтрации можно написать:

, (12)

где значение связано с параметрами Найдем выражение для . Так как при таком предположении выражение (12) является решением (10), то можно написать:

(13)

Известно, что при установившемся режиме фильтрации (14)

Подставляя вместо в (13), получаем:

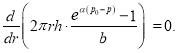(15)

Откуда

(16)

При из (2.11.13) получаем:

(17)

из (16): (18)

Разделив (17) на (18), получаем:

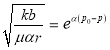или (19)

подставляя при и получаем 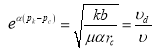. (20)

Откуда , где . (21)

С другой стороны, из (20) можно получить . (22)

Понятно, что значения, полученные по (21) и (22) должны совпадать.

Таким образом, двучленный закон фильтрации можно заменить более простой закономерностью:

Это позволяет значительно упростить математические модели, связанные с фильтрацией.

А теперь предположим, что фильтрация происходит по трехчленному закону:

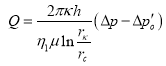. Решая это уравнение, с одной стороны, мы получим выражение для дебита []: (23)

С другой стороны, учитывая формулу (18) мы получаем для дебита 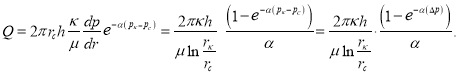(24)

Приравнивая дебиты, полученные двумя способами, имеем:

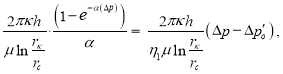(25)

где

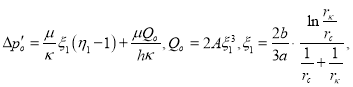
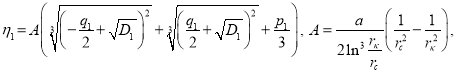
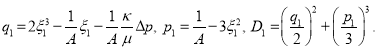(26)

Из (26) получаем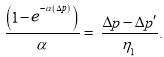 (27)

А теперь покажем, как можно найти .

Разлагая в ряд Тейлора, получаем:

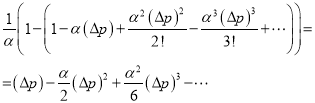
Взяв четыре члена разложения, мы в графике 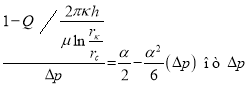по точке пересечения прямой с осью ординат получаем значение следовательно, иДля проверки правильности, учитывая, что угловой коэффициент мы сравниваем полученное значение со значением Здесь

Следует отметить, что, если влияние инерционных сил отсутствует, то 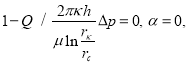т. е. мы получаем закон Дюпюи.

Таким образом определяя с помощью исследований при установившимся режиме фильтрации, можно исследовать нестационарное движении нефти в пористой среде с учетом влиянии инерционных сил.

Литература:

1. А. Х. Мирзаджанзаде, О. Л. Кузнецов, Х. С. Басниев, З. С. Алиев. Основа технологии добычи газа. — М.: Недра, 2003. –880 с.
2. А. Х. Мирзаджанзаде, И. М. Аметов, А. Г. Ковалев. Физика нефтяного и газового пласта. –Москва-Ижевск: Институт компьютерных исследований. —2005. –280 с.
3. К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. Подземная гидравлика. –М.: Недра, 1986. — 303 с.