Статья посвящена решению задачи Коммивояжера с использованием стохастического алгоритма муравьиной колонии. На основе решения данной задачи предлагается пример информационной системы для организации транспортной логистики.
Ключевые слова: алгоритм муравьиной колонии, алгоритмы оптимизации транспортных логистических процессов, транспортная логистика, системы управления транспортом.
Article devoted to solving travelling salesman problem using stochastic ant colony optimization algorithm. Based on this solution was developed transport logistic system.
Keywords: ant colony optimization algorithm, transport logistic, transport management system, transport logistics process optimization algorithms.
Транспортное направление развивается быстрыми темпами, чему способствует изменение и улучшение мировой политики, экономики и различные интеграционные процессы. Геополитика и экономика — два самых важных фактора в развитии транспортных потоков в ХХІ веке.
Для более быстрой интеграции отечественного транспортного комплекса в систему всего мира необходимо, в первую очередь, развитие транспортной логистики. Тщательное изучение мирового рынка, применение полученных знаний в отношении всевозможных грузоперевозок, а также работа с пассажирами дают свои положительные результаты. Огромный стратегический ресурс транспортного потока способен привести к повышению грузооборота, а это ведет к развитию экономики, как страны, так и мира в целом. Необходимо повышать эффективность отечественной транспортной системы — улучшать качество перевозок, обеспечивать более комфортные условия для пассажиров, выполнять все условия договоров с грузоперевозчиками и экспедиторами. Оптимизация транспортной логистики с применением новой методологии позволяет избежать нерациональных затрат. Транспортные компании стремятся к новым, современным методам работы, стараясь соответствовать всем запросам клиента. Большие надежды возложены на развитие транспорта как отечественного, так и мирового. Логистика призвана помочь улучшить финансовое благосостояние всех транспортных предприятий, поднять их рейтинг, объем перевозок и спрос на рынке.
Транспортная логистика — понятие, включающее в себя различные методы и системы организации грузовых и пассажирских перевозок. Постоянные поиски наилучшего варианта, как доставить груз в целости и сохранности с наибольшим комфортом, сокращать время пребывания в пути и избежать ненужных затрат — основные задачи транспортной логистики.
Транспортная логистика занимается решением задач, связанных с транспортировкой груза и оптимизацией всех транспортных потоков. К задачам транспортной логистики относятся все логистические процессы, относящиеся к транспортировке грузов. Главными задачами оптимизации транспортной логистики считаются: задача поиска наиболее краткого пути доставки и задача коммивояжера. Для решения NP-полной задачи коммивояжера требуются точные либо приближенные оптимизационные алгоритмы. Для решения задачи коммивояжера нужно, чтобы маршрут был оптимизирован под прохождение по определенным населенным пунктам минимум 1 раз. К условиям основной задачи относятся следующие исходные данные: данные выбора маршрута, как на дальние, так и ближние расстояния; необходимые матрицы расстояний и конечная стоимость перевозки. Самое основное условие — маршрут обязательно должен пройти по определенному населенному пункту единственный раз, чтобы результат задачи коммивояжера находился посреди гамильтоновых циклов.
Для простых методов исчисления задачи коммивояжера требуется: лексический полный разбор, методы ближнего соседа (это так называемый «жадный» алгоритм), подключения ближнего города, наиболее дешевого включения, а также остового минимального дерева. Главные модификации, которые являются весьма успешными приемами для вычисления задачи коммивояжера, это метод границ и веток, муравьиной колонии и генетических алгоритмов.
Алгоритм муравьиной колонии считается самым эффективным полиномиальным алгоритмом, он требуется, чтобы найти решение задачи коммивояжера. Основная сущность заключена в анализе и применении методов работы и поведения муравьев, которые постоянно находятся в поиске наиболее выгодного направления от формирования своей колонии к ресурсам. В основе алгоритма муравьиной колонии находится ее поведенческая реакция — это маркировка всех успешных направлений при помощи наибольшего числа феромонов. Начало работы — это расположение муравьиного феромона на вершинах графы (населенных пунктах), после этого стартует движение муравьев, его направление находят методом вероятности при помощи следующей формулы:
![]()
- — это вероятность перехода путем;
- — это длина i-ого перехода;
- — число феромонов на i-том переходе;
- — это величина, нужная для определения «жадности» алгоритма;
- — это величина, нужная для определения «стадности» і;
![]()
Полученный результат не самый оптимальный, он больше относится к неточным и наихудшим решениям. Однако в силу вероятностной природы метода, если его повторять, можно добиться наиболее точного результата.
Для улучшения современных методов вычисления задач транспортной логистики было разработано программное обеспечение, которое представляет собой веб-систему. Для работы в системе нужен администратор и водитель. Администратор занимается управлением программного обеспечения, а водитель, в свою очередь, получает необходимую ему информацию от системы. Все возможные варианты использования программного обеспечения изображены на диаграмме прецедентов (рис.1).
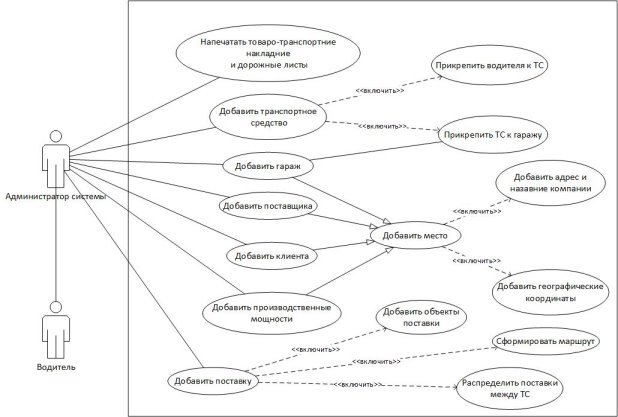
Рис. 1. Диаграмма вариантов использования
После учета всех необходимых требований можно приступать к разработке программного обеспечения. Для успешной работы без вмешательства третьих лиц, вход в веб-систему ограничен авторизацией с применением пароля (рис. 2).
Рис. 2. Страница авторизации в системе
Система требует ввода дополнительных данных для обширной работы, поэтому программистами была разработана нижеследующая таблица (рис. 3).
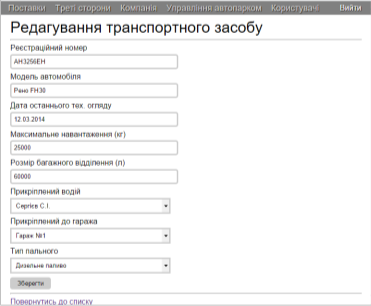
Рис. 3. Страница редактирования транспортного средства
Пристальное внимание требуется странице для работы с картами, ведь вся основная работа системы ведется на этой странице. Пример работы с добавлением нового пункта назначения приведен на рисунке 4.
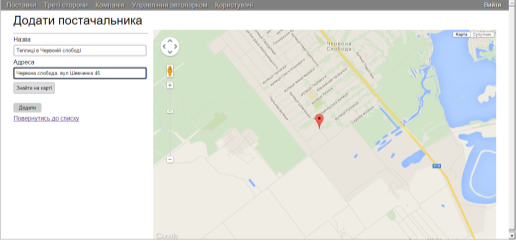
Рис. 4. Страница добавления нового пункта назначения в системе
Для построения наиболее оптимального маршрута система пользуется алгоритмом муравьиной колонии. Чтобы отобразить результаты муравьиного алгоритма, используется страница на рисунке 5.
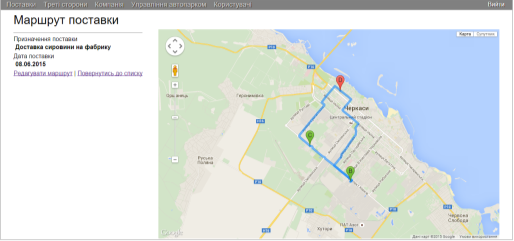
Рис. 5. Результат работы алгоритма.
Литература:
- Сокур И. М., Сокур Л. М., Герасимчук В. В. Транспортна логістика. — К.: Центр учбової літератури, 2009. — 222 с.
- Гаджинский А. М. Логистика. — 20-е изд. — М.: Издательско-торговая корпорация «Дашков и К°», 2012. — 484 с.
- Левитин А. В. Алгоритмы: Введение в разработку и анализ. — М.: Издательский дом «Вильямс», 2006. — 576 с.







