В статье исследуются вопросы геометрического анализа развязок железнодорожных линий в узлах в интерпретации гладких замкнутых кривых в 
. В работе [3] уже исследовалась взаимосвязь узловых путевых структур с гладкими вложениями окружности 
в трехмерное евклидово пространство 
, и выявлена параллель между теорией узлов и железнодорожными развязками.
В двойные точки самопересечения соответствуют проходам и переходам, указывающим, какие нити узла проходят поверху, а какие — понизу. В же исследуются простые точки самопересечения.
В статье мы обсудим основные результаты формулы Фабрициуса-Бьерре применительно к геометрическому анализу путевого развития железнодорожных развязок в разном уровне. Прежде чем изложить основную теорему Фабрициуса-Бьерре нам понадобятся некоторые определения.
Пусть 
‒ некоторая замкнутая дифференцируемая кривая в , такая, что
-
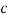состоит из конечного числа выпуклых дуг, которые не касаются друг друга, кроме точек самопересечения.
- Через каждое пересечение проходит ровно две ветви кривой (двойная точка).
Определение 1. Двойная касательная ‒ это прямая, которая касается кривой в двух различных точках.
Существуют внешние и внутренние двойные касательные (рис. 1).
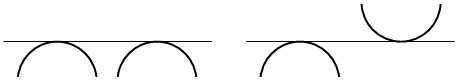
Рис. 1. Два вида двойных касательных
Определение 2. Внешняя двойная касательная является двойной касательной, в которой выпуклые дуги в окрестности точек соприкосновения находятся на одной стороне линии.
Определение 3. Внутренняя двойная касательная является двойной касательной, в которой выпуклые дуги в окрестности точек соприкосновения находятся на противоположных сторонах линии.
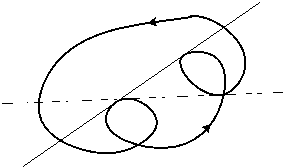
Рис. 2. Для замкнутой, дифференцируемой ориентируемой кривой в есть два пересечения и нет точек перегиба. Внешняя двойная касательная показана сплошной линией, а внутренняя — пунктирной.
Точки перегиба определяются следующим образом. При задании на плоской кривой ориентации и двигаясь по ней, мы делаем поворот либо налево, либо направо. Точки перегиба указывают изменение направления поворота на противоположное. Общее число точек перегиба замкнутой кривой четно.
Рассмотрим схему простейшей развязки двухпутных железнодорожных линий в узле. Превратим ее в плоскую замкнутую кривую путем соединения линий между собой без образования новых двойных точек самопересечения. Полученную кривую упростим, стараясь максимально избавиться от всех лишних кривых участков, то есть минимизируем число точек перегиба (рис. 3).
Рис. 3. Развязка двухпутных линий и ее упрощенная геометрическая интерпретация
Пусть 
и 
‒ число внешних и внутренних двойных касательных гладкой замкнутой кривой, 
‒ (четное) число ее точек перегиба, а 
‒ число двойных точек самопересечения. Тогда существует теорема, определяющая зависимость этих параметров между собой.
Теорема 1. Для замкнутой кривой разность между числом внешних и внутренних двойных касательных равна сумме числа пересечений и половины числа точек перегиба:
.
Для плоской кривой, представляющей развязку на рис. 3, 
, 
, 
, 
.
Данная формула открыта датским математиком Фабрициус-Бьерре в 1962 году (см. [4]). В книге [1, с. 191–193] приводится доказательство этой теоремы.
Целесообразность в совершенствовании путевых схем развязок и их реконструкция обусловлена в первую очередь увеличением размеров поездопотоков на подступах к ним в магистралях и в них самих.
Существующие методы этапного совершенствования узловых путевых структур предусматривают их реконструкционные мероприятия из существующего состояния в конечное, путем создания стратегии ступенчатых перестраиваний по критерию минимума приведенных затрат. Настоящее решение в действительности является лишь количественным увеличением элементов путевого развития развязок, а качественное обоснование этой многоплановой и многосоставной процедуры остается в тени. В работе [2] формирование такого процесса совершенствования объясняется «принципом линеаризации», то есть применением линейной системы для аппроксимации поведения решений нелинейной системы в окрестности точки равновесия.
Хотя такого рода линеаризация и способствует определению большего числа качественных и преимущественно количественных свойств системы, однако эти линейные системы обладают вполне предвидимым поведением. Данное усмотрение является ничем иным, как существенным облегчением и ориентацией на неточность представления сути явления. Таково состояние традиционного взгляда на поэтапные процессы развития путевых структур развязок в железнодорожных узлах, как сложной системы.
При необходимости совершенствования схем и обосновании их этапного развития, сами конечные результаты таких линейных систем довольно сложно предугадать, что ведет за собой невозможность разрешения вопроса о достижении желаемого конечного состояния. Наряду с этим недостатком, еще более существенной проблемой является невыполнимость оптимизационных расчетов по стратегии трансформации последовательных изменений путевых структур железнодорожных узлов из предварительного состояния в последующее и конечное.
В общем смысле процессы совершенствования путевого оснащения железнодорожных узлов протекают либо по курсу как увеличения числа их путевых элементов, так и числа элементов станционных устройств (количественный рост), либо ‒ по курсу реорганизации действующей путевой структуры. Стратегия только наращивания числа элементов узловых путевых структур влечет за собой снижение устойчивого функционирования железнодорожного узла как единой динамической системы. В результате возникают перебои в его непрерывном совершенствовании как с учетом внешних факторов, так и с учетом внутренних накладываемых ограничений.
Именно такого рода ориентация процессов развития путевых структур железнодорожных узлов прежде всего связана с сопоставлением их с классом нелинейных систем.
Литература:
- Табачников С. Л., Фукс Д. Б. Математический дивертисмент. 30 лекций по классической математике / Пер. с англ. под ред. С. М. Львовского. — 2-е изд., стереотип. — М.: МЦНМО, 2016. — 512с: ил.
- Жардемов Б. Б. Теоретические основы развития железнодорожных станций и узлов: дисс. док. техн. наук: 05.22.08. — Москва, 1999. — 410 с.: ил.
- Шмаль С. Н., Павлова Е. Ю. Эффективность применения групп кос к анализу и кодировке топологической структуры развязок железнодорожных линий разного уровня в узлах // Молодой ученый. — 2017. — № 1. — С. 129–133.
- F. Fabricius-Bjerre. On the double tangents of plane closed curves // Math. Scand. 1962. V. 11. P. 113–116.
