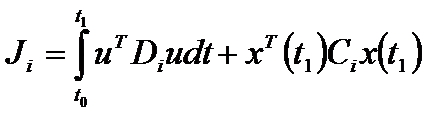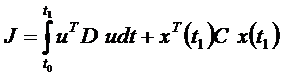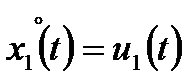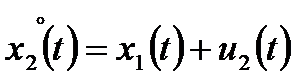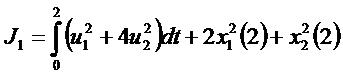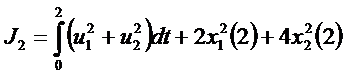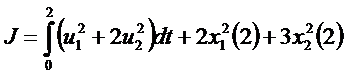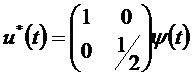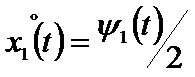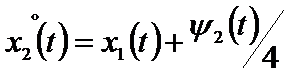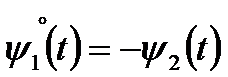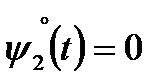Введение.
Человеку в своей деятельности для достижения поставленных целей приходится принимать решения. Задачи, связанные с выбором оптимальных решений, встречаются в экономике, технике, военном деле и т.д. По мере развития этих сфер процессы принятия решений формализуются и приобретают вид математических моделей, которые отражают проблему в абстрактной форме и позволяют учесть несколько разнообразных характеристик.
При этом на первый план выходит изучение динамических систем. При наличии нескольких критериев в динамических задачах необходимо искать разумный компромисс, который заключается в выборе такого управления, что доставляет экстремальные значения одновременно всем критериям. Например, в экономике, когда в процессе функционирования предприятия одновременно ставятся разные цели: добиться максимально возможных прибыли и выпуска, одновременно с этим выдержать установленные показатели по номенклатуре или ассортименту, снизить себестоимость, добиться определенного уровня качества и рентабельности производимой продукции и т.д. Причем, в выборе такого оптимального решения лицу, принимающего решение (ЛПР) могут помочь независимые эксперты, которые высказываются о важности представленных критериев, например, указав их весовые коэффициенты. В этом случае многокритериальная динамическая задача может быть сведена к однокритериальной. Исследованием таких задач занимается теория оптимального управления. Основы этой теории были заложены академиком Л.С. Понтрягиным, центральным результатом здесь является принцип максимума [1-3].
Очевидно, что для принятия обоснованных решений ЛПР необходимо опираться на опыт, знания и интуицию специалистов. Тем самым недостаток информации можно компенсировать формализовано представленными знаниями экспертов. Для получения и обработки подобной информации стала развиваться самостоятельная дисциплина - теория и практика экспертных оценок. Экспертные исследования проводят с целью подготовки информации для ЛПР. Для проведения работы по методу экспертных оценок создают рабочую группу, которая организует по поручению ЛПР деятельность экспертов, объединенных в экспертную комиссию. Экспертные оценки часто используются при выборе одного варианта из многих критериев или определения веса каждого критерия. Экспертные оценки бывают индивидуальные и коллективные. Существует множество методов получения экспертных оценок. В одних с каждым экспертом работают отдельно, в других экспертов собирают вместе. В одних методах число экспертов фиксировано и не изменяется со временем, в других - число экспертов растет в процессе проведения исследования, например, при использовании метода "снежного кома". Метод «Дельфи» используется для прогнозирования научно-технического развития, метод Сценариев применяется для экологического или социально-экономического экспертного прогнозирования, популярен метод Мозгового штурма, где эксперты высказывают свои идеи и, обсуждая, приходят к компромиссному решению [4].
С математической точки зрения проводить анализ мнений экспертов легче, если они имеют числовую форму, тем самым можно вывести компромиссное, согласованное мнение, которое устраивает одновременно всех экспертов. Существуют две основные шкалы измерений: количественная и качественная [5]. Наиболее часто мнения экспертов выражены в количественной шкале, т.к. эксперт может сказать, что один показатель (критерий) более важен, чем другой. В качественной шкале (порядковой шкале и шкале наименований) числа используются как метки, поэтому использование этой шкалы не целесообразно в задачах многокритериального выбора. Согласованное же мнение будем определять как среднее значение мнений всех экспертов; наиболее обоснованным в многокритериальных задачах можно считать среднее арифметическое значение экспертных оценок. При этом будем считать, что ЛПР обладает информацией о компетентности экспертов и формирует свою оценку уже по экспертам. Тем самым имеем иерархию, где сначала представлена оценка экспертов лицом, принимающим решение, затем присутствуют экспертные оценки критериев в задаче многокритериального выбора. Процесс нахождения компромиссного весового вектора критериев с учетом мнений экспертов и мнения ЛПР об экспертах представлен ниже.
Во многих задачах многокритериального выбора для принятия решений используют Метод анализа иерархий (МАИ, Analytic Hierarchy Process, AHP), предложенный Саати [6]. Этот метод представляет собой теорию, которая базируется на экспертных оценках и суждениях индивидуальных участников или групп. Число статей, в которых МАИ применяться для решения прикладных задач, в том числе и многокритериальных, превысило несколько тысяч. В России подобные исследования можно встретить в [7]. Согласно МАИ экспертами формируется матрица парных сравнений, а искомый весовой вектор (вектор приоритетов по Саати) вычисляется как собственный вектор матрицы парных сравнений, отвечающий максимальному собственному значению. Этот вектор определяет компромиссный выбор критериев в задаче принятия решений, представленный в форме весовых коэффициентов. Но МАИ не раз подвергался критике различными авторами, так как математически не обоснован способ определения весового вектора из-за нарушения свойства совместности матрицы парных сравнений. Например, Ногиным В.Д. был предложен упрощенный вариант МАИ на основе нелинейной свертки критериев, где решена проблема совместности матрицы парных сравнений [8].
В данной статье представлено решение многокритериальной динамической задачи с экспертными оценками. Многокритериальная динамическая задача имеет стандартную форму [1-3]. Экспертные оценки определяют матрицу, каждая строка которой есть мнение эксперта, представленное в виде весовых коэффициентов критериев динамической задачи. Также имеется мнение ЛПР об экспертах – вектор с коэффициентами важности (компетентности) экспертов при оценивании критериев рассматриваемой задачи. Сначала необходимо найти нормированный весовой вектор критериев, который учитывает как мнения экспертов, так и мнение ЛПР об экспертах. Затем проводиться линейная свертка критериев, относительно весового вектора, и решается задача оптимального управления с одним критерием.
Постановка и решение задачи.
Рассматривается многокритериальная динамическая задача с экспертными оценками
(1)
Аналогичные задачи рассматриваются в [2]. Здесь - управляемая динамическая система, которая описывается системой линейных дифференциальных уравнений и начальными условиями
, (2)
, (3)
где 
и 
- матрицы размера 
и 
соответственно. Через 
обозначено множество управлений, выбором которых распоряжается ЛПР. Пусть на управление ограничений не наложено, т.е. 
. Здесь 
- промежуток времени функционирования системы, где 
и 
- моменты начала и окончания процесса соответственно. В (2)-(3) представлено изменение фазового вектора 
под воздействием управления. Начальное условие 
задано и определяет начальное состояние системы.
Имеем множество критериев динамической задачи:
,
(4)
где 
и 
- положительно определенные симметрические матрицы размера 
и 
соответственно [9].
Экспертам, независимо друг от друга, для сравнения по весу или важности предлагается набор критериев
; они выступают в качестве сравниваемых объектов. Тем самым формируется неотрицательная матрица экспертных оценок
, где каждая 
-ая строка указывает на мнение 
-го эксперта в виде коэффициентов важности критериев (4) в задаче (1). Например, матрица 
говорит о том, что первый эксперт (первая строка) считает, что критерий 
является менее важным, чем критерий 
в отношении
; т.е. вес критерия 
составляет
, а критерия 
- 
. Второй эксперт также отдает предпочтение второму критерию, но уже в отношении
.
Лицо, принимающее решение, дает оценку экспертам, например, учитывая их компетентность или важность при оценивании критериев в рассматриваемой задачи. Так определяется диагональная матрица
, элементы на главной диагонали которого положительны и указывают на важность (или «вес») экспертов при оценивании критериев. Например, матрица 
говорит о том, что мнение второго эксперта в два раза считается более важным, чем мнение первого.
Задача нахождения компромиссного решения, где учитывается как мнение всех экспертов, так и ЛПР об экспертах сводится к нахождению весового вектора
. Очевидно, что такой вектор, должен быть получены из матрицы экспертов 
и матрицы
, которая дает мнение ЛПР:
, (5)
где 
- есть вектор-строка, состоящий из 
- единиц. Например, при 
вектор
. Вектор 
определяет среднее арифметической значение весов в матрице 
по критериям с учетом мнения ЛПР об экспертах, выраженное матрицей
. Элементы 
весового вектора можно нормировать, поэтому пусть вектор 
такой, что
.
Применение данного метода нахождения вектора компромиссных экспертных оценок 
к решению многокритериальной динамической задачи основано на её скаляризации при помощи линейной свертки критериев. А именно, наилучшем решением задачи (1) объявляется то, которое доставляет, возможно, меньшее значение линейной свертке критериев
. Применение МАИ к решению многокритериальных задач на основе линейной свертке критериев обосновано в [5,8].
На содержательном уровне в многокритериальной динамической задаче ЛПР, учитывая мнение экспертов и свое мнение об экспертах, выбирает такую стратегию
, которая доставляет, возможно, меньшие значения сразу всем критериям (4). Оптимальная пара 
находится как решение задачи (1).
Полученную многокритериальную динамическую задачу (1) необходимо свести к задаче оптимального управления (2)-(3) с функционалом качества
, (6)
где вид матриц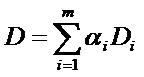 
и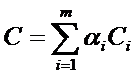 
учитывает мнение экспертов и ЛПР.
Решение задачи вида (2), (3), (6) подробно рассмотрены в [2, с.336 - 338].
Для его нахождения, воспользуемся алгоритмом применения принципа максимума Понтрягина, который является необходимым условием экстремума функционала (6).
- Составляем гамильтониан:
- Находим максимум гамильтониана по управлению. Так как ограничения на управление отсутствуют, можно применить необходимые условия безусловного экстремума:
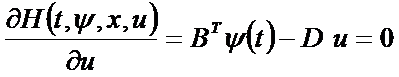
Отсюда находим вид оптимального управления:
(7)
Найденное управление обеспечивает максимум функции Гамильтона по управлению, так как удовлетворяет достаточным условием максимума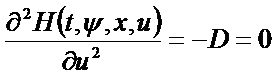 
в силу положительной определенности матрицы
.
- Выписываем уравнение системы с учетом (7) и условий трансверсальности:
, 
, (8)
, 
.
Таким образом, задача нахождения оптимального управления сводится к решению двухточечной краевой задачи для системы дифференциальных уравнений (8).
Модельный пример.
Рассматривается двухкритериальная динамическая задача с двумя экспертными оценками и мнением ЛПР о компетентности экспертов. Динамическая управляемая система, представлена дифференциальными уравнениями и начальными условиями
, 
, (9)
, 
Здесь
, 
,
. Заданы функционалы-критерии
, (10)
. (11)
Имеем оценку критериев экспертами, представленную матрицей
. Оценка ЛПР относительно экспертов имеет вид
. Тогда из выражения (5) находим вектор согласования мнений экспертов и ЛПР: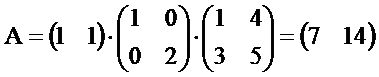 
. Нормированный вектор весовых коэффициентов для критериев (10) и (11) с учетом экспертных оценок и мнения ЛПР примет вид:
. (12)
На содержательном уровне цель ЛПР состоит в выборе такого управления
, что доставляет, возможно, меньшее значение одновременно двум функционалам (10) и (11) с учетом экспертных оценок (12). Сводим полученную многокритериальную задачу к задаче оптимального управления (2), (3) и (6).
Здесь матрицы
, 
, 
,
. Целевая функция (6) примет вид:
(13)
Используя принцип максимума Понтрягина, рассмотренный выше, находим вид оптимального управления (7)
. (14)
Имеем систему дифференциальных уравнений с краевыми условиями (8):
, 
,
, 
,
, 
,
,
.
Решением этой двухточечной краевой задачи является:
,
,
,
.
Учитывая (12) находим вектор оптимального управления
, где
,
.
Значение функционалов качества (10) и (11) с учетом экспертных оценок (12):
,
.
Заключение.
В работе рассматриваются вопросы, связанные с выбором решений при наличии нескольких критериев. А именно, представлено решение многокритериальной динамической задачи с экспертными оценками. Экспертные оценки представляют собой количественную информацию об относительной важности критериев задачи. Такой же информацией обладает лицо, принимающее решение, высказывая мнение о компетентности экспертов. Оценки экспертов и ЛПР образуют иерархию, поиск весового компромиссного вектора подробно рассматривались в работах Саати (Метод анализа иерархий) и его последователей.
Здесь развивается оригинальный подход к решению многокритериальных задач при наличии количественной информации об относительной важности, как критериев, так и экспертов. Количество экспертов, а также их оценки могут меняться со временем. В этом случае нахождения весового компромиссного вектора, отражающего как мнение экспертов, так и мнение ЛПР, проводится линейная свертка критериев и решается задача оптимального управления стандартным способом, использую принцип максимума Понтрягина. Используя лишь конечный набор информации об относительной важности критериев и экспертов, можно найти единственное решение многокритериальной задачи
В статье представлен модельный пример двухкритериальной динамической задачи с двумя экспертными оценками и мнением ЛПР об относительной важности экспертов. Найдено в явном виде оптимальное управление 
и определены значения соответствующих критериев.
Литература:
- Габасов Р., Кириллова Ф.М. Основы динамического программирования. Минск., Издательство БГУ, 1975.
- Пантелеев А.В., Бортаковский А.С. Теория управления в примерах и задачах. М.: Высшая школа, 2003.
- Жуковский В.И. Кооперативные игры при неопределенности и их приложения. М: Эдиториал УРСС, 1999.
- Орлов А.И. Экспертные оценки. Учебное пособие. - М.: 2002.
- Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. – М.: ФИЗМАТЛИТ, 2002.
- Саати Т.Л. Принятие решений при зависимостях и обратных связях: Аналитические сети. – М.: Издательство ЛКИ, 2008.
- Андрейчиков А.В., Андрейчикова О.Н. Анализ, синтез, планирование решений в экономике. – М.: Финансы и статистика, 2001.
- Ногин В.Д. Упрощенный вариант метода анализа иерархий на основе нелинейной свертки критериев// ЖВМиМФ, 2004, т. 44, № 7, С. 1259-1268.
- Гантмахер Ф.Р. Теория матриц. М.: Наука, 1967. 576 c.
