В статье проводится краткий обзор и сравнительный анализ трёх динамических сред: Живая математика, Математический конструктор, GeoGebra; выделяются их преимущества и имеющиеся недостатки.
Ключевые слова: динамическая среда, Живая математика, Математический конструктор, GeoGebra
Перед началом использования в своей практической деятельности различных интерактивных и динамических сред учитель оказывается перед выбором этой среды. Под динамической средой будем понимать программу, позволяющую создавать динамические компьютерные чертежи и модели, исходные данные которых можно изменять, не влияя на весь алгоритм построения, а также просматривать их и работать с ними.
Сегодня наиболее популярными и распространёнными среди преподавателей программами динамической геометрии, на наш взгляд, являются Живая математика, Математический конструктор (МК) и GeoGebra. Проведём краткий обзор и сравнительный анализ каждой из этих сред, выделим их преимущества и имеющиеся недостатки.
Живая математика представляет собой среду моделирования и динамического преобразования чертежей, графиков и других объектов; позволяет решать широкий круг задач при изучении геометрии, алгебры, тригонометрии и математического анализа. Сформирована на основе программы Geometry’s Sketchpad v.4[1], переведена на русский язык и адаптирована Институтом новых технологий; может быть установлена на операционные системы (ОС): Windows, MacOS. Эта динамическая среда не является свободно распространяемым программным обеспечением (ПО): лицензия на одно рабочее место составляет 5 050 рублей[2]. Существует бесплатная демоверсия программы (устанавливается сроком на 10 дней), однако её минусом является возможность установки только на компьютер с операционной системой Windows.
Живая математика имеет полный набор возможностей для выполнения построений на плоскости, их преобразований и дальнейшей работы с ними, то есть практически полностью охватывает планиметрический материал. Предлагаемые создателями программы методические рекомендации это подтверждают — работе на плоскости посвящена большая часть предлагаемых материалов: от элементарных построений (точка, прямая, луч, отрезок, простейшие фигуры и пр.) до построения довольно сложных моделей, которые в той или иной степени можно использовать для наглядной демонстрации при доказательстве некоторых теорем из курса геометрии за 7–9 класс.
Что касается работы со стереочертежами, то возможности Живой математики довольно узки и специфичны. В среде отсутствует 3D-полотно, что, на первый взгляд, делает невозможными построение пространственных фигур и работу с ними. Тем не менее, построить объёмное тело (тело вращения и пр.), динамически изменяемое, всё-таки можно. Однако это построение будет довольно трудоёмким и времязатратным. Опишем этот процесс. Для создания объёмного тела нужно провести дополнительные построения, которые затем можно скрыть. Подробно останавливаться на описании данного подготовительного процесса не будем, лишь покажем, какой объём подготовительной работы необходимо проделать для начала работы со стереочертежом. На рисунке 1 показаны все дополнительные построения для задания системы координат и 3D-полотна.
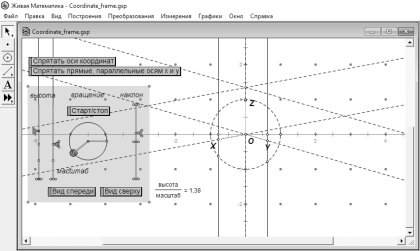
Рис. 1. 3D-полотно в среде Живая математика
Чтобы построить точку в заданной системе координат, необходимо создать числовые параметры, равные координатам данной точки, после чего применить к ним инструмент Точка по координатам. Задав точки-вершины будущего пространственного тела, нужно соединить их отрезками.
Такой подход нам кажется неуместным, поскольку привязка к системе координат и выполнение построений по координатам не всегда точны и удобны в работе. Кроме того, изменения положения тела с помощью описанных выше шкал, также является неудобным.
Математический конструктор представляет собой российскую разработку в области интерактивных динамических сред для образования. Разработчик программы — фирма 1С, которая, начиная с 1996 года, занимается созданием образовательных мультимедийных продуктов. Программа позволяет создавать интерактивные модели, объединяющие конструирование, динамическое варьирование, эксперимент, и может быть использована на всех этапах математического образования.
Среда Математический конструктор не является свободно распространяемым ПО: стоимость лицензии составляет 980 рублей[3] (одну лицензию можно использовать для установки программного обеспечения на неограниченное число устройств). Возможность установки на ОС: Windows, Linux, MacOS, IOS, Android. Также есть возможность работать в среде онлайн — на сайте производителя, однако возможности онлайн-версии продукта довольно ограничены.
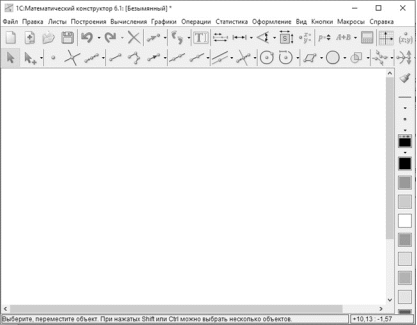
Рис. 2. Рабочее окно среды Математический конструктор
Как и предыдущая среда, МК, на наш взгляд, больше приспособлен для работы с плоскими объектами. И её возможности в этой области довольно широки — динамические геометрические построения, измерения и вычисления, функции и графики, создание заданий с автоматизированной проверкой и т. д.
В целом, интерфейс среды несложен и интуитивно понятен. Имеется необходимый набор инструментов для выполнения построений. На рисунке 2 представлено рабочее окно МК версии 6.1. В верхней части расположена панель инструментов, в правой части — элементы дизайна (позволяют выбрать цвет и стиль для построений), основную часть занимает рабочее поле (полотно).
Программа МК позволяет создавать и изменять интерактивные чертежи и модели, которые объединяют конструирование, динамическое варьирование, эксперименты, и может быть использована на всех этапах математического образования и, кроме того, в проектной деятельности учащихся.
Однако возможности этой программы для работы с пространственными объектами и стереочертежами ограничены. В ней отсутствует интерактивное 3D-полотно. Возможности работы со стереометрическими объектами пользователь может обеспечить самостоятельно.
GeoGebra[4] является динамическим программным обеспечением, визуализирующим связь между алгеброй, которая изучает буквенно-числовые выражения и равенства и неравенства этих выражений, и геометрией, которая, в свою очередь, изучает фигуры, их свойства, взаимное расположение относительно друг друга и других объектов на плоскости или в пространстве, взаимопревращения и т. д.
Разработана Маркусом Хоэнвартером (Markus Hohenwarter) австрийским математиком и профессором Университета Йоханнеса Кеплера (JKU) в Линце. Начиная с 2002 года, программа практически ежегодно завоёвывает множество образовательных наград в Европе и в США [2].
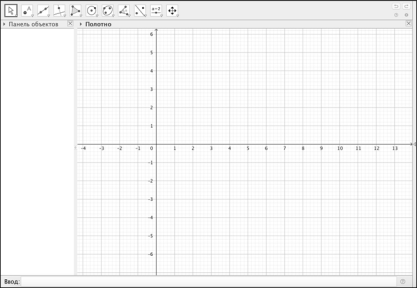
Рис. 3. Рабочее окно среды GeoGebra
Среда GeoGebra распространяется бесплатно, что позволяет беспрепятственно устанавливать её на ПК дома и в школах. Она имеет удобный и эргономичный[5] интерфейс, переведена на многие языки мира; является кроссплатформенной, то есть может быть установлена на различные операционные системы, такие как Windows, Linux, MacOS. Кроме того, есть возможность установить программу на смартфоны и планшеты, работающие под управлением операционных систем iOS и Android OS, а при необходимости — работать онлайн на сайте. На рисунке 3 представлено рабочее окно среды GeoGebra.
С одной стороны, GeoGebra представляет собой интерактивную систему геометрии. Пользователь может сделать конструкции точек, векторов, отрезков, прямых, многоугольников и конических сечений, а также функции и их динамические изменения.
С другой стороны, уравнения и координаты могут быть введены непосредственно. Таким образом, GeoGebra может работать с переменными чисел, векторов и точек, есть возможность находить производные и интегралы от функций и пр.
На основе проведённого выше анализа трёх динамических сред математического моделирования, на наш взгляд, наиболее удобной для работы учителя представляется среда GeoGebra.
Литература:
- Живая математика. Сборник методических материалов. — М.: Институт Новых Технологий. — 176 с.
- Сайт среды GeoGebra [Электронный ресурс] URL: https://www.geogebra.org/about (дата обращения: 10.08.2018)
- Сайт среды Математический конструктор [Электронный ресурс] URL: http://obr.1c.ru/mathkit/ (дата обращения: 10.08.2018)
- Фунтиков Р. А. Построение эллипса, гиперболы и параболы как конических сечений и линий плоскости в динамической среде GeoGebra. Курсовая работа. М: МПГУ, 2017. — 33 с.
[1] Разработана в 1963 году фирмой Key Curriculum Press (USA).
[2] Информация взята на официальном сайте производителя математической среды Живая математика – Институт Новых Технологи и представлена по состоянию на 10 августа 2018г.
[3] Информация взята на официальном сайте производителя математической среды Математический конструктор – 1C.Образовательные программы и представлена по состоянию на 10 августа 2018г.
[4] От первых и последних букв соответственно в словах GEOmetry и alGEBRA.
[5] Эффективный в использовании, подходящий.







